Gravitational Potential Gradient (HL) | HL IB Physics Revision Notes 2025

Gravitational Potential Gradient

A gravitational field can be defined in terms of the variation of gravitational potential at different points in the field:

The gravitational field at a particular point is equal to the negative gradient of a potential-distance graph at that point

The potential gradient is defined by the equipotential lines
- These demonstrate the gravitational potential in a gravitational field and are always drawn perpendicular to the field lines

The rate of change of gravitational potential with respect to displacement in the direction of the field

Gravitational field strength, g and the gravitational potential, V can be graphically represented against the distance from the centre of a planet, r

g = - \frac{∆ V_{g}}{∆ r}

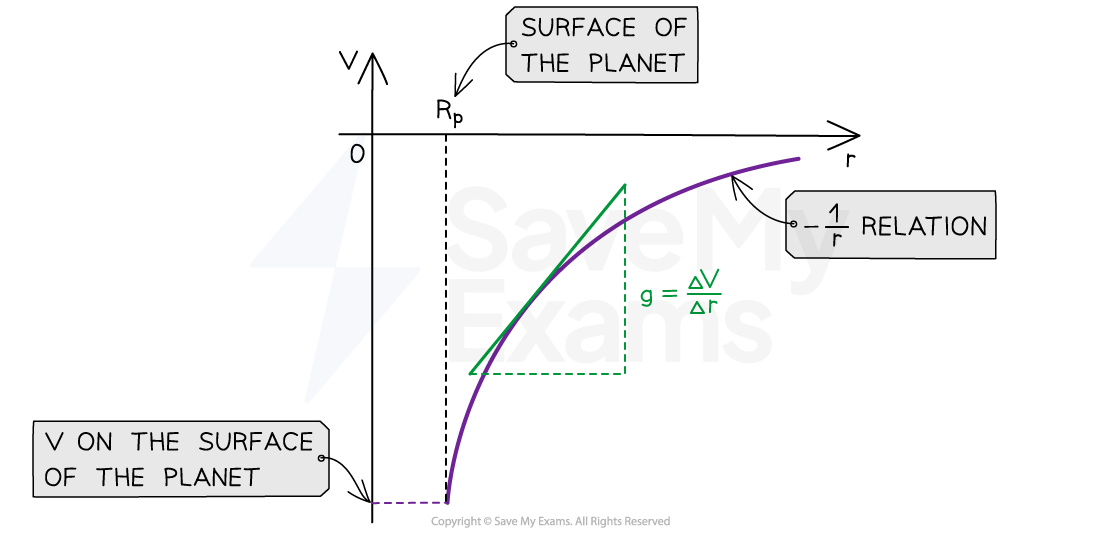
7BStox9R_7-2-3-gravitational-potential-and-distance-graph

The gravitational potential and distance graphs follow a -1/r relation

The key features of this graph are:
- The values for V_g are all negative (because the graph is drawn below the horizontal r axis)
- As r increases, V_g against r follows a $- \frac{1}{r}$ relation
- The gradient of the graph at any particular point is the value of g at that point, $g = - V_{g} \times - \frac{1}{r} = \frac{V_{g}}{r}$
- The graph has a shallow increase as r increases

To calculate g, draw a tangent to the graph at that point and calculate the gradient of the tangent
This is a graphical representation of the gravitational potential equation:

$V_{g} = - \frac{G M}{r}$

where G and M are constant

Determine the change in gravitational potential when travelling from 3 Earth radii (from Earth’s centre) to the surface of the Earth.

Take the mass of the Earth to be 5.97 × 10²⁴kg and the radius of the Earth to be 6.38 × 10⁶ m.

Answer:

Step 1: List the known quantities

Step 2: Write down the equation for potential difference

$∆ V_{g} = - G M_{E} (\frac{1}{r_{2}} - \frac{1}{r_{1}})$

Step 3: Substitute the values into the equation

$Δ V_{g} = - (6.67 \times 10^{- 11}) \times (5.97 \times 10^{24}) \times (\frac{1}{6.38 \times 10^{6}} - \frac{1}{1.914 \times 10^{7}})$

ΔV_g = −4.16 × 10⁷ J kg⁻¹