Gravitational Potential Energy Equation (HL) | HL IB Physics Revision Notes 2025

Work Done on a Mass

When a mass is moved against the force of gravity, work is required
- This is because gravity is attractive, therefore, energy is needed to work against this attractive force

The work done in moving a mass m is given by:

∆ W = m ∆ V_{g}

Where:

ΔW = change in work done (J)
m = mass (kg)
ΔV_g = change in gravitational potential (J kg⁻¹)

Worked example

A particle of mass 50 g is moved vertically from point A to point B, as shown in the diagram.

Take the gravitational field strength to be 10 N kg⁻¹.

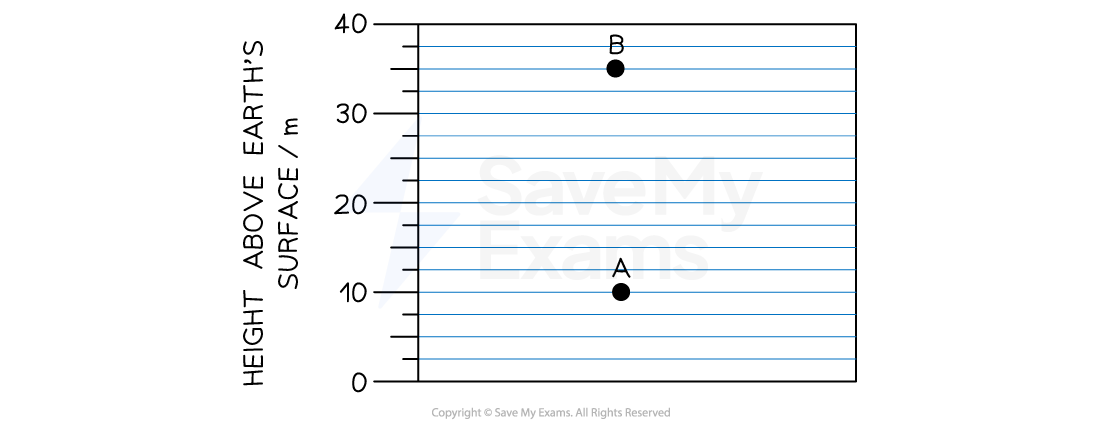
4-1-6-work-done-moving-a-mass

Determine

(a)

the potential difference between A and B

(b)

the work done in moving the mass from A to B

Answer:

(a)

The work done in moving a mass in a gravitational field is:

$W = m ∆ V$ and $W = m g ∆ h$ (close to the Earth's surface)

$m ∆ V = m g ∆ h \Rightarrow ∆ V = g ∆ h$

Where the change in height is $∆ h$ = 35 − 10 = 25 m
Therefore, the potential difference between A and B is:

$∆ V = 10 \times 25 = 250 J {kg}^{- 1}$

(b)

The work done in moving the mass from A to B is:

$W = m ∆ V$

$W = (50 \times 10^{- 3}) \times 250 = 12.5 J$

Gravitational Potential Energy Equation

In a radial field, gravitational potential energy (GPE) describes the energy an object possesses due to its position in a gravitational field

The gravitational potential energy of a system is defined as:

The work done to assemble the system from infinite separation of the components of the system

Similarly, the gravitational potential energy of a point mass is defined as:

The work done in bringing a mass from infinity to a point

The equation for GPE of two point masses m and M at a distance r is:

$E_{p} = - \frac{G m_{1} m_{2}}{r}$

Where:
- G = universal gravitational constant (N m² kg^–²)
- m₁ = larger mass producing the field (kg)
- m₂ = mass moving within the field of M (kg)
- r = distance between the centre of m and M (m)

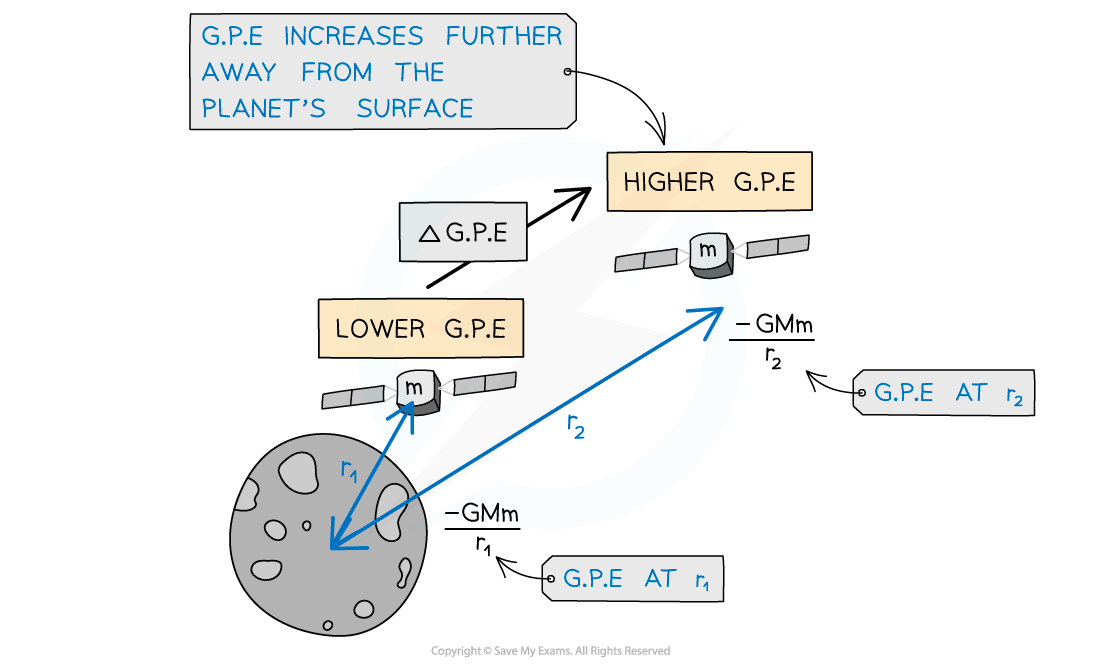
Change in GPE, downloadable AS & A Level Physics revision notes

Gravitational potential energy increases as a satellite leaves the surface of the Moon (of mass M)

Recall that Newton's Law of Gravitation relates the magnitude of the force F between two masses M and m:

$F = \frac{G m_{1} m_{2}}{r^{2}}$

Therefore, a force-distance graph would be a curve, because F is inversely proportional to r², or:

$F \propto \frac{1}{r^{2}}$

The product of force and distance is equal to work done (or energy transferred)
Therefore, the area under the force-distance graph for gravitational fields is equal to the work done
- In the case of a mass m moving further away from a mass M, the potential increases
- Since gravity is attractive, this requires work to be done on the mass m
- The area between two points under the force-distance curve, therefore, gives the change in gravitational potential energy of mass m

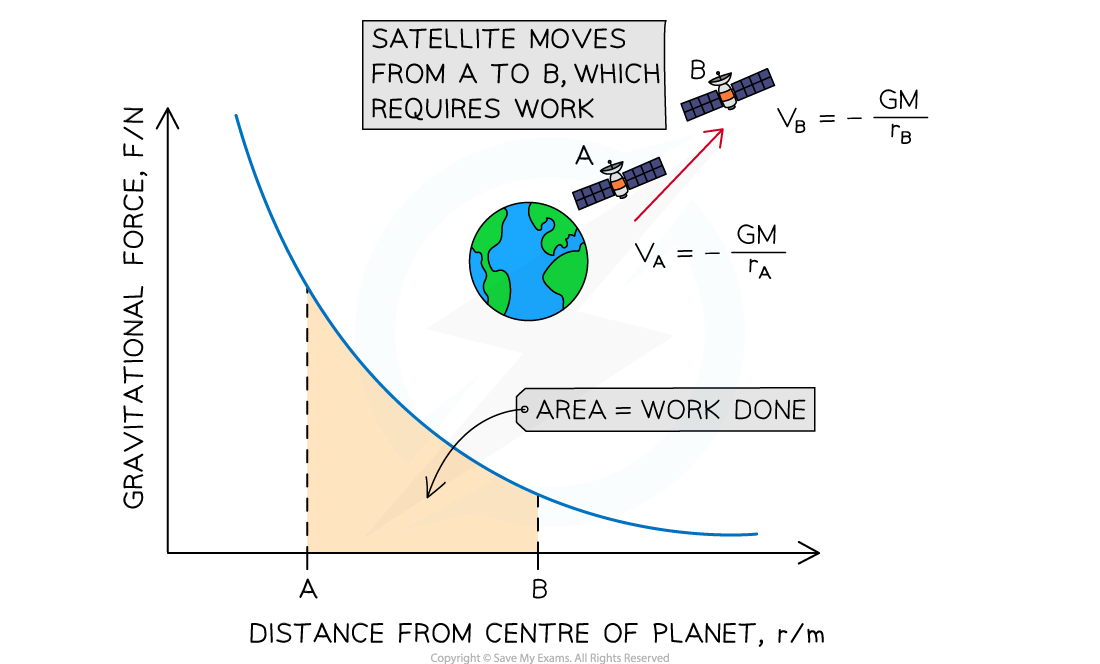
Work is done on the satellite of mass m to move it from A to B, because gravity is attractive. The area under the curve represents the magnitude of energy transferred

Change in Gravitational Potential Energy

Two points at different distances from a mass will have different gravitational potentials
- This is because the gravitational potential increases with distance from a mass
Therefore, there will be a gravitational potential difference ΔV between the two points

$∆ V = V_{f} - V_{i}$

Where:
- $V_{i}$ = initial gravitational potential (J kg^–1)
- $V_{f}$ = final gravitational potential (J kg^–1)

The change in work done against a gravitational field is equal to the change in gravitational potential energy (GPE)
- When V = 0, then the GPE = 0

It is usually more useful to find the change in the GPE of a system
- For example, a satellite lifted into space from the Earth’s surface

The change in GPE when a mass moves towards, or away from, another mass is given by:

$∆ E_{p} = - \frac{G m_{1} m_{2}}{r_{2}} - (- \frac{G m_{1} m_{2}}{r_{1}})$

$∆ E_{p} = G m_{1} m_{2} (\frac{1}{r_{1}} - \frac{1}{r_{2}})$

Where:
- m₁ = mass that is producing the gravitational field (e.g. a planet) (kg)
- m₂ = mass that is moving in the gravitational field (e.g. a satellite) (kg)
- r₁ = first distance of m from the centre of M (m)
- r₂ = second distance of m from the centre of M (m)

The change in potential ΔV_g is the same, without the mass of the object m₂:

$∆ V_{g} = - \frac{G m_{1}}{r_{2}} - (- \frac{G m_{1}}{r_{1}})$

$∆ V_{g} = G m_{1} (\frac{1}{r_{1}} - \frac{1}{r_{2}})$

Work is done when an object in a planet's gravitational field moves against the gravitational field lines i.e. away from the planet

Worked example

A spacecraft of mass 300 kg leaves the surface of Mars up to an altitude of 700 km.

Calculate the work done by the spacecraft.

Radius of Mars = 3400 km
Mass of Mars, m₁ = 6.40 × 10²³kg

Answer:

The change in GPE is equal to

∆ E_{p} = G m_{1} m_{2} (\frac{1}{r_{1}} - \frac{1}{r_{2}})

Where
- r₁ = radius of Mars = 3400 km
- r₂ = radius + altitude = 3400 + 700 = 4100 km

∆ E_{p} = (6.67 \times 10^{- 11}) \times (6.40 \times 10^{23}) \times 300 \times (\frac{1}{3400 \times 10^{3}} - \frac{1}{4100 \times 10^{3}})

Work done by satellite:

∆ E_{p} = 643.1 \times 10^{6} = 640 MJ

(2 s.f.)

Worked example

A satellite of mass 1450 kg moves from an orbit of 980 km above the Earth’s surface to a lower orbit of 480 km.

Calculate the change in gravitational potential energy of the satellite.

Mass of the Earth = 5.97 × 10²⁴ kg
Radius of the Earth = 6.38 × 10⁶ m

Answer:

Step 1: Write down the known quantities

Initial height above Earth’s surface, h₁ = 980 km
Final height above Earth’s surface, h₂ = 480 km
Mass of the satellite, m₁ = 1450 kg
Mass of the Earth, m₂ = 5.97 × 10²⁴kg
Radius of the Earth, R = 6.38 × 10⁶ m

Step 2: Write down the equation for change in gravitational potential energy

$∆ E_{p} = G m_{1} m_{2} (\frac{1}{r_{1}} - \frac{1}{r_{2}})$

Step 3: Convert distances into standard units and include Earth radius

Distance from centre of Earth to higher orbit:

$r_{1} = h_{1} + R$

$r_{1}$ = (980 × 10³) + (6.38 × 10⁶) = 7.36 × 10⁶ m

Distance from centre of Earth to lower orbit:

$r_{2} = h_{2} + R$

$r_{2}$ = (480 × 10³) + (6.38 × 10⁶) = 6.86 × 10⁶ m

Step 4: Substitute values into the equation

$∆ E_{p} = (6.67 \times 10^{- 11}) \times (5.97 \times 10^{24}) \times 1450 \times (\frac{1}{7.36 \times 10^{6}} - \frac{1}{6.86 \times 10^{6}})$

Change in gravitational potential energy: ΔE_p = 5.72 × 10⁹ J

Examiner Tip

Make sure to not confuse the ΔE_p equation with ΔE = mgΔh, they look similar but refer to quite different situations.

The more familiar equation is only relevant for an object lifted in a uniform gravitational field, meaning very close to the Earth’s surface, where we can model the field as uniform.

The new equation for E_p does not include g. The gravitational field strength, which is different on different planets, does not remain constant as the distance from the surface increases. Gravitational field strength falls away according to the inverse square law.

The change in gravitational potential energy is the work done.

Gravitational Potential Energy Equation (HL) (HL IB Physics)

Revision Note

Work Done on a Mass

Worked example

Gravitational Potential Energy Equation

Change in Gravitational Potential Energy

Worked example

Worked example

Examiner Tip

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Katie M