Gravitational Potential (DP IB Physics): Revision Note

Gravitational Potential

• The gravitational potential V at a point can, therefore, be defined as:

  The work done per unit mass in bringing a test mass from infinity to a defined point

• Gravitational potential is measured in J kg⁻¹

• It is always has a negative value because:

  • It is defined as having a value of zero at infinity

  • Since the gravitational force is attractive, work must be done on a mass to reach infinity

• On the surface of a mass (such as a planet), gravitational potential has a negative value

  • The value becomes less negative, i.e. it increases, with distance from that mass

• Work has to be done against the gravitational pull of the planet to take a unit mass away from the planet

• The gravitational potential at a point depends on:

  • The mass of the object

  • The distance from the centre of mass of the object to the point

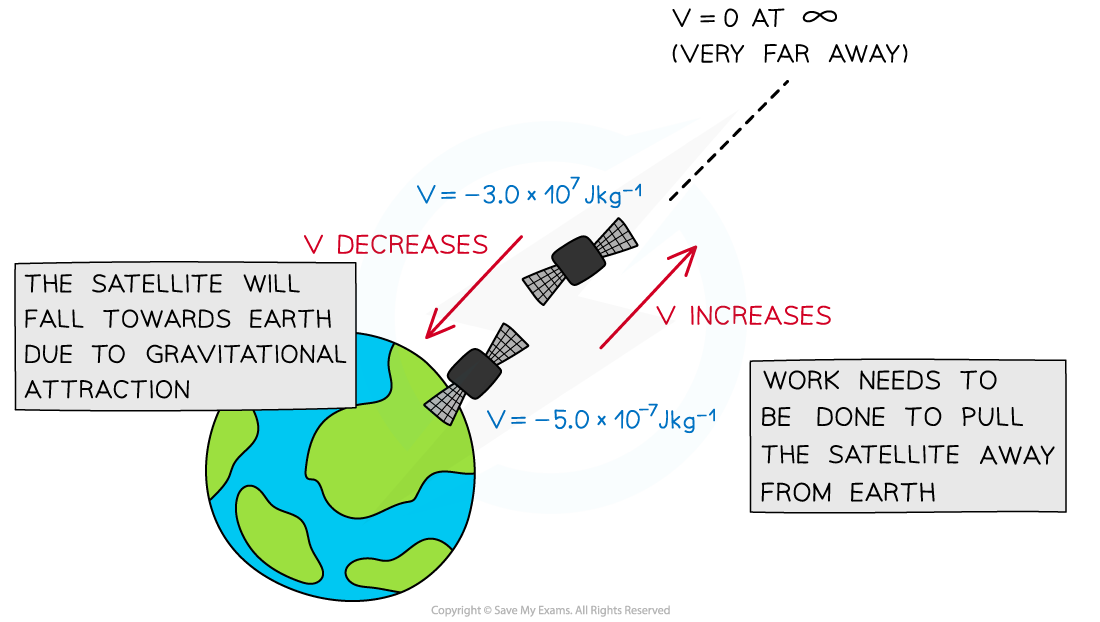
Gravitational potential decreases as the satellite moves closer to the Earth

Calculating Gravitational Potential

• The equation for gravitational potential V is defined by the mass M and distance r:

• Where:

  • V_g = gravitational potential (J kg⁻¹)

  • G = Newton’s gravitational constant

  • M = mass of the body producing the gravitational field (kg)

  • r = distance from the centre of the mass to the point mass (m)

• The gravitational potential always is negative near an isolated mass, such as a planet, because:

  • The potential when r is at infinity (∞) is defined as zero

  • Work must be done to move a mass away from a planet (V becomes less negative)

• It is also a scalar quantity, unlike the gravitational field strength which is a vector quantity

• Gravitational forces are always attractive, this means as r decreases, positive work is done by the mass when moving from infinity to that point

  • When a mass is closer to a planet, its gravitational potential becomes smaller (more negative)

  • As a mass moves away from a planet, its gravitational potential becomes larger (less negative) until it reaches 0 at infinity

• This means when the distance r becomes very large, the gravitational force tends rapidly towards zero the further away the point is from a planet

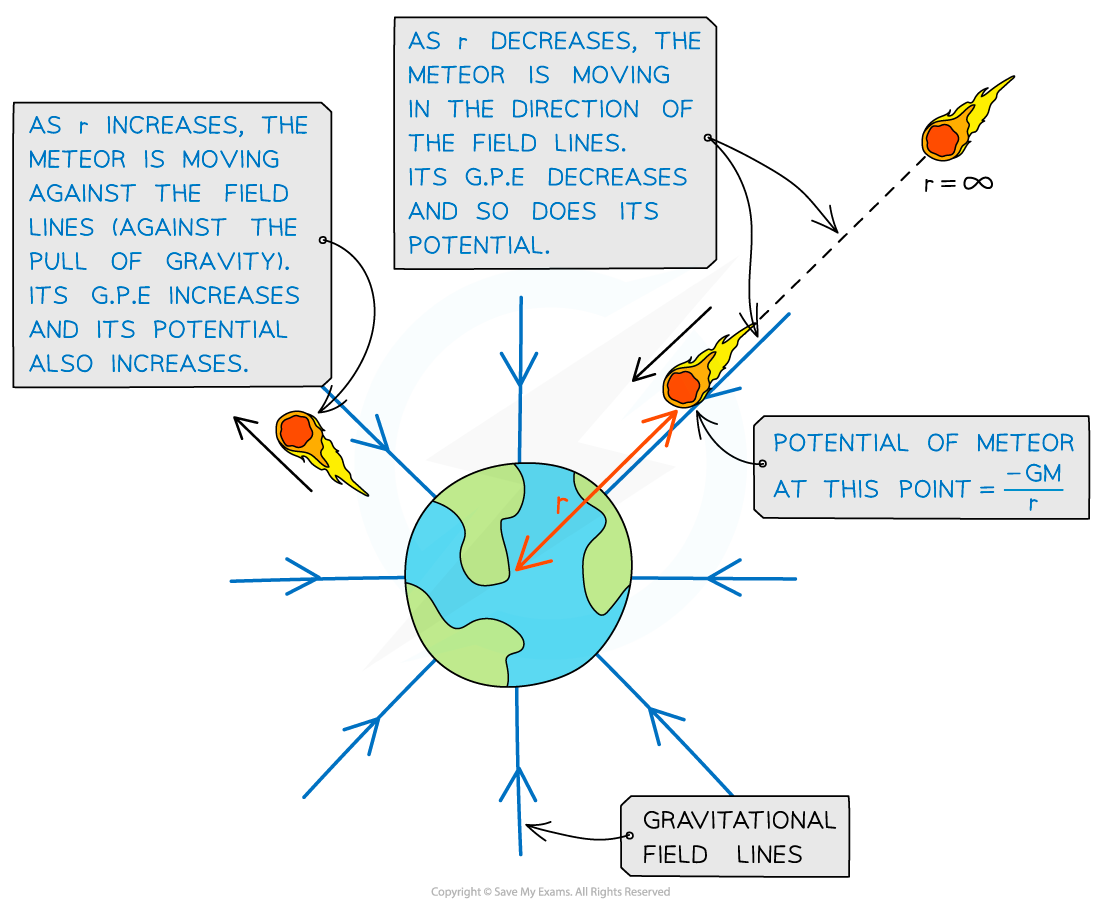
Gravitational potential increases and decreases depending on whether the object is travelling towards or against the field lines from infinity