Syllabus Edition

First teaching 2023

First exams 2025

Electric Potential Gradient (HL) (HL IB Physics)

Revision Note

Test yourself Flashcards

Author

Ann H

Last updated

7 August 2024

Work Done on a Charge

When a charge moves through an electric field, work is done
The work done in moving a charge q is given by:

$W = q ∆ V$

Where:
- W = work done on or by the field (J)
- q = magnitude of charge moving in the field (C)
- ΔV = potential difference between two points (J C⁻¹)

Electrical Potential Difference

Two points at different distances from a charge will have different electric potentials
- This is because the electric potential increases with distance from a negative charge and decreases with distance from a positive charge

Therefore, there will be an electric potential difference between the two points equal to:

$∆ V = V_{f} - V_{i}$

Where:
- V_f = final electric potential (J C⁻¹)
- V_i = initial electric potential (J C⁻¹)

The potential difference due to a point charge can be written:

$∆ V = k Q (\frac{1}{r_{f}} - \frac{1}{r_{i}})$

Where
- Q = magnitude of point charge producing the potential
- k = Coulomb constant (N m² C^–2)
- r_f = final distance from charge Q (m)
- r_i = initial distance from charge Q (m)

Worked example

A point charge of +7.0 nC is located 150 mm and 220 mm from points S and R respectively.

Work Done Electric Field Worked Example, downloadable AS & A Level Physics revision notes

Calculate the work done when a +3.0 nC charge moves from R to S.

Answer:

Step 1: Write down the known quantities

Final distance from charge, r_S = 150 mm = 0.15 m
Initial distance from charge, r_R = 220 mm = 0.22 m
Magnitude of charge producing the potential, Q = +7.0 nC = +7.0 × 10⁻⁹ C
Magnitude of charge moving in the potential, q = +3.0 nC = +3.0 × 10⁻⁹ C
Coulomb constant, k = 8.99 × 10⁹ N m² C⁻²

Step 2: Calculate the electric potential difference between R and S

$∆ V = k Q (\frac{1}{r_{S}} - \frac{1}{r_{R}})$

$∆ V = (8.99 \times 10^{9}) (7.0 \times 10^{- 9}) (\frac{1}{0.15} - \frac{1}{0.22}) = 133.5$ V

Step 3: Calculate the work done by the moving charge

$W = q ∆ V$

$W = (3.0 \times 10^{- 9}) \times 133.5 = 4.0 \times 10^{- 7}$ J

Examiner Tip

Remember that q in the work done equation is the charge that is being moved, whilst Q is the charge which is producing the potential.

Make sure not to get these two mixed up, as both could be given in the question (like the worked example) and you will be expected to choose the correct one.

Electric Potential Gradient

An electric field can be described in terms of the variation of electric potential at different points in the field
- This is known as the potential gradient

The potential gradient of an electric field is defined as:

The rate of change of electric potential with respect to displacement in the direction of the field

A graph of potential V against distance r can be drawn for a positive or negative charge Q
This is a graphical representation of the equation:

$V = \frac{k Q}{r}$

The gradient of the V-r graph at any particular point is equal to the electric field strength E at that point
This can be written mathematically as:

$E = - \frac{∆ V}{∆ r}$

Where:
- E = electric field strength (V m⁻¹)
- ΔV = potential difference between two points (V)
- Δr = displacement in the direction of the field (m)

The negative sign is included to indicate that the direction of the field strength E opposes the direction of increasing potential

Graph of electric potential against distance

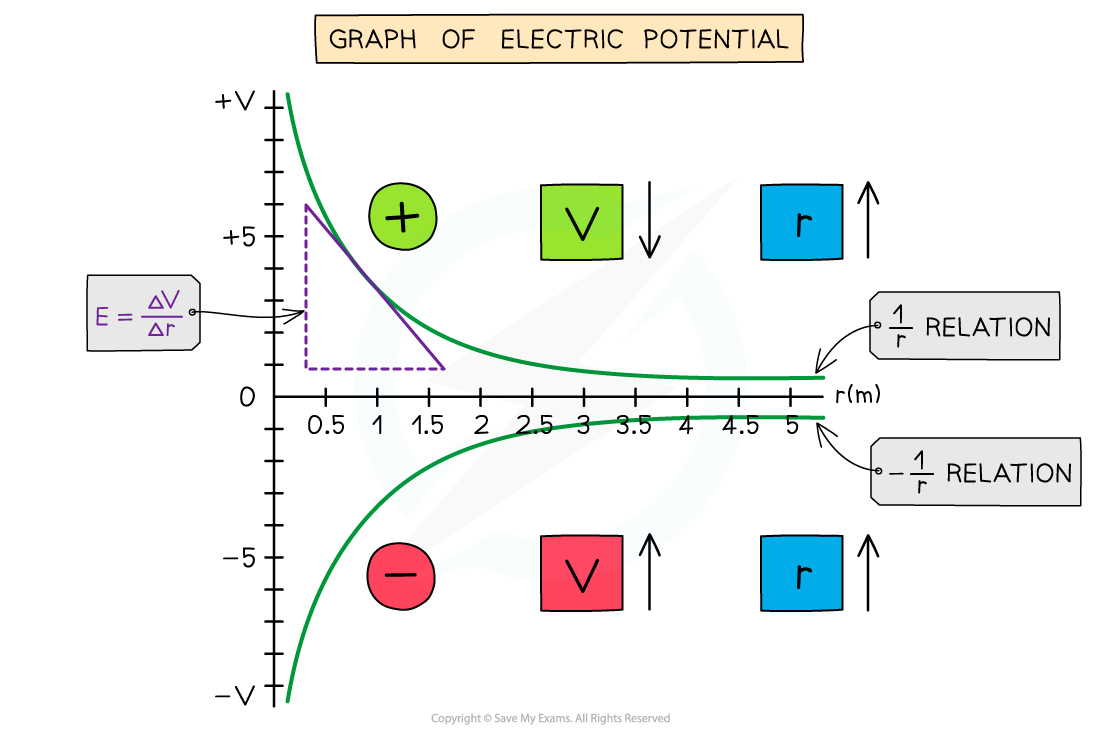
Electric Potential Gradient Graph

The electric potential around a positive charge decreases with distance and increases with distance around a negative charge

The key features of this graph are:
- All values of potential are negative for a negative charge
- All values of potential are positive for a positive charge
- As r increases, V against r follows a 1/r relation for a positive charge and a -1/r relation for a negative charge
- The gradient of the graph at any particular point is equal to the field strength E at that point
- The curve is shallower than the corresponding E-r graph

Determining potential from a field-distance graph

The potential difference due to a charge can also be determined from the area under a field-distance graph
A graph of field strength E against distance r can be drawn for a positive or negative charge Q
This is a graphical representation of the equation:

$E = \frac{k Q}{r^{2}}$

The area under the E-r graph between two points is equal to the potential difference ΔV between those points

Electric Field Strength and Distance Graph, downloadable AS & A Level Physics revision notes

The electric field strength E has a 1/r² relationship

The key features of this graph are:
- All values of field strength are negative for a negative charge
- All values of field strength are positive for a positive charge
- As r increases, E against r follows a 1/r² relation (inverse square law)
- The area under this graph is the change in electric potential ΔV
- The curve is steeper than the corresponding V-r graph

Examiner Tip

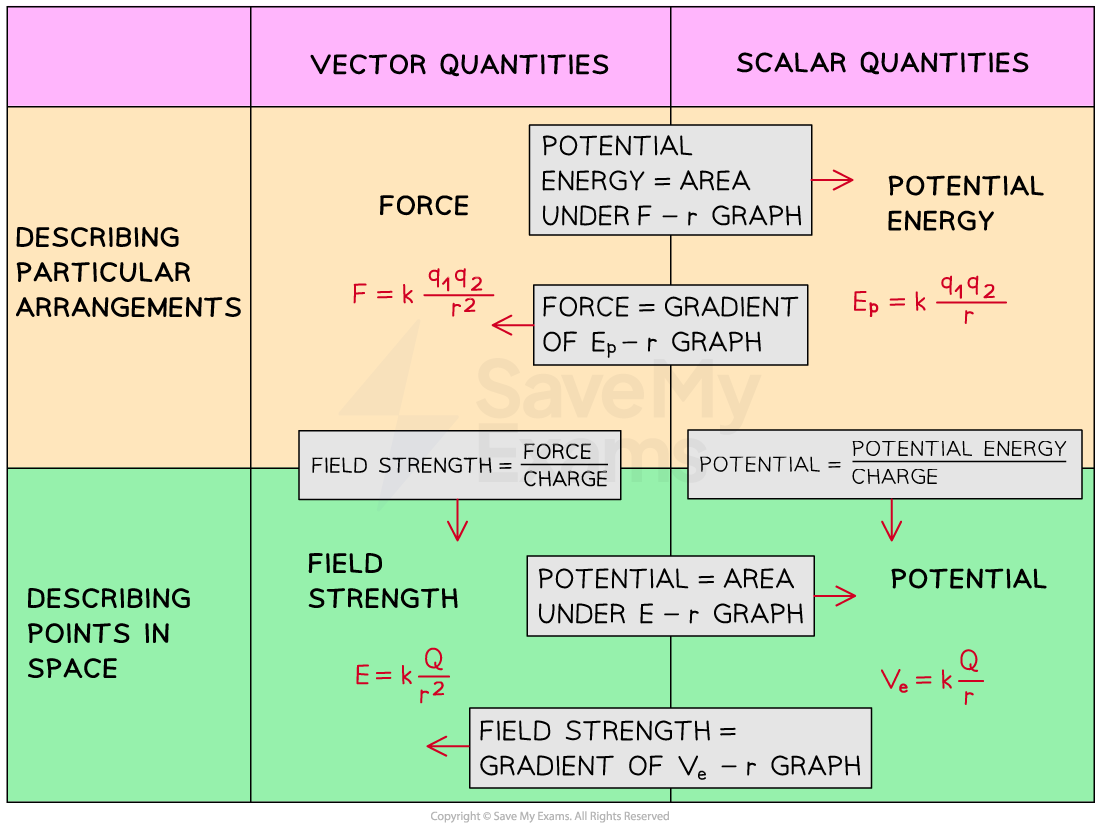
There are many equations and graphs to learn in this topic. A good way to revise these is to find a way of organising the knowledge in a way that resonates with you, here is an example of one possible way to do this: