Modelling with Trigonometric Functions (DP IB Analysis & Approaches (AA)) : Revision Note
Did this video help you?
Modelling with Trigonometric Functions
What can be modelled with trigonometric functions?
Anything that oscillates (fluctuates periodically) can be modelled using a trigonometric function
Normally some transformation of the sine or cosine function
Examples include:
is the depth of water at a shore t hours after midnight
is the temperature of a city d days after the 1st January
is vertical height above ground of a person t seconds after entering a Ferris wheel
Notice that the x-axis will not always contain an angle
In the examples above time or number of days would be on the x-axis
Depth of the water, temperature or vertical height would be on the y-axis
What are the parameters of trigonometric models?
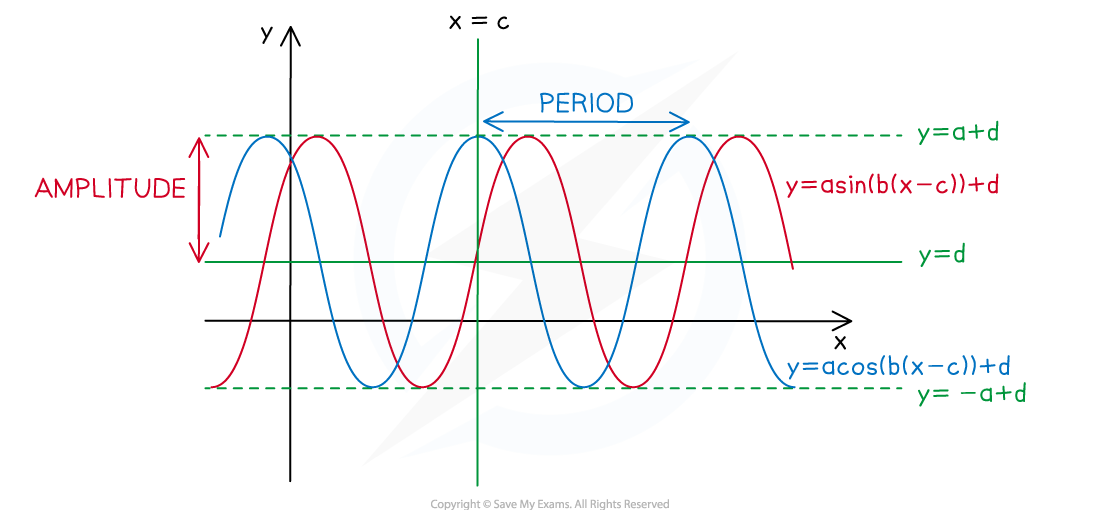
A trigonometric model could be of the form
The a represents the amplitude of the function
The bigger the value of a the bigger the range of values of the function
For the function
the amplitude is undefined
The b determines the period of the function
Period
The bigger the value of b the quicker the function repeats a cycle
The c represents the horizontal shift
The d represents the vertical shift
This is the principal axis
What are possible limitations of a trigonometric model?
The amplitude is the same for each cycle
In real-life this might not be the case
The function might get closer to the value of d over time
The period is the same for each cycle
In real-life this might not be the case
The time to complete a cycle might change over time
Examiner Tips and Tricks
The variable in these questions is often t for time.
Read the question carefully to make sure you know what you are being asked to solve.
Worked Example
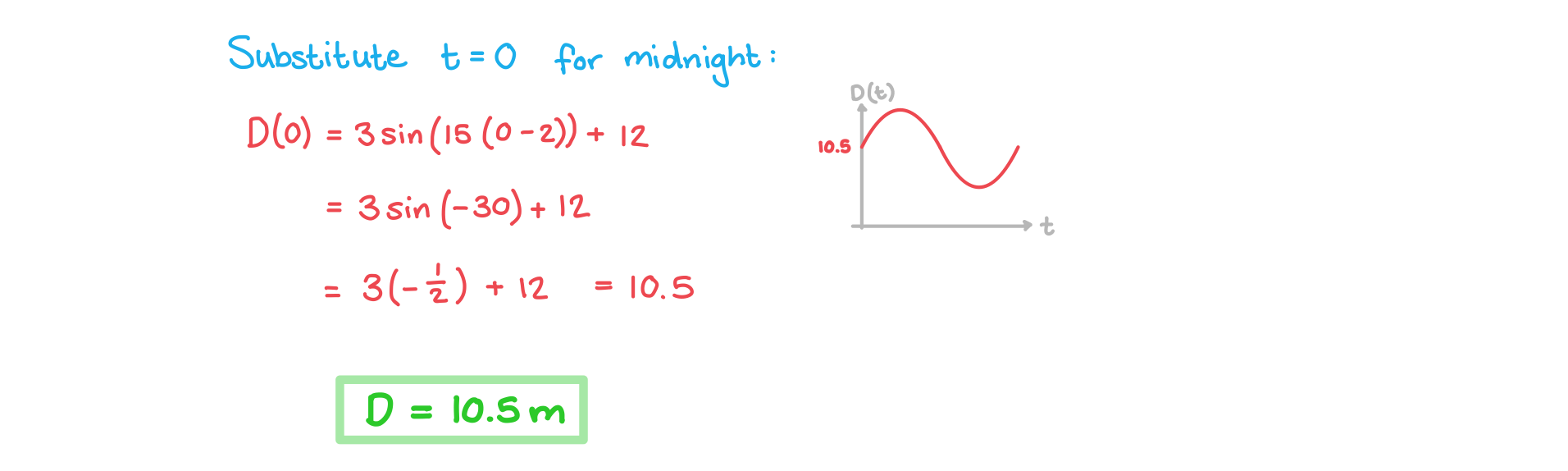
The water depth, D, in metres, at a port can be modelled by the function
where t is the elapsed time, in hours, since midnight.
a) Write down the depth of the water at midnight.
b) Find the minimum water depth and the number of hours after midnight that this depth occurs.

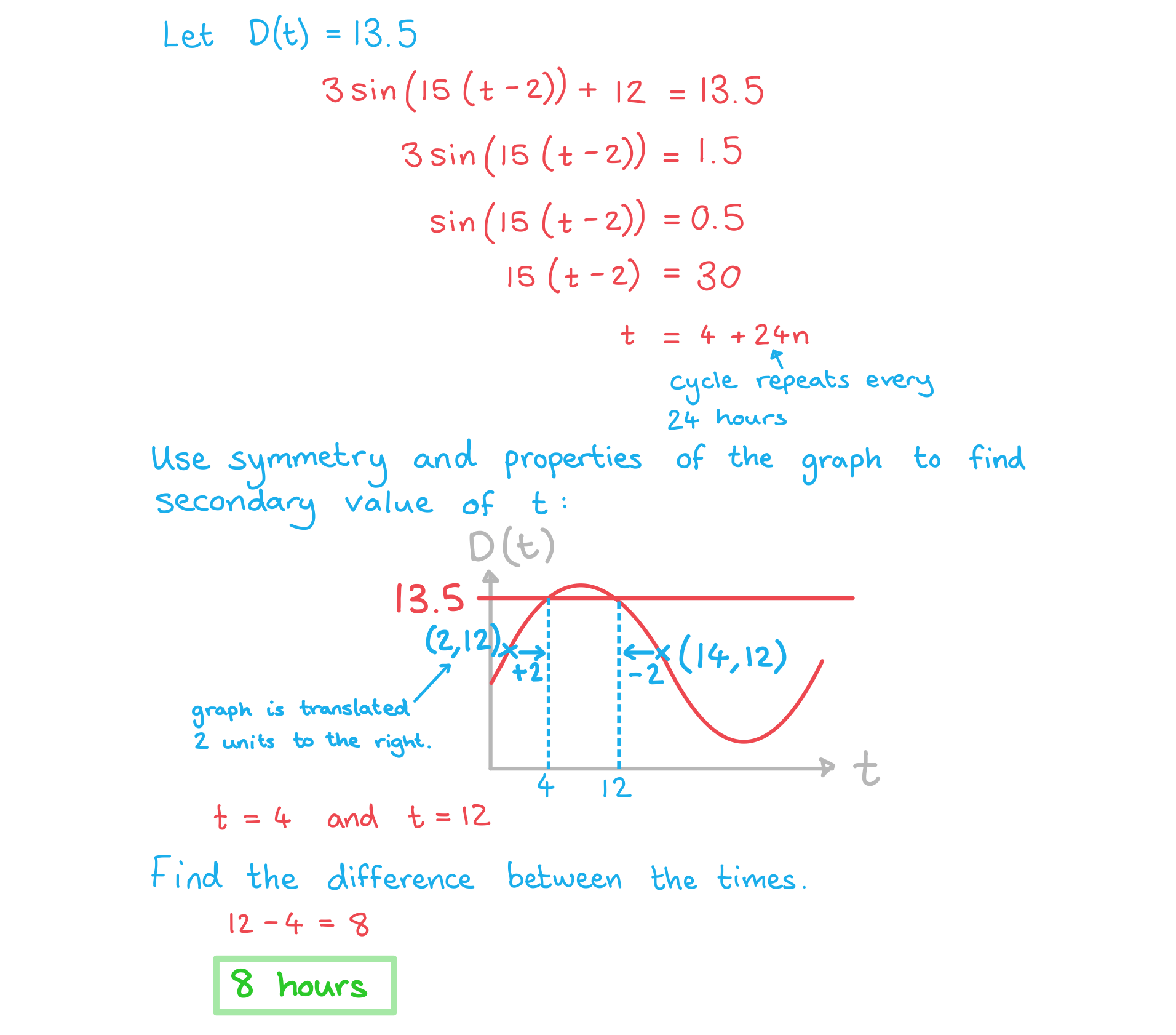
c) Calculate how long the water depth is at least 13.5 m each day.

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?
