Numerical Integration using the Trapezoid Rule (DP IB Applications & Interpretation (AI)) : Revision Note
Did this video help you?
Trapezoid Rule: Numerical Integration
What is the trapezoid rule?
The trapezoidal rule is a numerical method used to find the approximate area enclosed by a curve, the
-axis and two vertical lines
it is also known as ‘trapezoid rule’ and ‘trapezium rule’
The trapezoidal rule finds an approximation of the area by summing of the areas of trapezoids beneath the curve
etc
where
Note that there are
trapezoids (also called strips) but
function values
The trapezoidal rule is given in the formula booklet
What else can I be asked to do with the trapezoid rule?
Comparing the true answer with the answer from the trapezoid rule
This may involve finding the percentage error in the approximation
The true answer may be given in the question, found from a GDC or from work on integration
Examiner Tips and Tricks
Ensure you are clear about the difference between the number of data points (
values) and the number of strips (number of trapezoids) used in a Trapezoid Rule question
Although it shouldn't be too much trouble to type the trapezoid rule into your GDC in one go, it may be wise to work parts of it out separately and write these down as part of your working out
Worked Example
a) Using the trapezoidal rule, find an approximate value for
to 3 decimal places, using .
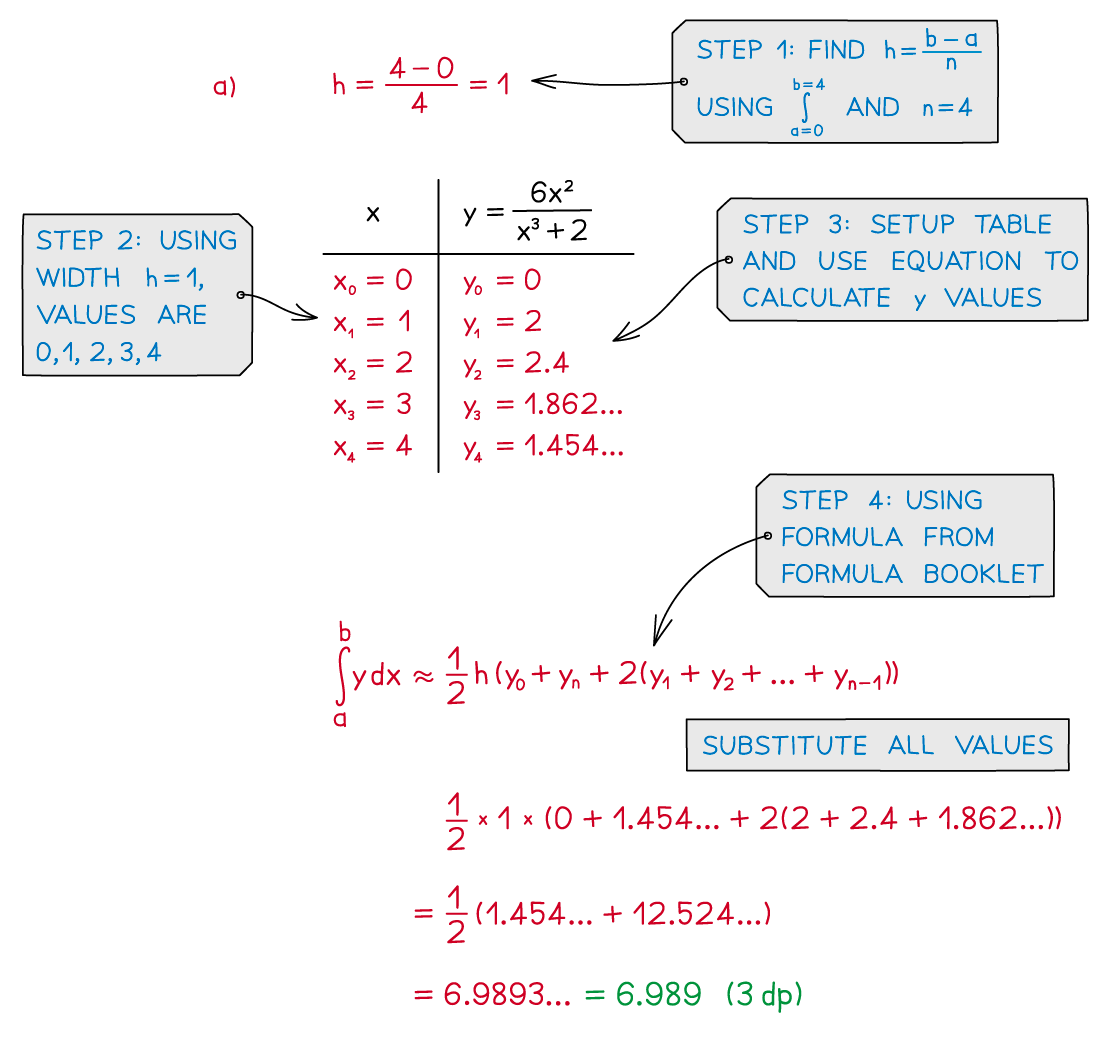
b) Given that the area bounded by the curve , the -axis and the lines
and
is 6.993 to three decimal places, calculate the percentage error in the trapezoidal rule approximation.


You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?
