Numerical Integration using the Trapezoidal Rule (DP IB Applications & Interpretation (AI)): Revision Note
Did this video help you?
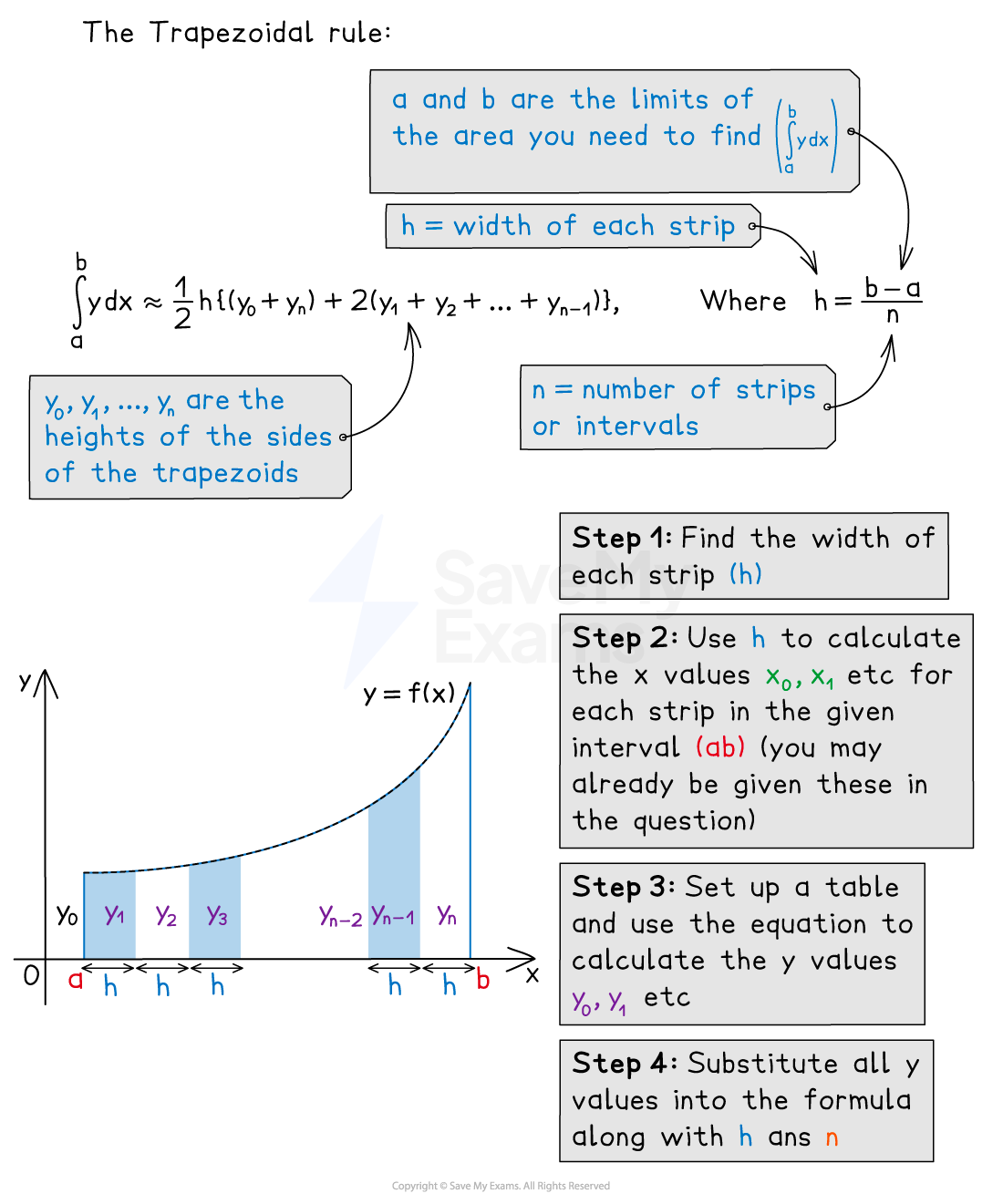
Trapezoid rule: numerical integration
What is the trapezoid rule?
The trapezoidal rule is a numerical method used to find the approximate area enclosed by a curve, the
-axis and two vertical lines
it is also known as ‘trapezoid rule’ and ‘trapezium rule’
The trapezoidal rule finds an approximation of the area by summing up the areas of trapezoids that lie (mostly) beneath the curve
For
, with
, etc., the approximation is given by
where
Note that there are
trapezoids (also called strips), but
function values
Examiner Tips and Tricks
The trapezoidal rule formula is given in the exam formula booklet.
What else can I be asked to do with the trapezoid rule?
Comparing the true answer with the answer from the trapezoid rule
This may involve finding the percentage error in the approximation
The true answer may be given in the question, found from a GDC or from work on integration
Examiner Tips and Tricks
Make sure you are clear about the difference between
the number of data points (
values)
and the number of strips (number of trapezoids)
used in a trapezoid rule question
Examiner Tips and Tricks
Although you can type the trapezoid rule into your GDC in one go, it may be wise to work out parts of it separately and write these down as part of your working out.
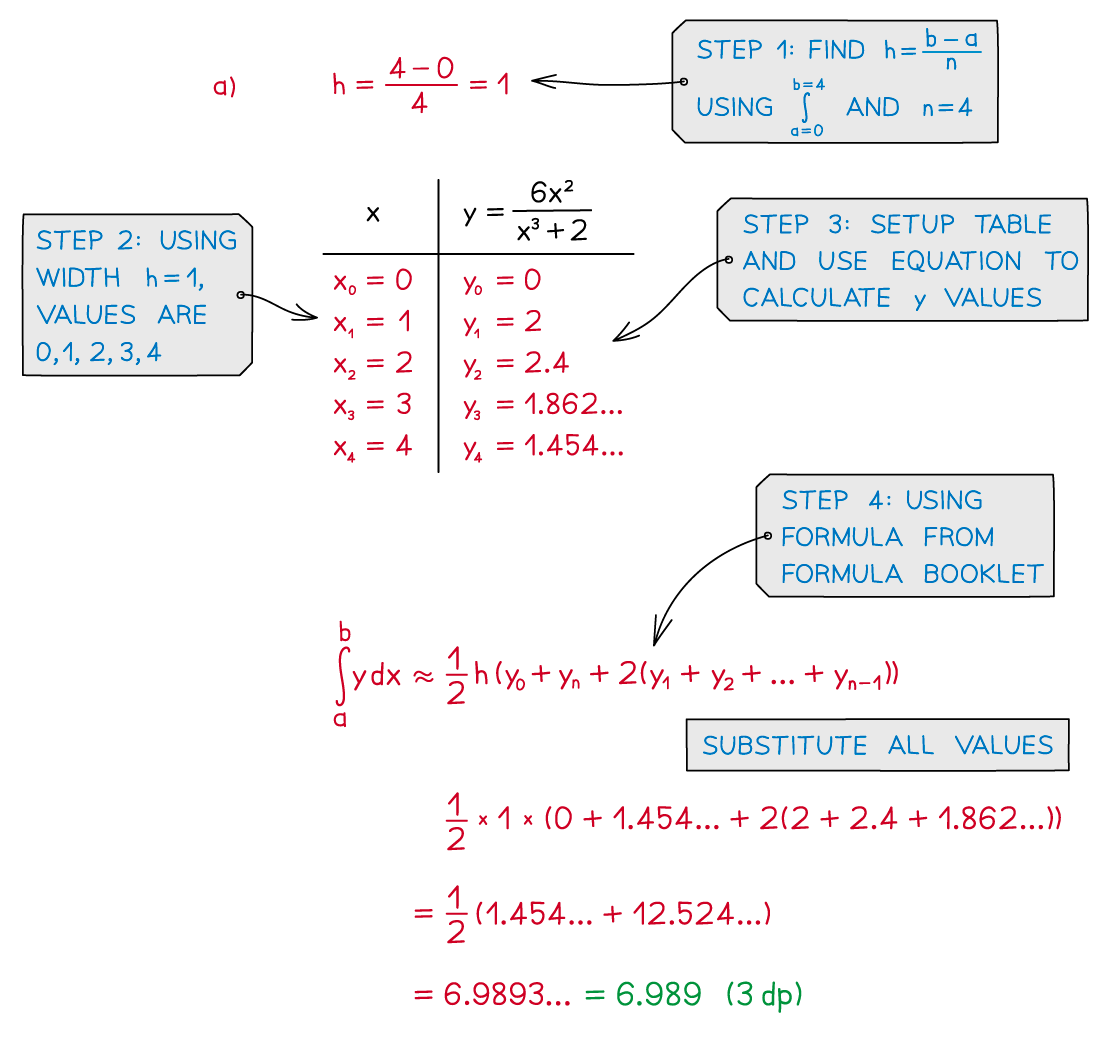
Worked Example
a) Using the trapezoidal rule, find an approximate value for
to 3 decimal places, using .
Answer:
b) Given that the area bounded by the curve , the -axis and the lines
and
is 6.993 to three decimal places, calculate the percentage error in the trapezoidal rule approximation.
Answer:


Unlock more, it's free!
Was this revision note helpful?