IBMaths: AI SLDPRevision Notes4. Statistics & Probability4.2 Correlation & Regression4.2.1 Bivariate data

Bivariate data (DP IB Maths: AI SL)

Revision Note

Test yourselfFlashcards
Dan

Author

Dan

Last updated

Did this video help you?

Scatter Diagrams

What does bivariate data mean?

  • Bivariate data is data which is collected on two variables and looks at how one of the factors affects the other
    • Each data value from one variable will be paired with a data value from the other variable
    • The two variables are often related, but do not have to be

What is a scatter diagram?

  • A scatter diagram is a way of graphing bivariate data
    • One variable will be on the x-axis and the other will be on the y-axis
    • The variable that can be controlled in the data collection is known as the independent or explanatory variable and is plotted on the x-axis
    • The variable that is measured or discovered in the data collection is known as the dependent or response variable and is plotted on the y-axis
  • Scatter diagrams can contain outliers that do not follow the trend of the data

Examiner Tip

  • If you use scatter diagrams in your Internal Assessment then be aware that finding outliers for bivariate data is different to finding outliers for univariate data
    • (x, y) could be an outlier for the bivariate data even if x and y are not outliers for their separate univariate data

Did this video help you?

Correlation

What is correlation?

  • Correlation is how the two variables change in relation to each other
    • Correlation could be the result of a causal relationship but this is not always the case
  • Linear correlation is when the changes are proportional to each other
  • Perfect linear correlation means that the bivariate data will all lie on a straight line on a scatter diagram
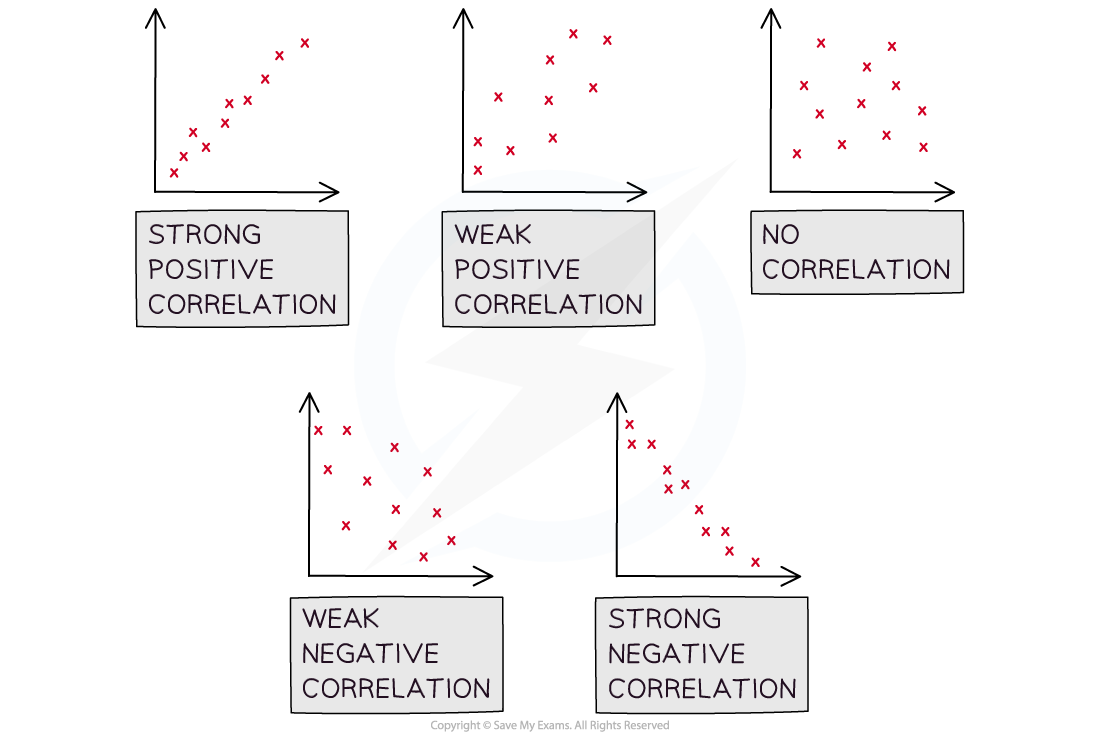
  • When describing correlation mention
    • The type of the correlation
      • Positive correlation is when an increase in one variable results in the other variable increasing
      • Negative correlation is when an increase in one variable results in the other variable decreasing
      • No linear correlation is when the data points don’t appear to follow a trend
    • The strength of the correlation
      • Strong linear correlation is when the data points lie close to a straight line
      • Weak linear correlation is when the data points are not close to a straight line
  • If there is strong linear correlation you can draw a line of best fit (by eye)
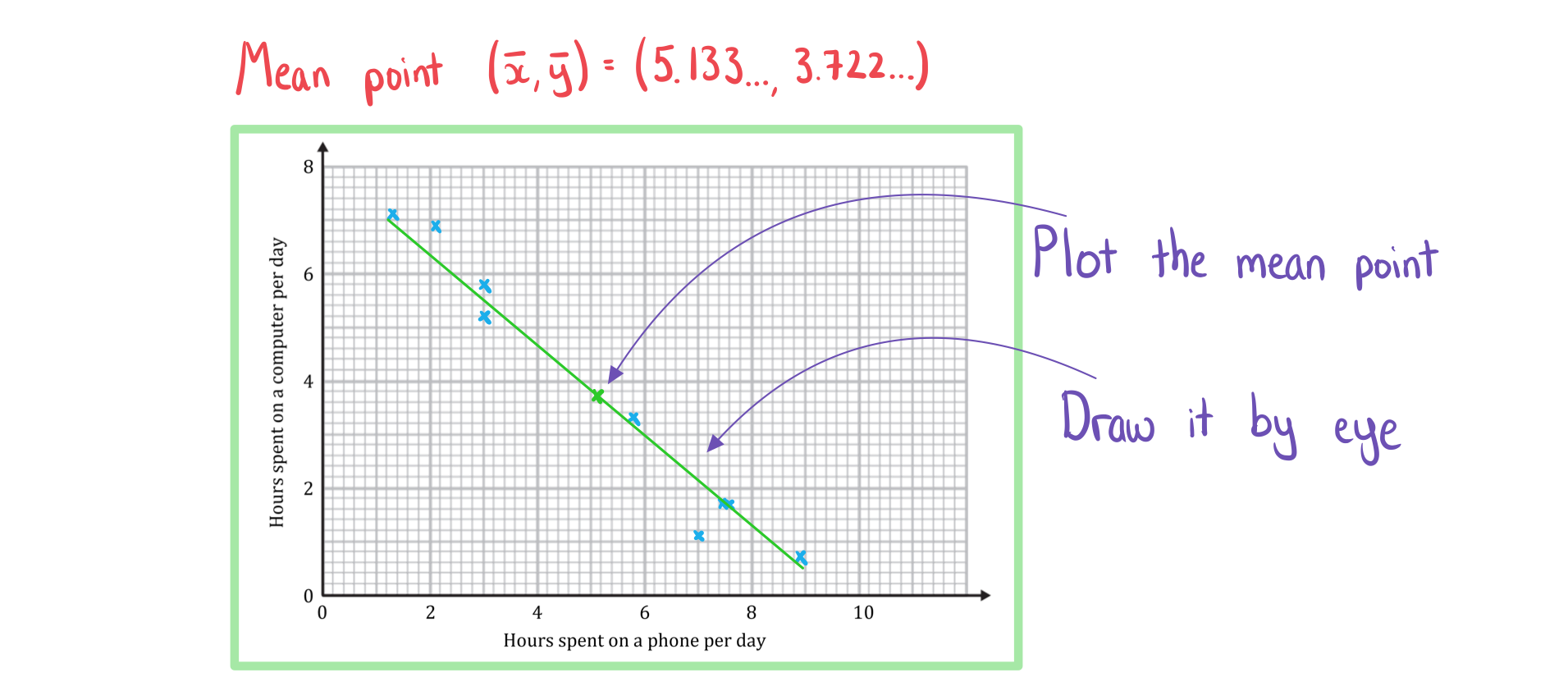
    • The line of best fit will pass through the mean point left parenthesis x with bar on top comma space y with bar on top right parenthesis
    • If you are asked to draw a line of best fit
      • Plot the mean point
      • Draw a line going through it that follows the trend of the data

2-4-1-correlation-diagram-1

What is the difference between correlation and causation?

  • It is important to be aware that just because correlation exists, it does not mean that the change in one of the variables is causing the change in the other variable
    • Correlation does not imply causation!
  • If a change in one variable causes a change in the other then the two variables are said to have a causal relationship
    • Observing correlation between two variables does not always mean that there is a causal relationship
      • There could be underlying factors which is causing the correlation
    • Look at the two variables in question and consider the context of the question to decide if there could be a causal relationship
      • If the two variables are temperature and number of ice creams sold at a park then it is likely to be a causal relationship
      • Correlation may exist between global temperatures and the number of monkeys kept as pets in the UK but they are unlikely to have a causal relationship

Worked example

A teacher is interested in the relationship between the number of hours her students spend on a phone per day and the number of hours they spend on a computer. She takes a sample of nine students and records the results in the table below.

Hours spent on a phone per day

7.6

7.0

8.9

3.0

3.0

7.5

2.1

1.3

5.8

Hours spent on a computer per day

1.7

1.1

0.7

5.8

5.2

1.7

6.9

7.1

3.3

a)
Draw a scatter diagram for the data.

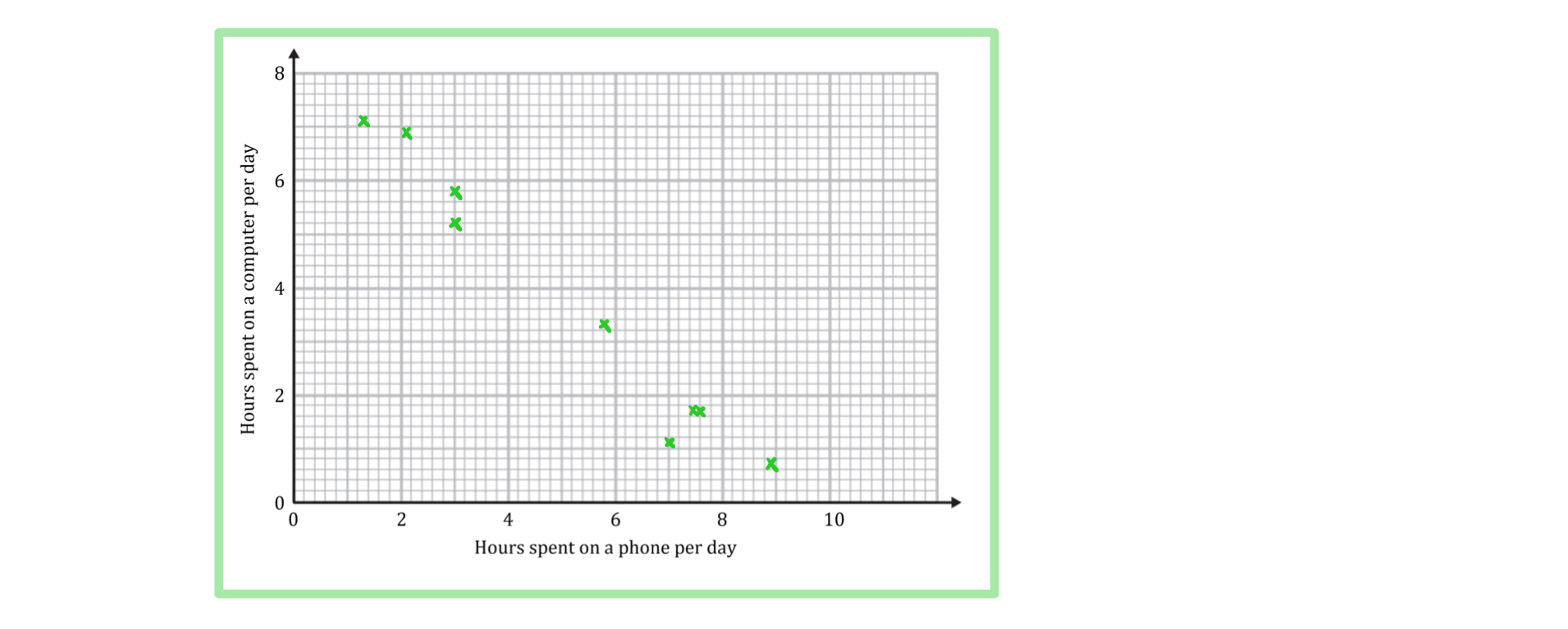
4-2-1-ib-ai-sl-correlation-a-we-solution

b)
Describe the correlation.

4-2-1-ib-ai-sl-correlation-b-we-solution

c)
Draw a line of best fit.

sPCr4WYi_4-2-1-ib-ai-sl-correlation-c-we-solution

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards

    Did this page help you?

    Previous:4.1.7 Interpreting DataNext:4.2.2 Correlation Coefficients
    Dan

    Author: Dan

    Expertise: Maths

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.