Coordinate Geometry (DP IB Maths: AI SL)

What are cartesian coordinates?

• Cartesian coordinates are basically the x-y coordinate system
  • They allow us to label where things are in a two-dimensional plane
• In the 2D cartesian system, the horizontal axis is labelled x and the vertical axis is labelled y

What can we do with coordinates?

• If we have two points with coordinates (x₁ , y₁) and (x₂ , y₂) then we should be able to find
  • The midpoint of the two points
  • The distance between the two points
  • The gradient of the line between them

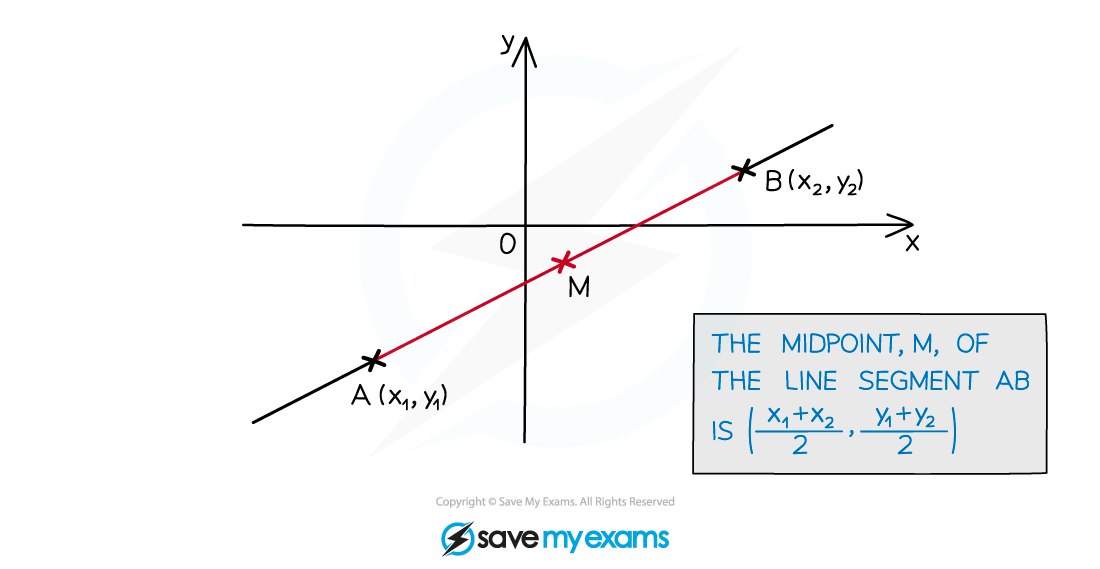
How do I find the midpoint of two points?

• The midpoint is the average (middle) point
  • It can be found by finding the middle of the x-coordinates and the middle of the y-coordinates
• The coordinates of the midpoint will be

• • This is given in the formula booklet under the prior learning section at the beginning

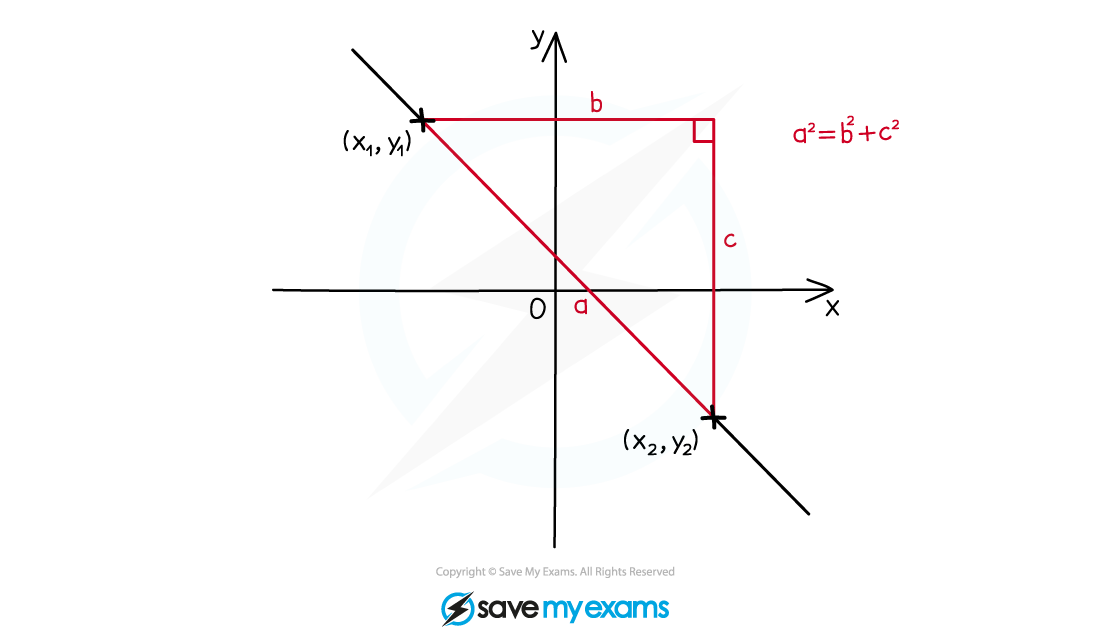
How do I find the distance between two points?

• The distance between two points with coordinates (x₁ , y₁) and (x₂ , y₂) can be found using the formula

• • This is given in the formula booklet in the prior learning section at the beginning

• Pythagoras’ Theorem  is used to find the length of a line between two coordinates
• If the coordinates are labelled A and B then the line segment between them is written with the notation [AB]

How do I find the gradient of the line between two points?

• The gradient of a line between two points with coordinates (x₁ , y₁) and (x₂ , y₂) can be found using the formula

• • This is given in the formula booklet under section 2.1 Gradient formula
  • This is usually known as  

What is a perpendicular bisector?

• A perpendicular bisector of a line segment cuts the line segment in half at a right angle
  • Perpendicular lines meet at right angles
  • Bisect means to cut in half
• Two lines are perpendicular if the product of their gradients is -1

How do I find the equation of the perpendicular bisector of a line segment?

• To find the equation of a straight line you need to find
  • The gradient of the line
  • A coordinate of a point on the line
• To find the equation of the perpendicular bisector of a line segment follow these steps:

• • STEP 1: Find the coordinates of the midpoint of the line segment
    • We know that the perpendicular bisector will cut the line segment in half so we can use the midpoint of the line segment as the known coordinate on the bisector
  • STEP 2: Find the gradient of the line segment

• • STEP 3: Find the gradient of the perpendicular bisector
    • This will be -1 divided by the gradient of the line segment
  • STEP 4: Substitute the gradient of the perpendicular bisector and the coordinates of the midpoint into an equation for a straight line
    • The point-gradient form is the easiest
  • STEP 5: Rearrange into the required form
    • Either   or   
    • These equations for a straight line are given in the formula booklet