Language of Sequences & Series (DP IB Applications & Interpretation (AI)) : Revision Note
Did this video help you?
Language of Sequences & Series
What is a sequence?
A sequence is an ordered set of numbers with a rule for finding all of the numbers in the sequence
For example 1, 3, 5, 7, 9, … is a sequence with the rule ‘start at one and add two to each number’
The numbers in a sequence are often called terms
The terms of a sequence are often referred to by letters with a subscript
In IB this will be the letter u
So in the sequence above, u1 = 1, u2 = 3, u3 = 5 and so on
Each term in a sequence can be found by substituting the term number into formula for the nth term
What is a series?
You get a series by summing up the terms in a sequence
E.g. For the sequence 1, 3, 5, 7, … the associated series is 1 + 3 + 5 + 7 + …
We use the notation Sn to refer to the sum of the first n terms in the series
Sn = u1 + u2 + u3 + … + un
So for the series above S5 = 1 + 3 + 5 + 7 + 9 = 25
Worked Example
Determine the first five terms and the value of S5 in the sequence with terms defined by un = 5 - 2n.

Did this video help you?
Sigma Notation
What is sigma notation?
Sigma notation is used to show the sum of a certain number of terms in a sequence
The symbol Σ is the capital Greek letter sigma
Σ stands for ‘sum’
The expression to the right of the Σ tells you what is being summed, and the limits above and below tell you which terms you are summing

Be careful, the limits don’t have to start with 1
For example
or
r and k are commonly used variables within sigma notation
Examiner Tips and Tricks
Your GDC will be able to use sigma notation, familiarise yourself with it and practice using it to check your work
Worked Example
A sequence can be defined by for
.
a) Write an expression for using sigma notation.
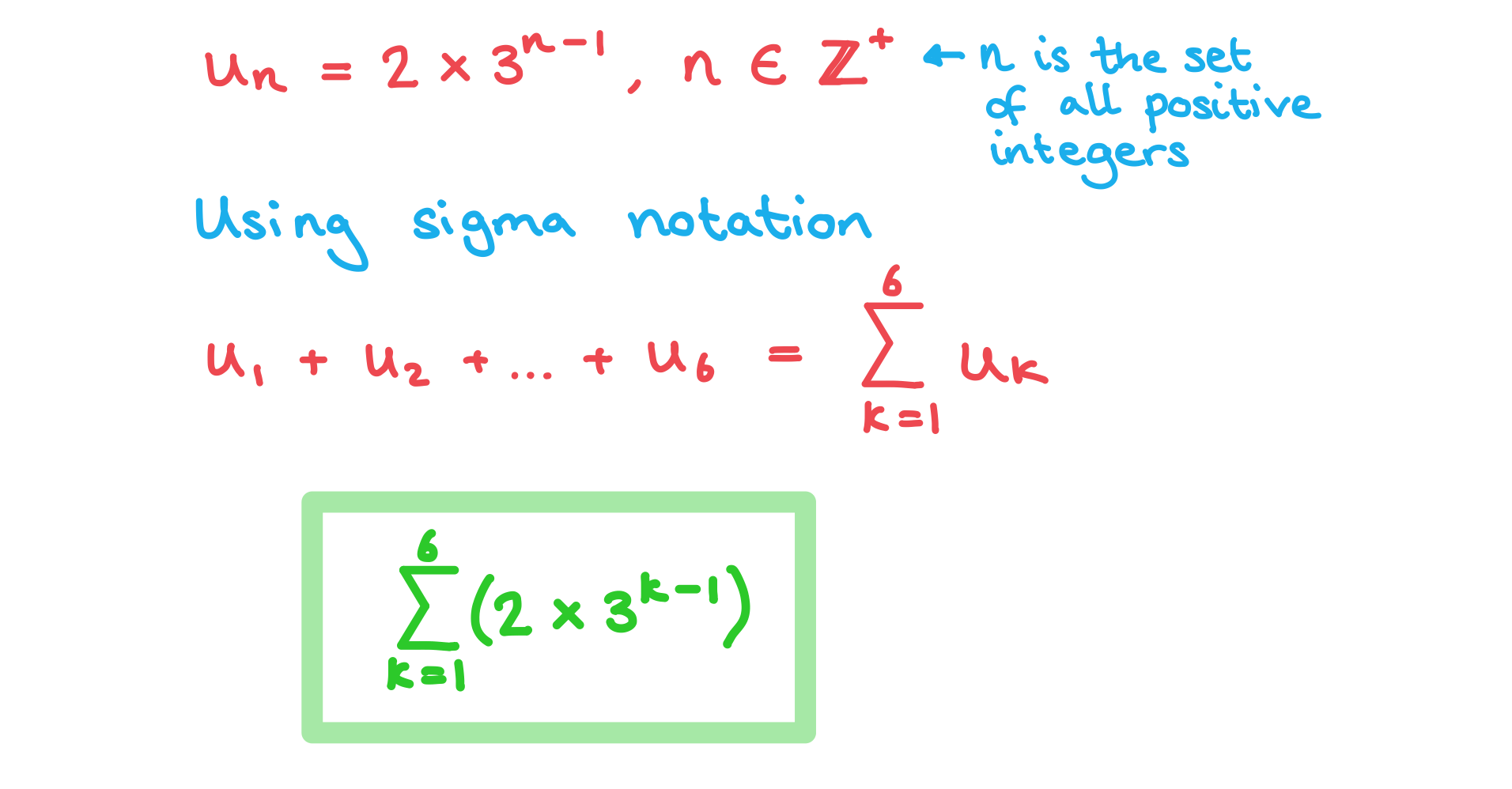
b) Write an expression for using sigma notation.
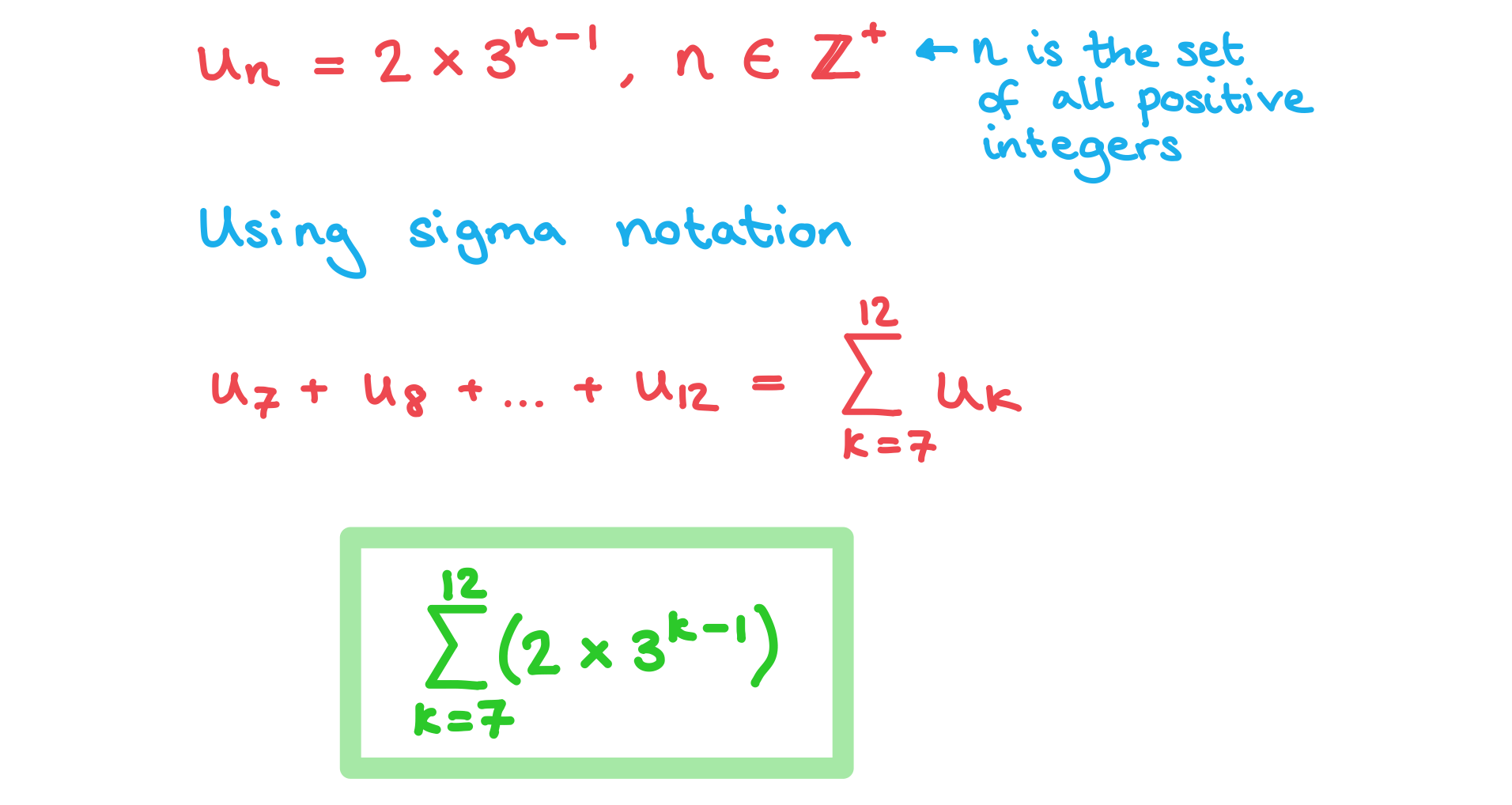

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?
