Find the indefinite integral for
Show that the exact value of the definite integral
is .
Find the indefinite integral for
Did this page help you?
Select a download format for 5.4 Further Integration
Find the indefinite integral for
How did you do?
Show that the exact value of the definite integral
is .
How did you do?
Find the indefinite integral for
How did you do?
Did this page help you?
Integrate
How did you do?
Show that
where is a constant of integration.
How did you do?
Find an expression for given that
and that when
.
How did you do?
Did this page help you?
Find the indefinite integral for
How did you do?
Find the indefinite integral for
How did you do?
Did this page help you?
Given that , find
.
How did you do?
Hence, or otherwise, find
How did you do?
Did this page help you?
Consider the function .
Find
How did you do?
Hence, find
How did you do?
Did this page help you?
Let
Find given that
.
How did you do?
Did this page help you?
Show that
How did you do?
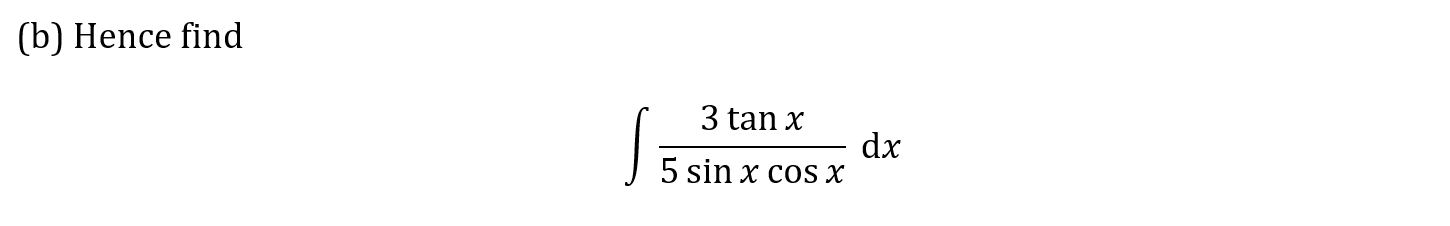
How did you do?
Did this page help you?
The diagram below shows the graphs of the line and the curve

Point is the point of intersection of the curve
with the
-axis. Point
is the point of intersection of the curve
with the line
for which
. Point
is the point of intersection of the line
with the
-axis.
Write down the -coordinates of points
How did you do?
Calculate the area of the shaded region.
How did you do?
Did this page help you?
The diagram below shows the graph of the function which is defined by

The shaded region in the diagram is the region enclosed by the -axis and the graph of
.
Find the area of the part of the shaded region that lies above the -axis.
How did you do?
Find the area of the entire shaded region.
How did you do?
Did this page help you?
The diagram below depicts the design for a new company logo. The logo is formed by a circle centred on the origin, which is divided into two regions by the curve where
is the function defined by
. The points where the circle and the curve intersect lie on the
-axis, as shown.

The shaded region in the diagram is the region inside that circle that lies below the curve .
How did you do?
Find the percentage of the circular logo that is shaded.
How did you do?
Did this page help you?
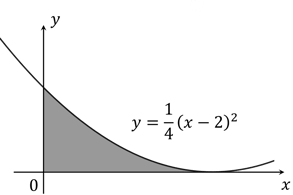
The following diagram shows a part of the graph of the curve . The shaded region is the region enclosed by the graph and the positive
- and
-axes.
How did you do?
Find the area of the shaded region
How did you do?
Find the volume of the solid formed when the shaded region is rotated radians about the
-axis.
How did you do?
Find the volume of the solid formed when the shaded region is rotated radians about the
-axis.
How did you do?
Did this page help you?
The diagram below shows the cross-section of a bowl that a company is planning to begin producing.
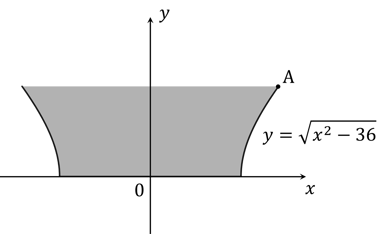
As indicated on the diagram, one of the sides of the bowl in the cross-section may be described by the curve , where units for
and
are centimetres. The cross-section is entirely symmetrical about the
-axis. The flat circular bottom of the bowl has a diameter of 12 cm, and the vertical depth of the bowl is 6 cm. For purposes of answering this question, the thickness of the bottom and sides of the bowl may be regarded as negligible.
Find the exact coordinates of the point marked on the diagram.
How did you do?
Show that the capacity of the bowl in cm3 is given by
where is a constant to be determined.
How did you do?
Hence find the capacity of the bowl.
How did you do?
Did this page help you?
Consider the function defined by
Find the coordinates of the points where the graph of intercepts the
-axis.
How did you do?
Find the indefinite integral
How did you do?
Use your answer to part (b) to calculate the area of the region enclosed by the graph of and the
-axis.
How did you do?
Did this page help you?
Find the indefinite integral for
How did you do?
Find the indefinite integral for
How did you do?
Find an expression for given that
How did you do?
Did this page help you?
Find the indefinite integral
How did you do?
Find an expression for given that
and also that when
.
How did you do?
Did this page help you?
Find the indefinite integral for
How did you do?
Find the indefinite integral for
How did you do?
Did this page help you?
Consider the function .
How did you do?
Let
Find given that
.
How did you do?
Did this page help you?
Work out the following indefinite integrals:
How did you do?
How did you do?
Did this page help you?
Use definite integration to find the exact value of
giving your final answer in as simple a form as possible.
How did you do?
Did this page help you?
The diagram below shows the graph of the function which is defined by

The shaded region in the diagram is the region enclosed by the -axis and the graph of
.
Explain why the area of the shaded region is not equal to
How did you do?
Find the area of the entire shaded region.
How did you do?
Find the individual areas of the parts of the shaded region (i) above and (ii) below the x-axis.
How did you do?
Did this page help you?
The shaded region in the diagram below depicts the design for a new company logo. The upper border of the logo is formed by a part of the curve with equation , while the lower border of the logo is formed by a part of the curve with equation
. The points where the two curves intersect lie on the
-axis, as shown.

Find the exact coordinates of
How did you do?
Hence find the area of the company logo.
How did you do?
Did this page help you?
The following diagram shows a part of the graph of the curve , where
is a constant. The point marked A is the vertex of the curve. Region
is the region enclosed by the curve and the
-axis. Region
is the region enclosed by the curve, the positive
-axis, and the line through point A with gradient zero.

Show that the part of the curve bordering the region can also be represented by the curve with equation .
How did you do?
When region is rotated
radians about the
-axis, the resultant solid of revolution has a volume equal to
.
Find the value of .
How did you do?
Use the result from part (a) to find the area of region .
How did you do?
Use your answer to part (c) to write down the area of region R.
How did you do?
Did this page help you?
The diagram below shows the cross-section of a miniature goldfish bowl produced by Some Things Fishy, a specialist company supplying products for miniature goldfish enthusiasts.

The glass part of the bowl sits on a solid base, indicated by the shaded region on the diagram. The cross-section of the glass part of the bowl is symmetrical about the -axis, and may be described by the curve with equation
The dashed horizontal line represents the diameter of the open top of the fishbowl. All coordinates are expressed in centimetres, and for purposes of answering this question the thickness of the glass sides of the bowl may be regarded as negligible.
Given that the diameter of the open top of the fishbowl is 15 cm, and that this is less than the diameter of the fishbowl at its widest point, find the capacity of the glass part of the fishbowl.
How did you do?
Did this page help you?
Consider the function defined by
Find the indefinite integral
How did you do?
Use your answer to part (a) to calculate the area of the region enclosed by the graph of and the
-axis.
How did you do?
Did this page help you?
Find the indefinite integral for
How did you do?
Find the indefinite integral for
How did you do?
Find an expression for given that
How did you do?
Did this page help you?
Find the indefinite integral
How did you do?
Find an expression for given that
and also that when
How did you do?
Did this page help you?
Find the indefinite integral for
How did you do?
Find the indefinite integral for
How did you do?
Did this page help you?
Find the indefinite integral
How did you do?
Let for
Find given that
.
How did you do?
Show that
How did you do?
Did this page help you?
A curve with equation is such that
where is a real constant.
Given that the curve passes through the points and
, find
.
How did you do?
Did this page help you?
Explain why
How did you do?
Use definite integration, along with the result from part (a), to show that
How did you do?
Using your knowledge of the natural logarithm function, explain (without using your GDC) why the value of the integral found in part (b) is a positive number.
How did you do?
Did this page help you?
The diagram below shows the graph of the function which is defined by

The shaded region in the diagram is the region enclosed by the -axis and the graph of
. The three sub-parts of the shaded region are denoted by R, S and T, as shown.
Find the value of
How did you do?
Find the individual areas of each of the three sub-parts R, S and T of the shaded region.
How did you do?
Compare the sum of the answers in part (b) to the answer in part (a) and comment on the result.
How did you do?
Did this page help you?
The diagram below depicts the design for a new company logo. The upper border of the logo is formed by a part of the curve with equation , while the lower border of the logo is formed by a part of the curve with equation
. As shown in the diagram, the logo is divided into a shaded part and an unshaded part by a part of the curve with equation
.

Find the percentage of the total area of the logo that is shaded.
How did you do?
Did this page help you?
The following diagram shows a part of the graph of the curve with equation , where
is a constant. The point marked A is the vertex of the curve. Region
is the region enclosed by the curve and the
-axis, for the part of the curve where
is non-negative. Region
is the region enclosed by the curve, the positive
-axis, and the line through point A with gradient zero.

When region is rotated
radians about the
-axis, the resultant solid of revolution has a volume equal to
.
Find the area of region by calculating an area between the curve and the
-axis.
How did you do?
Find the area of region S by calculating an area between the curve and the -axis. Confirm that this matches your answer to part (a).
How did you do?
Did this page help you?
The diagram below shows the cross-section of a goldfish bowl to be produced by Pieseize Manufacturing, a specialist company supplying products for goldfish enthusiasts.

The glass part of the bowl sits on a solid base, indicated by the shaded region on the diagram. The cross-section of the glass part of the bowl is symmetrical about the -axis, and may be described by the curve with equation
The dashed horizontal line represents the diameter of the open top of the fishbowl. The maximum depth of the fishbowl, measured along the -axis from the diameter of the open top to where the glass part of the bowl meets the base, is indicated by
in the diagram. All coordinates are expressed in centimetres, and for purposes of answering this question the thickness of the glass sides of the bowl may be regarded as negligible.
The owner of the company, Skodyn Pieseize, is extremely superstitious and is obsessed with the number 23. Therefore he insists that the capacity of the glass part of this new fishbowl must be exactly 23 litres. Find the value of that satisfies this requirement.
How did you do?
Did this page help you?