120 students went on a school trip to the Thormton Manor theme park. A statistics student has begun filling in the following Venn diagram, showing the numbers of students who went on none, one or more of the park’s three most terrifying rides: the Aquaplunge water slide (A) , the Barnstormer rollercoaster (B), and the Really Scary Carousel (C).
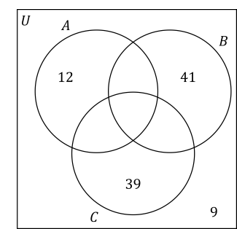
A student is randomly chosen from the group that went to the theme park.
Given that ‘went on Aquaplunge’ and ‘went on the Really Scary Carousel’ were mutually exclusive events, while ‘went on Aquaplunge’ and ‘went on the Barnstormer’ were independent events, find the probability that the student:
(i)
went on the Really Scary Carousel
(ii)
did not go on exactly two of the rides
(iii)
went on Aquaplunge, given that they went on the Barnstormer
(iv)
went on the Barnstormer, given that they went on less than two of the rides
(v)
went on the Really Scary Carousel, given that they did not go on Aaplunge.





