Geometry of 3D Shapes (DP IB Maths: AI HL)

A trapezoidal prism, ABCDEFGH, is shown in the diagram below. The length of the base is 7.5 cm and the width is 6.3 cm.  The height of the prism is 6.5 cm and the length BF is 8.8 cm.  In the trapezoidal cross-section ABFE side AB is parallel to side EF.

Calculate the length AB.

Find the size of the angle .

In the diagram below ABCD is the square base of a right pyramid with vertex V. The centre of the base is M. The sides of the square base are 4.2 cm and the vertical height is 10.6 cm.

Calculate the area of the triangle .

Calculate the length of .

Find the size of the angle makes with the square base

A symmetrical candle with the shape of a right circular cone has a circular base with radius cm and an initial height of  cm. As the candle burns the height decreases, and the shapes of the candle becomes a frustum with the same base radius.

Find an expression, in terms of , for the height of the remaining unburnt candle, , when exactly a quarter of the initial volume has been burnt.

The height of the candle is 5cm when a quarter of its volume has been burnt.

Calculate the initial height of the candle.

ABCDEF is a pencil case in the shape of a triangular prism. The end of the pencil case is an isosceles triangle where AC = 4 cm and AB = BC = 6 cm. The length of the pencil case is 11 cm. M is the midpoint of AC. This information is shown in the diagram below.

Show that the volume of the pencil case is .

Calculate angle .

Find the length of the longest pencil that could fit into the pencil case.

A coffee scoop is made out of 2 mm thick stainless steel. It is in the shape of a hemisphere and has an outer diameter of 3.8 cm.

Show that the outer surface area of the scoop is  

Calculate the volume of coffee that the scoop can hold, in .

The density of the coffee when compacted in the scoop is 0.825 g/cm³.  A single bag of ground coffee beans contains 350 g and costs $16. 

Calculate the cost per scoop of ground coffee.

Two points, A (2, 1, 3) and B (5, 2, 6), are located on an xyz coordinate grid as shown in the diagram below.

Find the length of AB.

Find the coordinates of the midpoint of [AB].

Calculate the angle between the line (AB) and xy plane.

A number of model buildings are created in the shape of a rectangular based right pyramid. A single model, ABCDE, has a base of 4.6 cm by 7.2 cm and a slant height of 8.3 cm, as shown in the diagram below.

Calculate the volume of one of the models.

The entire surface of the model is to be painted with the exception of the base, which will be glued to the surface on which the models are to be set up.  An 18 ml pot of model paint will cover an area of 120 .

Calculate the number of pots of paint that would need to be purchased to paint 8 of these models.

The packaging for a particular firework consists of a thin piece of cardboard in the shape of a right cone with a height of 7.5 cm. The radius of the base is 5.3 cm.

Calculate the area of cardboard required for the packaging.

Calculate the volume of the cone.

The firework company wants to reduce the amount of packaging material used without changing the volume of the cone.  

Calculate the radius that the cone needs to be if the height is increased to 7.8 cm. Give your answer to 1 decimal place.

Using your answer from part (c) show that the new cone will require less packaging material than the original cone.

A company manufactures metal doorknobs that consist of a cylinder of radius 27 mm and height 20 mm topped with a solid hemisphere. The cylindrical portion is also solid, save for a cylindrical hole in the base with diameter 4 mm and depth 19 mm to accommodate a screw. The axis of the cylindrical hole is perpendicular to the base of the doorknob. A diagram showing this information can be seen below.

Show that the volume of material required to construct the doorknob is .

The cost of the metal used to make the doorknob has risen to .

Calculate the amount of money that will be saved per doorknob if the diameter of the doorknob is reduced by 5 mm. Give your answer to 2 decimal places.

A rectangular swimming pool is to be constructed with length 22 m and width 14 m. The depth of the swimming pool is 3.1 m at the deep end rising to 1.2 m at the shallow end as shown in the diagram below. The four vertical sides of the swimming pool are all perpendicular to the horizontal top surface.

The pool is filled to a height of 14 cm below the top edge of the pool.

Calculate the volume of water in the swimming pool.

A partial draining of the water is required to investigate a problem with one of the walls, so  of the water is temporarily removed. 

Find the height of the water that is now in the deepest part of the pool.

Calculate the area of the base of the pool that is left uncovered by water.

Sphere 1 has radius , volume  and surface area , and sphere 2 has radius , volume  and surface area . Sphere 2 has eight times the mass of sphere 1 and both spheres are made out of the same material.  Find the ratio of extra paint needed to paint the surface of sphere 2 compared to that needed to paint the surface of sphere 1.

A lunchbox has a rectangular base of length 18 cm and width 12.5 cm. The height of the box at the front, shallower end is 6.4 cm, rising to a height of 9.6 cm at the far end. There is an internal divider that is parallel to the front and the back, situated at a distance of  cm from the shallower end of the box. All of the sides are perpendicular to the base.  
A diagram representing this information is given below.

Calculate the total volume of the lunchbox.

Show that the volume of the front, shallower compartment can be expressed as

A firepit is constructed from a solid cuboid of stone, ABCDEFGH, with a length and width of 62 cm and a height of 42 cm. A depression in the shape of a hemisphere with diameter 48 cm is removed from the centre of the top face of the cuboid. M is the centre of the base of the hole. This information can be seen in the diagram below.

Calculate the distance MA.

The density of the stone is .

Calculate the mass of a single firepit.

The cost of the stone is AUS  and labour costs AUS  per hour.  It takes 4 hours to make one firepit. The company constructing the firepits has a budget of AUS .  

Calculate the number of firepits that can be constructed within budget. You need only consider the volume of stone in a completed firepit in your answer.

A building is to be constructed with a concrete slab foundation. In order to accommodate this foundation, a rectangular section of earth measuring 25 m by 28 m is removed to a depth of 1.3 m. The removed earth is used to create a hemispherical landscaped feature in order to reduce waste.  

Calculate the diameter of the landscaped hemisphere that can be created.

The architect has decided that a cylindrical area 2 m in height would be more appropriate than a hemisphere as a design feature.

Given that the maximum straight-line distance that is available on the site for landscaping features is 20 m, show that the cylindrical design would not be suitable for the site.

The diagram below shows a product in the shape of a sphere with radius 3.6 cm. The product is packed in cuboidal packing crates measuring 1.7 m by 0.9 m with a depth of 22 cm. The spheres are stacked directly on top of and next to each other, using gum to fix them in position. Each layer contains the same number of spheres.

Find the number of spheres that can be packed in a single crate.

Calculate the volume of unused space between the spheres.

The company that has created the product wants to reduce costs by increasing the number of items that they can pack in one crate. They re-design the product in the shape of a cylinder keeping the radius and the volume the same.

Show that, to 3 significant figures, there is a 30.9% decrease in unused space in the packing crate if the cylindrical tube design is used instead of the spherical design.

The diagram below shows a door wedge, .   is a horizontal surface and angles and  are right angles. The face is a square face parallel to  with the centres ofand  being aligned.  ,  ,    and  . This information is represented in the diagram below.

Find the size of the angle .

Calculate the length AG.

The diagram below shows a frustum, , that has been made by removing a square based pyramid of height  from a solid square based pyramid of height and base length . Plane is parallel to plane .

Calculate the volume of the frustum.

Calculate the surface area of the frustum.

Find the length AG.

A cuboid, ABCDEFGH, has sides of length , and .  

A diagram representing this information is shown below.

Show that the length BH can be expressed as 

Find an expression that describes the surface area of the cuboid.

M is the midpoint of AF.

Find the angle that the line MG makes with the horizontal plane.

An ice cream cone is in the form of a right cone with a slant height of 9.1 cm and a perpendicular height of 8.7 cm. The bottom of the ice cream cone is filled with chocolate. The top of the chocolate layer is a circle of diameter 1 cm parallel to the circle forming the open top of the cone. A diagram representing this information can be seen below.

A sphere of ice cream, with radius r, is placed on top of the cone. It can be assumed that when the ice cream melts it will run into the cone and not down the sides until the cone is full and overflows.

Find the radius r that the sphere of ice cream must have in order for it to fill the space inside the cone perfectly when melted, leaving no empty space and not overflowing.

A spherical ball bearing of radius 4 mm is fired onto a vertical surface made of soft clay and is embedded to a depth of 2.3 mm. The shape of the ball bearing is not distorted by the impact.

A spherical cap is a portion of a sphere cut off with a plane, as can be seen in the diagram below.

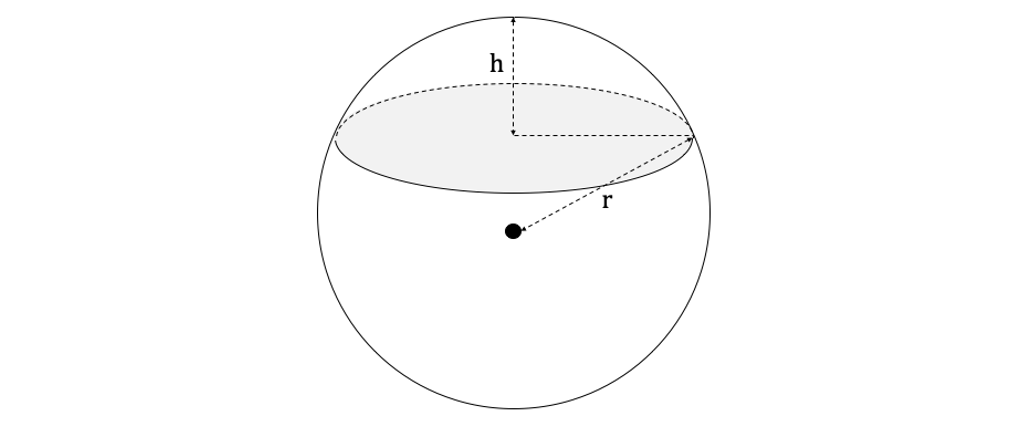
The volume of a spherical cap can be calculated using the following formula: 

where  is the radius of the sphere and  is the height of the spherical cap.

Calculate the volume of soft clay that is displaced by the ball bearing.

Find the angle between the plane forming the cap and the radius connecting the centre of the sphere to the point where the plane intersects the surface of the sphere.

A second ball bearing is fired at the soft clay surface and is embedded to a depth of 2.8 mm. The volume of soft clay that is displaced is the same as it is in part (a).

Find the surface area of the second ball bearing.