Differentiating Special Functions (DP IB Applications & Interpretation (AI)): Revision Note
Did this video help you?
Differentiating trig functions
How do I differentiate sin, cos and tan?
The derivative of
is
The derivative of
is
The derivative of
is
This result for
can be derived using quotient rule
Examiner Tips and Tricks
The derivatives for ,
and
are all given in the formula booklet
For the linear function
, where
and
are constants,
the derivative of
is
the derivative of
is
the derivative of
is
For the general function
,
the derivative of
is
the derivative of
is
the derivative of
is
These last three results can be derived using the chain rule
For calculus with trigonometric functions angles must be measured in radians
Ensure you know how to change the angle mode on your GDC
Examiner Tips and Tricks
As soon as you see a question involving differentiation of trigonometric functions, put your GDC into radians mode.
Worked Example
a) Find for the functions
Answer:

b) A curve has equation.
Find the gradient of the tangent to the curve at the point where .
Give your answer as an exact value.
Answer:
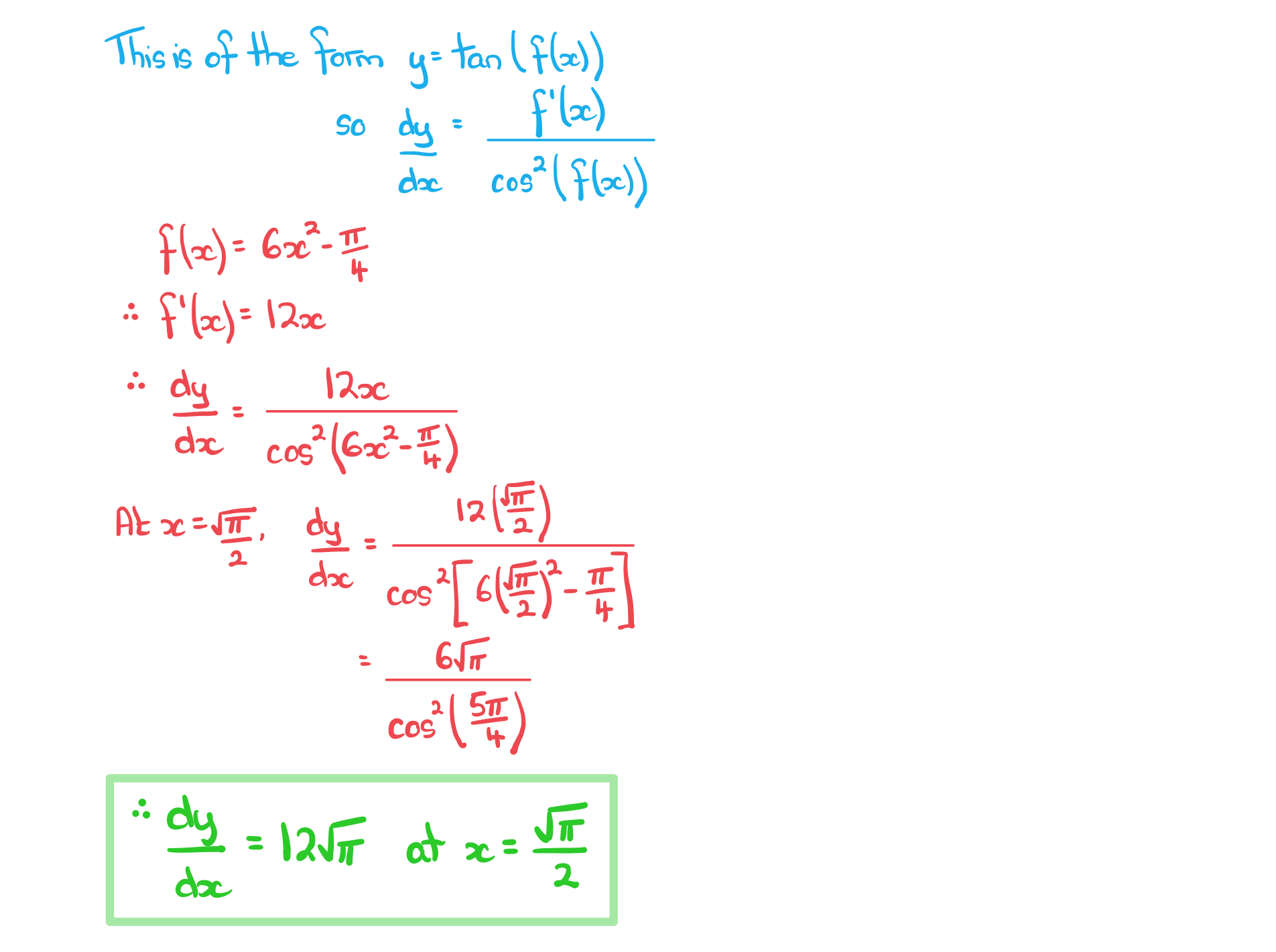
Did this video help you?
Differentiating e^x & lnx
How do I differentiate exponentials and logarithms?
The derivative of
is
where
The derivative of
is
where
For the linear function
, where
and
are constants,
the derivative of
is
the derivative of
is
in the special case
,
(
's cancel)
Examiner Tips and Tricks
Remember to avoid these two common mistakes:
the derivative of
with respect to
is
, NOT
the derivative of
with respect to
is
, NOT
For the general function
,
the derivative of
is
the derivative of
is
The last two sets of results can be derived using the chain rule
Worked Example
A curve has the equation.
Find the gradient of the curve at the point where, giving your answer in the form
, where
and
are integers to be found.
Answer:


Unlock more, it's free!
Did this page help you?