Integrating Special Functions (DP IB Applications & Interpretation (AI)) : Revision Note
Did this video help you?
Integrating Trig Functions
How do I integrate sin, cos and 1/cos2?
The antiderivatives for sine and cosine are
where is the constant of integration
Also, from the derivative of
All three of these standard integrals are in the formula booklet
For the linear function
, where
and
are constants,
For calculus with trigonometric functions angles must be measured in radians
Ensure you know how to change the angle mode on your GDC
Examiner Tips and Tricks
Make sure you have a copy of the formula booklet during revision but don't try to remember everything in the formula booklet
However, do be familiar with the layout of the formula booklet
You’ll be able to quickly locate whatever you are after
You do not want to be searching every line of every page!
For formulae you think you have remembered, use the booklet to double-check
Worked Example
a) Find, in the form, an expression for each integral

b) A curve has equation.
The curve passes through the point with coordinates.
Find an expression for.
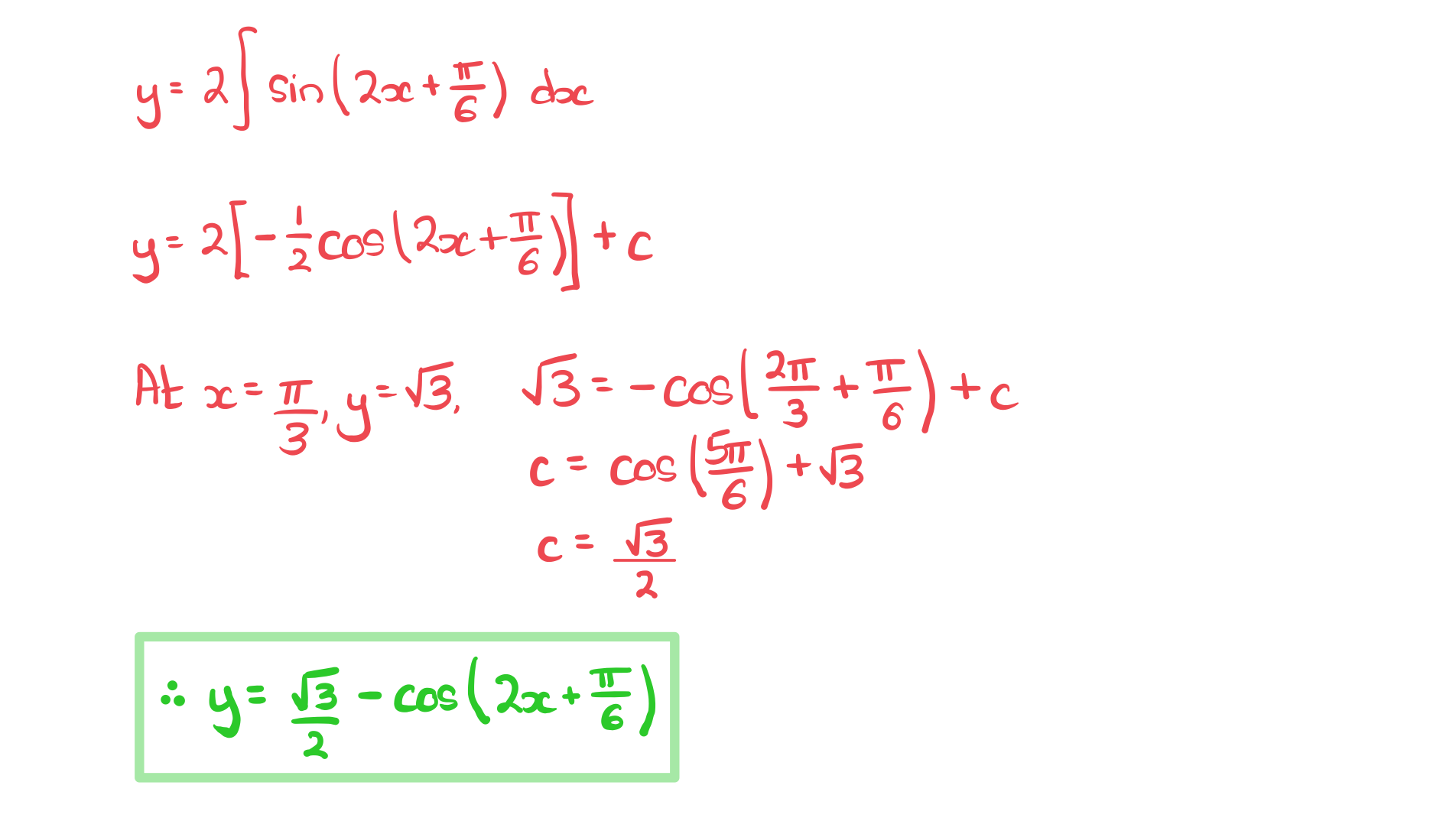
Did this video help you?
Integrating e^x & 1/x
How do I integrate exponentials and 1/x?
The antiderivatives involving
and
are
where is the constant of integration
These are given in the formula booklet
For the linear function
, where
and
are constants,
It follows from the last result that
which can be deduced using Reverse Chain Rule
With ln, it can be useful to write the constant of integration,
, as a logarithm
using the laws of logarithms, the answer can be written as a single term
where
is a constant
This is similar to the special case of differentiating
when
Examiner Tips and Tricks
When revising, familiarise yourself with the layout of this section of the formula booklet, make sure you know what is and isn't in there and how to find it very quickly
Worked Example
A curve has the gradient function.
Given the exact value of is
find an expression for
.
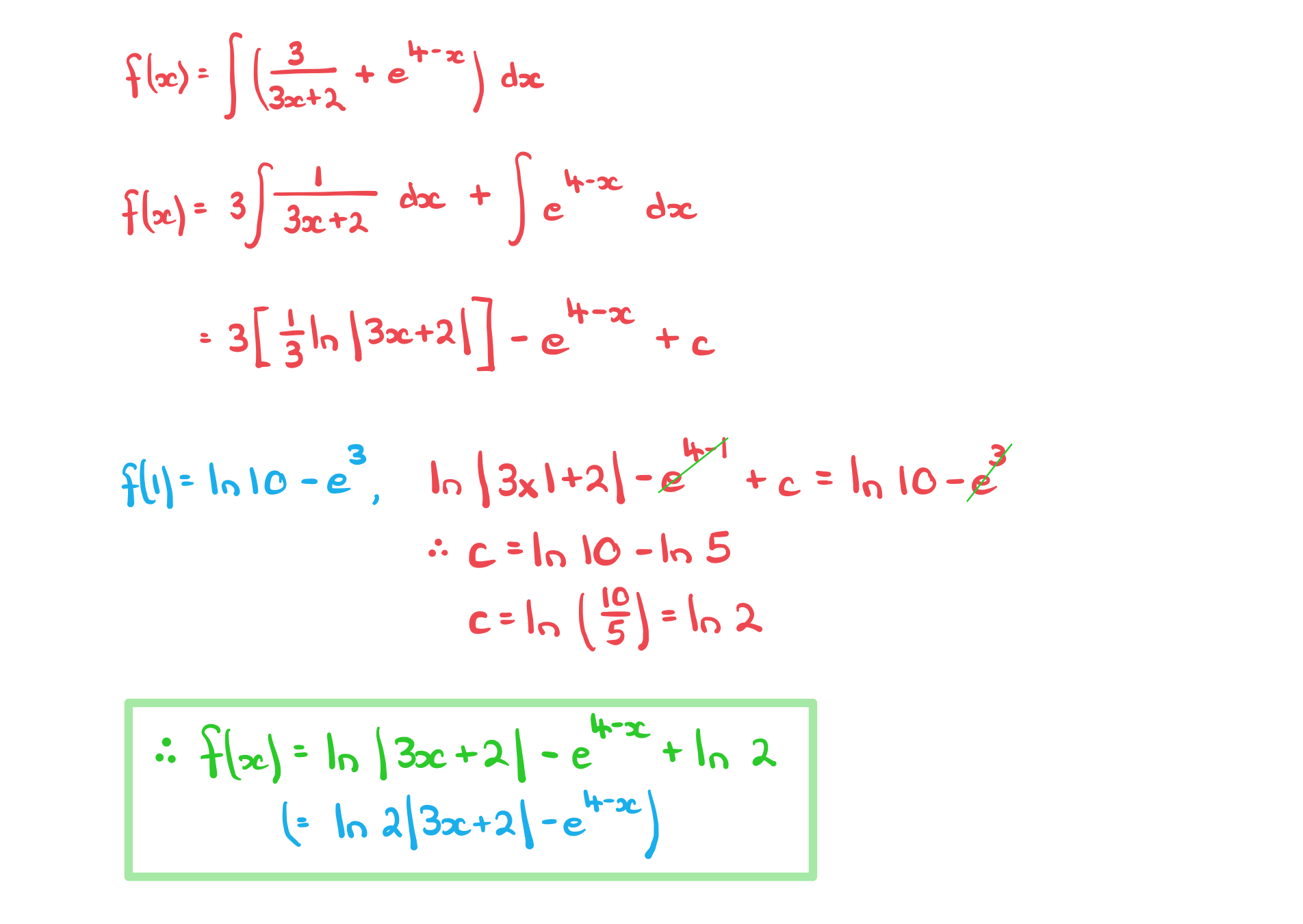

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?
