Calculus for Kinematics | DP IB Maths: AI HL Revision Notes 2021

Did this video help you?

Differentiation for Kinematics

How is differentiation used in kinematics?

Displacement, velocity and acceleration are related by calculus
In terms of differentiation and derivatives
- velocity is the rate of change of displacement
  - $v = \frac{d s}{d t}$ or $v (t) = s' (t)$
- acceleration is the rate of change of velocity
  - $a = \frac{d v}{d t}$ or $a (t) = v' (t)$
- so acceleration is also the second derivative of displacement
  - $a = \frac{d^{2} s}{d t^{2}}$ or $a (t) = s'' (t)$
- Sometimes velocity may be a function of displacement rather than time
  - $v (s)$ rather than $v (t)$
  - in such circumstances, acceleration is $a = v \frac{d v}{d s}$
  - this result is derived from the chain rule
- All acceleration formulae are given in the formula booklet
Even if a motion graph is given, if possible, use your GDC to draw one
- you can then use your GDC’s graphing features to find gradients
  - velocity is the gradient on a displacement (-time) graph
  - acceleration is the gradient on a velocity (-time) graph
Dot notation is often used to indicate time derivatives
- $x$ is sometimes used as displacement (rather than $s$ ) in such circumstances
- $\dot{x} = \frac{d x}{d t}$ , so $\dot{x}$ is velocity
- $\overset{"}{x} = \frac{d^{2} x}{d t^{2}}$ , so $\overset{"}{x}$ is acceleration

Worked example

The displacement,

x

m, of a particle at

t

seconds, is modelled by the function

x (t) = 2 t^{3} - 27 t^{2} + 84 t

Find expressions for

\dot{x}

and

\overset{"}{x}

The velocity,

v

m s^-1, of a particle is given as

v (s) = 6 s - 5 s^{2} - 4

, where

s

m is the displacement of the particle.

Find an expression, in terms of

s

, for the acceleration of the particle.

Did this video help you?

Integration for Kinematics

How is integration used in kinematics?

Since velocity is the derivative of displacement ( $v = \frac{d s}{d t}$ ) it follows that

$s = \int v d t$

Similarly, velocity will be an antiderivative of acceleration

$v = \int a d t$

You might be given the acceleration in terms of the velocity and/or the displacement
- In this case you can solve a differential equation to find an expression for the velocity in terms of the displacement

$a = v \frac{d v}{d s}$

How would I find the constant of integration in kinematics problems?

A boundary or initial condition would need to be known
- phrases involving the word “initial”, or “initially” are referring to time being zero, i.e. $t = 0$
- you might also be given information about the object at some other time (this is called a boundary condition)
- substituting the values in from the initial or boundary condition would allow the constant of integration to be found

How are definite integrals used in kinematics?

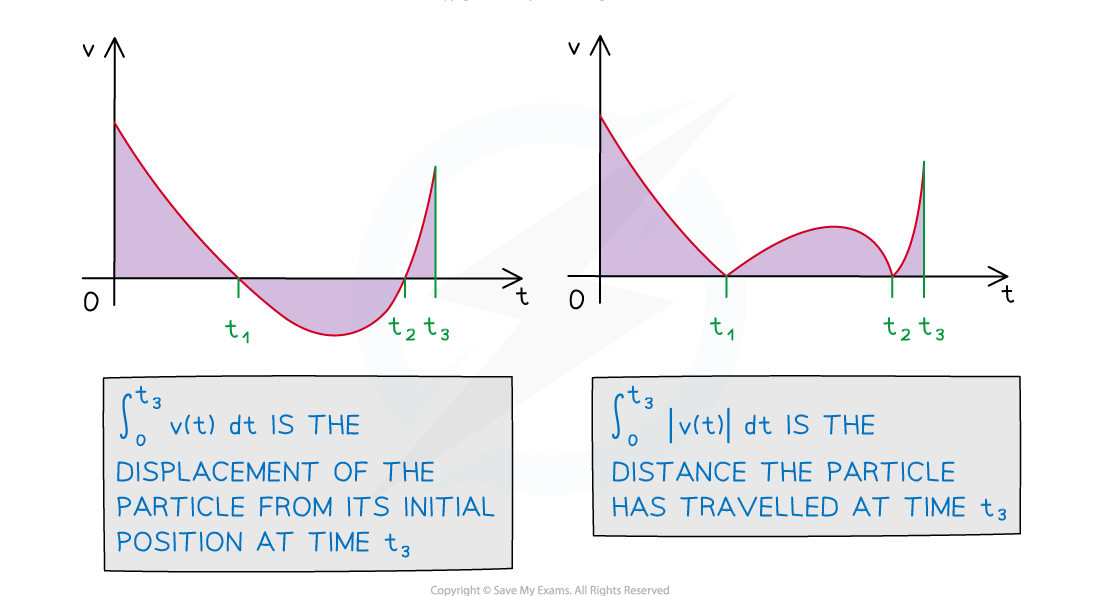
Definite integrals can be used to find the displacement of a particle between two points in time
- $\int_{t_{1}}^{t_{2}} v (t) d t$ would give the displacement of the particle between the times $t = t_{1}$ and $t = t_{2}$
  - This can be found using a velocity-time graph by subtracting the total area below the horizontal axis from the total area above
- $\int_{t_{1}}^{t_{2}} |v (t)| d t$ gives the distance a particle has travelled between the times $t = t_{1}$ and $t = t_{2}$
  - This can be found using a velocity velocity-time graph by adding the total area below the horizontal axis to the total area above
  - Use a GDC to plot the modulus graph $y = |v (t)|$

Two graphs showing the difference between the graph (and integral) of v=v(t) and the graph (and integral) of v=|v(t)|

Examiner Tip

Sketching the velocity-time graph can help you visualise the distances travelled using areas between the graph and the horizontal axis

Worked example

A particle moving in a straight horizontal line has velocity ( $v m s^{- 2}$ ) at time $t$ seconds modelled by $v (t) = 8 t^{3} - 12 t^{2} - 2 t$ .

Given that the initial position of the particle is at the origin, find an expression for its displacement from the origin at time $t$ seconds.
Find the displacement of the particle from the origin in the first five seconds of its motion.
Find the distance travelled by the particle in the first five seconds of its motion.

5-6-2-ib-sl-aa-only-int-kin-we-soltn

Calculus for Kinematics (DP IB Maths: AI HL)

Revision Note

Differentiation for Kinematics

How is differentiation used in kinematics?

Worked example

Integration for Kinematics

How is integration used in kinematics?

How would I find the constant of integration in kinematics problems?

How are definite integrals used in kinematics?

Examiner Tip

Worked example

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Paul