Hypothesis Testing for Mean (Two Sample) (DP IB Maths: AI HL)

Revision Note

Test yourself Flashcards

Author

Dan

Last updated

28 August 2023

Did this video help you?

Two-Sample Tests

What is a two-sample test?

A two-sample test is used to compare the means (μ₁& μ₂) of two normally distributed populations

You use a z-test when the population variances ( $σ_{1}^{2}$ & $σ_{2}^{2}$ ) are known
You use a t-test when the population variances are unknown

In this course you will assume the variances are equal and use a pooled sample for a t-test
In a pooled sample the data from both samples are used to estimate the population variance

What are the steps for performing a two-sample test on my GDC?

STEP 1: Write the hypotheses

H₀: μ₁= μ₂

Clearly state that μ₁& μ₂ represent the population means
Make sure you make it clear which mean corresponds to which population
In words this means that the two population means are equal

For a one-tailed test H₁: μ₁< μ₂ or H₁: μ₁> μ₂
For a two-tailed test: H₁: μ₁ ≠ μ₂

The alternative hypothesis will depend on what is being tested

STEP 2: Decide if it is a z-test or a t-test

If the populations variances are known then use a z-test
If the populations variances are unknown then use a t-test

Assume the variances are equal and use a pooled sample

STEP 3: Enter the data into your GDC and choose two-sample z-test or two-sample t-test

If you have the raw data

Enter the data as a list
Enter the values of σ₁ & σ₂ if a z-test
Choose the pooled option if a t-test

If you have summary statistics (only for a z-test)

Enter the values of ${\bar{x}}_{1}$ , ${\bar{x}}_{2}$ , σ₁, σ₂, n₁ & n₂

Your GDC will give you the p-value

STEP 4: Decide whether there is evidence to reject the null hypothesis

If the p-value < significance level then reject H₀

STEP 5: Write your conclusion

If you reject H₀ then there is evidence to suggest that...

The mean of the 1^st population is smaller (for H₁: μ₁< μ₂)
The mean of the 1^st population is bigger (for H₁: μ₁> μ₂)
The means of the two populations are different (for H₁: μ₁≠ μ₂)

If you accept H₀then there is insufficient evidence to reject the null hypothesis which suggests that...

The mean of the 1^st population is not smaller (for H₁: μ₁< μ₂)
The mean of the 1^st population is not bigger (for H₁: μ₁> μ₂)
The means of the two populations are not different (for H₁: μ₁≠ μ₂)

Worked example

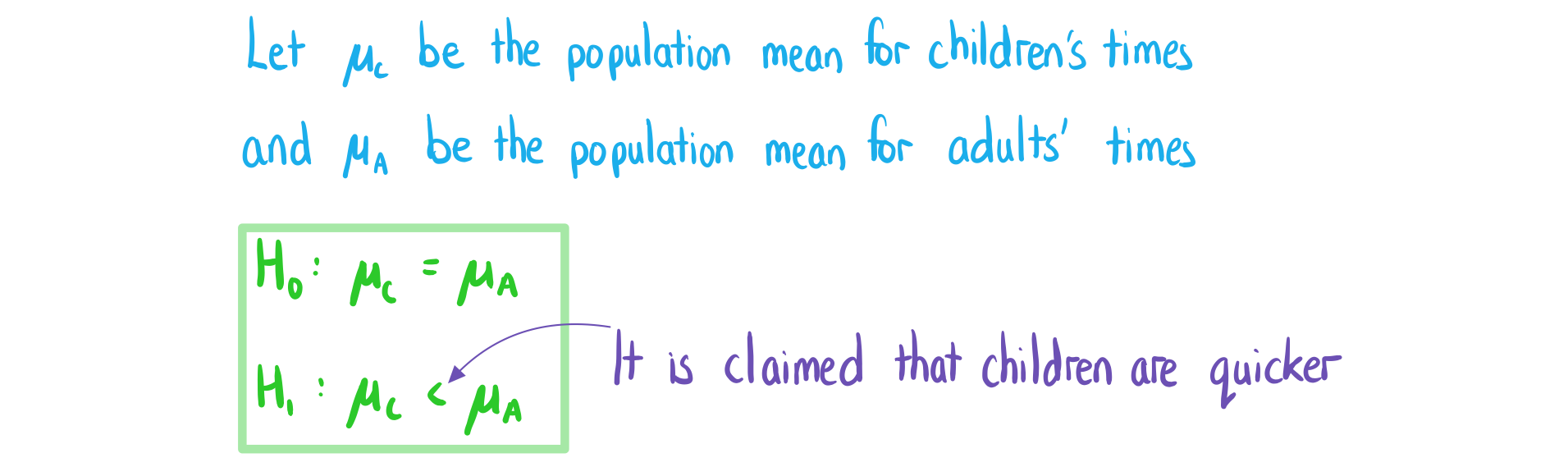
The times (in minutes) for children and adults to complete a puzzle are recorded below.

Children	3.1	2.7	3.5	3.1	2.9	3.2	3.0	2.9
Adults	3.1	3.6	3.5	3.6	2.9	3.6	3.4	3.6	3.7	3.0

The creator of the puzzle claims children are generally faster at solving the puzzle than adults. A t-test is to be performed at a 1% significance level.

Write down the null and alternative hypotheses.

4-7-4-ib-ai-sl-t-test-one-tail-a-we-solution

Find the p-value for this test.

4-7-4-ib-ai-sl-t-test-one-tail-b-we-solution

State whether the creator’s claim is supported by the test. Give a reason for your answer.

4-7-4-ib-ai-sl-t-test-one-tail-c-we-solution

Paired t-tests

What is a paired t-test?

A paired test is where you take two samples but each data point from one sample can be paired with a data point from the other sample

These are used when one group of members are used twice and the two results for each member are paired

It could be to compare the sample before and after introducing a new factor
It could be to compare the sample under two different conditions

For this test you use the differences between the pairs and treat them as one sample

As the variance of the differences is unlikely to be known you will use a t-test
For a paired test you need to assume the differences are normally distributed

You don’t need to assume the populations are normally distributed

What are the steps for performing a paired t-test on my GDC?

STEP 1: Write the hypotheses

H₀: μ_D= 0

Clearly state that μ_D represents the population mean of the differences
In words this means the population mean has not changed

For a one-tailed test H₁: μ_D< 0 or H₁: μ_D> 0
For a two-tailed test: H₁: μ_D ≠ 0

The alternative hypothesis will depend on what is being tested

STEP 2: Enter the data into your GDC and choose the one-sample t-test

Enter the differences as a list

Be consistent with the order in which you subtract paired values

Your GDC will give you the p-value

STEP 3: Decide whether there is evidence to reject the null hypothesis

If the p-value < significance level then reject H₀

STEP 4: Write your conclusion

If you reject H₀ then there is evidence to suggest that...

The mean has decreased (for H₁: μ_D< 0)
The mean has increased (for H₁: μ_D> 0)
The mean has changed (for H₁: μ_D≠ 0)

If you accept H₀then there is insufficient evidence to reject the null which suggests that...

The mean has not decreased (for H₁: μ_D< 0)
The mean has not increased (for H₁: μ_D> 0)
The mean has not changed (for H₁: μ_D≠ 0)

Examiner Tip

If an exam question has two samples with the same number of members then consider carefully whether it makes sense to do a paired test or a two sample test
The examiner might make it look like it is a paired test to trick you!

Worked example

In a school all students must study French and Spanish. 9 students are selected and complete a test in both subjects, the standardised scores are shown below

Student	1	2	3	4	5	6	7	8	9
French score	61	82	77	80	99	69	75	71	81
Spanish score	74	79	83	66	95	79	82	81	85

The headteacher wants to investigate whether there is a difference in the students’ scores between the two subjects. A paired t-test is to be performed at a 10% significance level.

Write down the null and alternative hypotheses.

4-12-2-ib-ai-hl-paired-t-test-a-we-solution