Revision NotesExam QuestionsFlashcards
IBMaths: AI HLDPRevision Notes3. Geometry & Trigonometry3.7 Vector Properties3.7.2 Position & Displacement Vectors

Position & Displacement Vectors (DP IB Maths: AI HL)

Revision Note

Amber

Author

Amber

Last updated

Did this video help you?

Adding & Subtracting Vectors

How are vectors added and subtracted numerically?

  • To add or subtract vectors numerically simply add or subtract each of the corresponding components
  • In column vector notation just add the top, middle and bottom parts together
    • For example: begin mathsize 16px style open parentheses fraction numerator 2 over denominator table row 1 row cell negative 5 end cell end table end fraction close parentheses minus open parentheses fraction numerator 1 over denominator table row 4 row 3 end table end fraction close parentheses equals blank open parentheses fraction numerator 1 over denominator table row cell negative 3 end cell row cell negative 8 end cell end table end fraction close parentheses end style
  • In base vector notation add each of the i, j, and k components together separately
    • For example: (2i + j – 5k) – (i + 4j + 3k) = (i – 3j – 8k)
       

Vector Addition Diagram 1b

How are vectors added and subtracted geometrically?

  • Vectors can be added geometrically by joining the end of one vector to the start of the next one
  • The resultant vector will be the shortest route from the start of the first vector to the end of the second
    • A resultant vector is a vector that results from adding or subtracting two or more vectors
  • If the two vectors have the same starting position, the second vector can be translated to the end of the first vector to find the resultant vector
    • This results in a parallelogram with the resultant vector as the diagonal
  •  To subtract vectors, consider this as adding on the negative vector
    • For example: a – b = a + (-b)
    • The end of the resultant vector a – b will not be anywhere near the end of the vector b
      • Instead, it will be at the point where the end of the vector -b would be

Vector Addition Diagram 1a

Examiner Tip

  • Working in column vectors tends to be easiest when adding and subtracting
    • in your exam, it can help to convert any vectors into column vectors before carrying out calculations with them
  • If there is no diagram, drawing one can be helpful to help you visualise the problem

Worked example

Find the resultant of the vectors a = 5i – 2j and b = begin mathsize 16px style open parentheses fraction numerator negative 3 over denominator table row 1 row 2 end table end fraction close parentheses end style.

3-9-2-ib-aa-hl-add--sub-vectors-we-solution-a-

Did this video help you?

Position Vectors

What is a position vector?

  • A position vector describes the position of a point in relation to the origin
    • It describes the direction and the distance from the point O: 0i + 0j + 0k or  begin mathsize 16px style open parentheses fraction numerator 0 over denominator table row 0 row 0 end table end fraction close parentheses end style
    • It is different to a displacement vector which describes the direction and distance between any two points
  • The position vector of point A is written with the notation a = OA with rightwards arrow on top 
    • The origin is always denoted O
  • The individual components of a position vector are the coordinates of its end point
    • For example the point with coordinates (3, -2, -1) has position vector 3i – 2j – k

Worked example

Determine the position vector of the point with coordinates (4, -1, 8).

3-9-2-ib-aa-hl-position-vector-we-solution

Did this video help you?

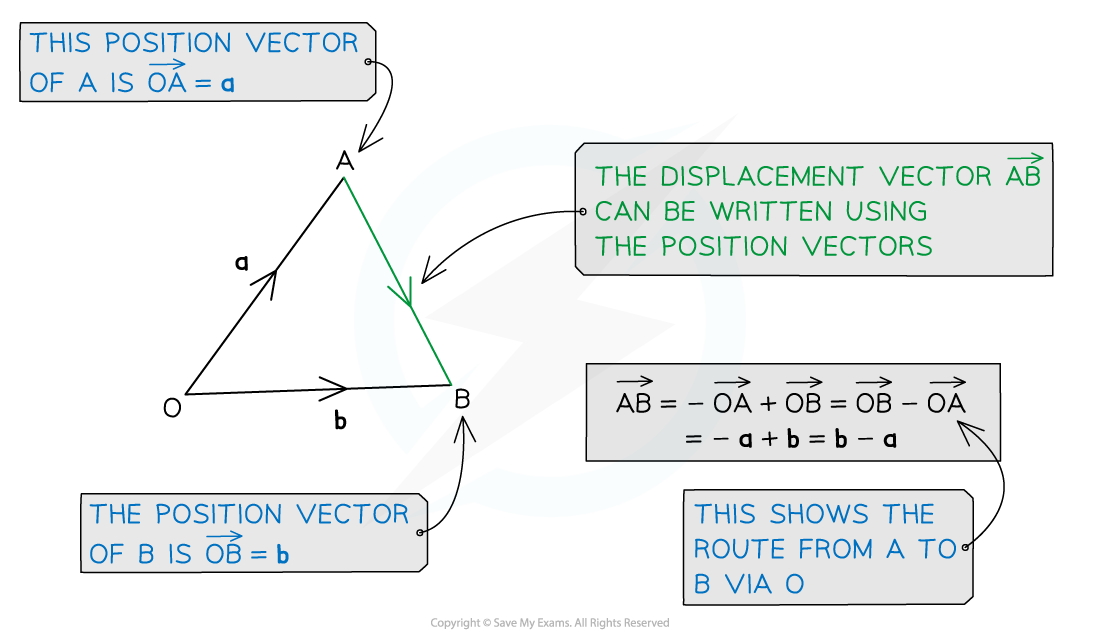
Displacement Vectors

What is a displacement vector?

  • A displacement vector describes the shortest route between any two points
    • It describes the direction and the distance between any two points
    • It is different to a position vector which describes the direction and distance from the point O: 0i + 0j or begin mathsize 16px style open parentheses 0 over 0 close parentheses end style
  • The displacement vector of point B from the point A is written with the notation AB with rightwards arrow on top  
  • A displacement vector between two points can be written in terms of the displacement vectors of a third point
    • AB with rightwards arrow on top equals AC with rightwards arrow on top plus CB with rightwards arrow on top
  • A displacement vector can be written in terms of its position vectors
    •  For example the displacement vector AB with rightwards arrow on top can be written in terms of OA with rightwards arrow on top and OB with rightwards arrow on top
    • AB with rightwards arrow on top equals blank stack AO blank with rightwards arrow on top plus blank stack OB blank with rightwards arrow on top equals blank minus blank stack OA blank with rightwards arrow on top plus blank stack OB blank with rightwards arrow on top equals blank stack OB blank with rightwards arrow on top minus blank stack OA blank with rightwards arrow on top  
    • For position vector a = stack OA blank with rightwards arrow on top and b = stack OB blank with rightwards arrow on topthe displacement vector stack AB blank with rightwards arrow on top can be written b – a

3-9-2-ib-aa-hl-displacement-vectors-diagram-1

Examiner Tip

  • In an exam, sketching a quick diagram can help to make working out a displacement vector easier

Worked example

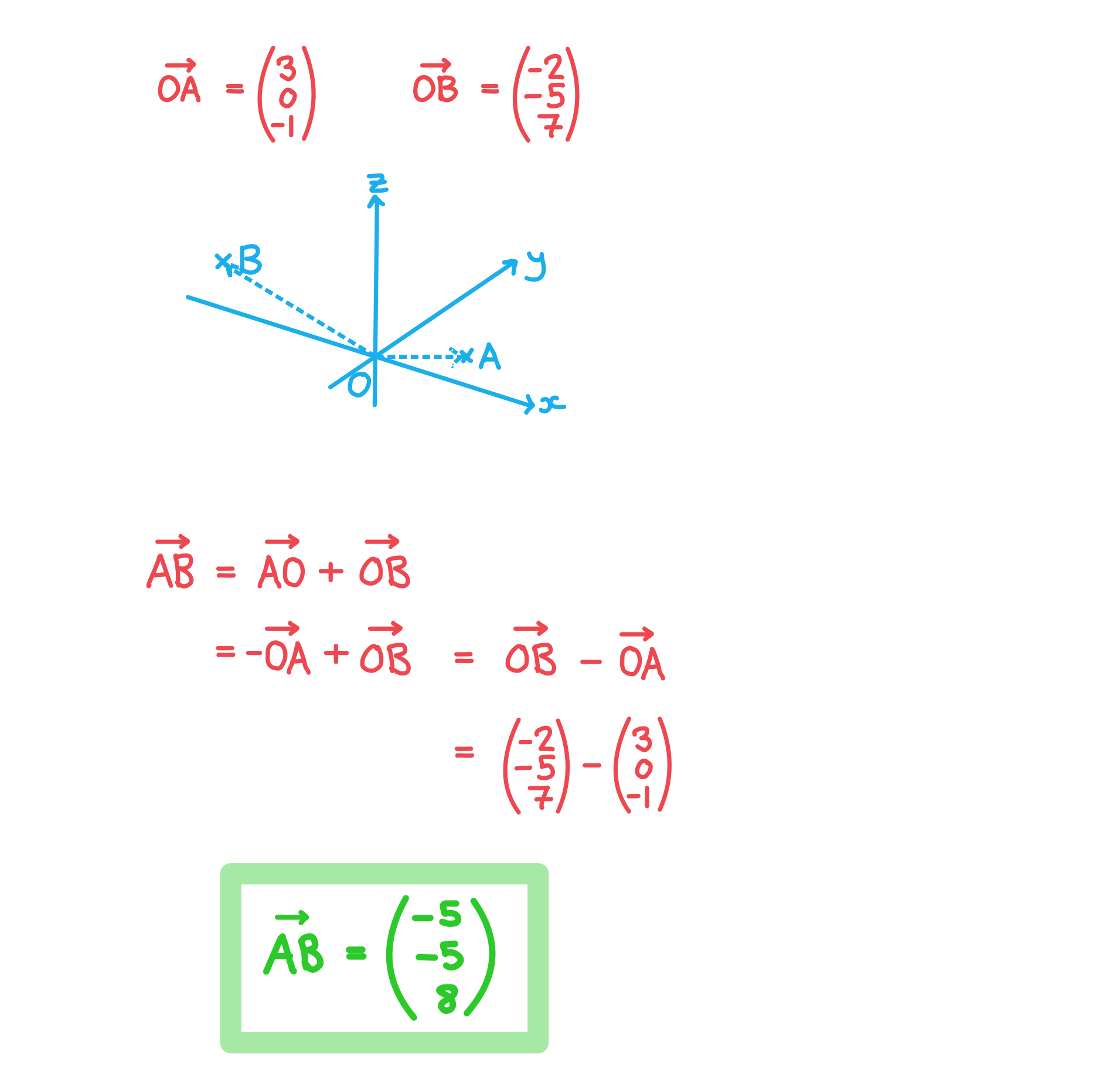
The point A has coordinates (3, 0, -1) and the point B has coordinates (-2, -5, 7). Find the displacement vector AB with rightwards arrow on top.

3-9-2-vectors-we-solution-position-and-displacement-wqe-solution

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards

    Did this page help you?

    Previous:3.7.1 Introduction to VectorsNext:3.7.3 Magnitude of a Vector
    Amber

    Author: Amber

    Expertise: Maths

    Amber gained a first class degree in Mathematics & Meteorology from the University of Reading before training to become a teacher. She is passionate about teaching, having spent 8 years teaching GCSE and A Level Mathematics both in the UK and internationally. Amber loves creating bright and informative resources to help students reach their potential.