Did this video help you?
Solving Trigonometric Equations (DP IB Maths: AI HL): Revision Note
Graphs of Trigonometric Functions
What are the graphs of trigonometric functions?
- The trigonometric functions sin, cos and tan all have special periodic graphs
- You’ll need to know their properties and how to sketch them for a given domain in either degrees or radians
- Sketching the trigonometric graphs can help to
- Solve trigonometric equations and find all solutions
- Understand transformations of trigonometric functions
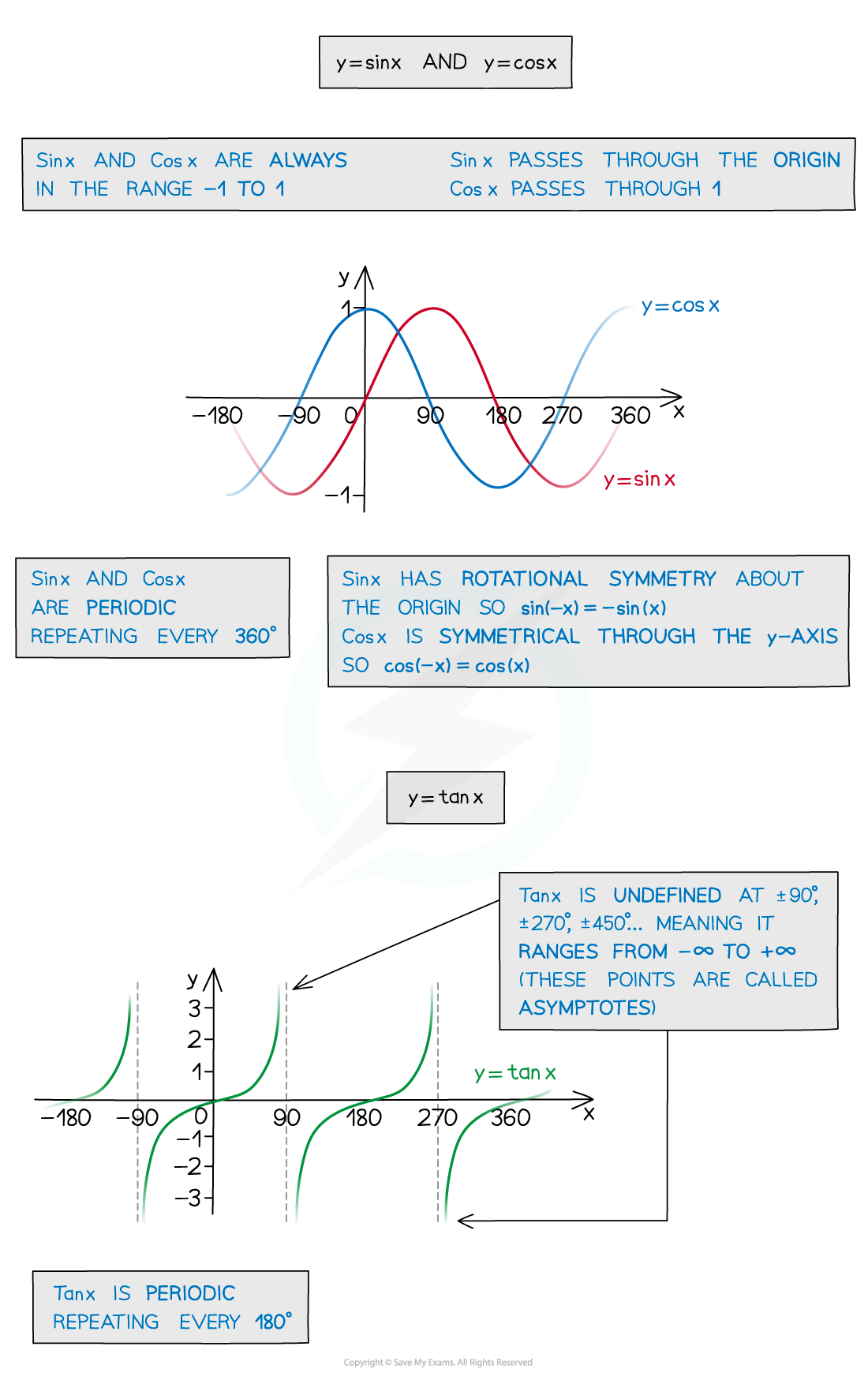
What are the properties of the graphs of sin x and cos x?
- The graphs of sin x and cos x are both periodic
- They repeat every 360° (2π radians)
- The angle will always be on the x-axis
- Either in degrees or radians
- The graphs of sin x and cos x are always in the range -1 ≤ y ≤ 1
- Domain:
- Range:
- The graphs of sin x and cos x are identical however one is a translation of the other
- sin x passes through the origin
- cos x passes through (0, 1)
- Domain:
- The amplitude of the graphs of sin x and cos x is 1
What are the properties of the graph of tan x?
- The graph of tan x is periodic
- It repeats every 180° (π radians)
- The angle will always be on the x-axis
- Either in degrees or radians
- The graph of tan x is undefined at the points ± 90°, ± 270° etc
- There are asymptotes at these points on the graph
- In radians this is at the points ±
, ±
etc
- The range of the graph of tan x is
- Domain:
- Range:
- Domain:
How do I sketch trigonometric graphs?
- You may need to sketch a trigonometric graph so you will need to remember the key features of each one
- The following steps may help you sketch a trigonometric graph
- STEP 1: Check whether you should be working in degrees or radians
- You should check the domain given for this
- If you see π in the given domain then you should work in radians
- STEP 2: Label the x-axis in multiples of 90°
- This will be multiples of
if you are working in radians
- Make sure you cover the whole domain on the x-axis
- This will be multiples of
- STEP 3: Label the y-axis
- The range for the y-axis will be – 1 ≤ y ≤ 1 for sin or cos
- For tan you will not need any specific points on the y-axis
- STEP 4: Draw the graph
- Knowing exact values will help with this, such as remembering that sin(0) = 0 and
cos(0) = 1 - Mark the important points on the axis first
- If you are drawing the graph of tan x put the asymptotes in first
- If you are drawing sin x or cos x mark in where the maximum and minimum points will be
- Try to keep the symmetry and rotational symmetry as you sketch, as this will help when using the graph to find solutions
- Knowing exact values will help with this, such as remembering that sin(0) = 0 and
- STEP 1: Check whether you should be working in degrees or radians
Examiner Tip
- Sketch all three trig graphs on your exam paper so you can refer to them as many times as you need to!
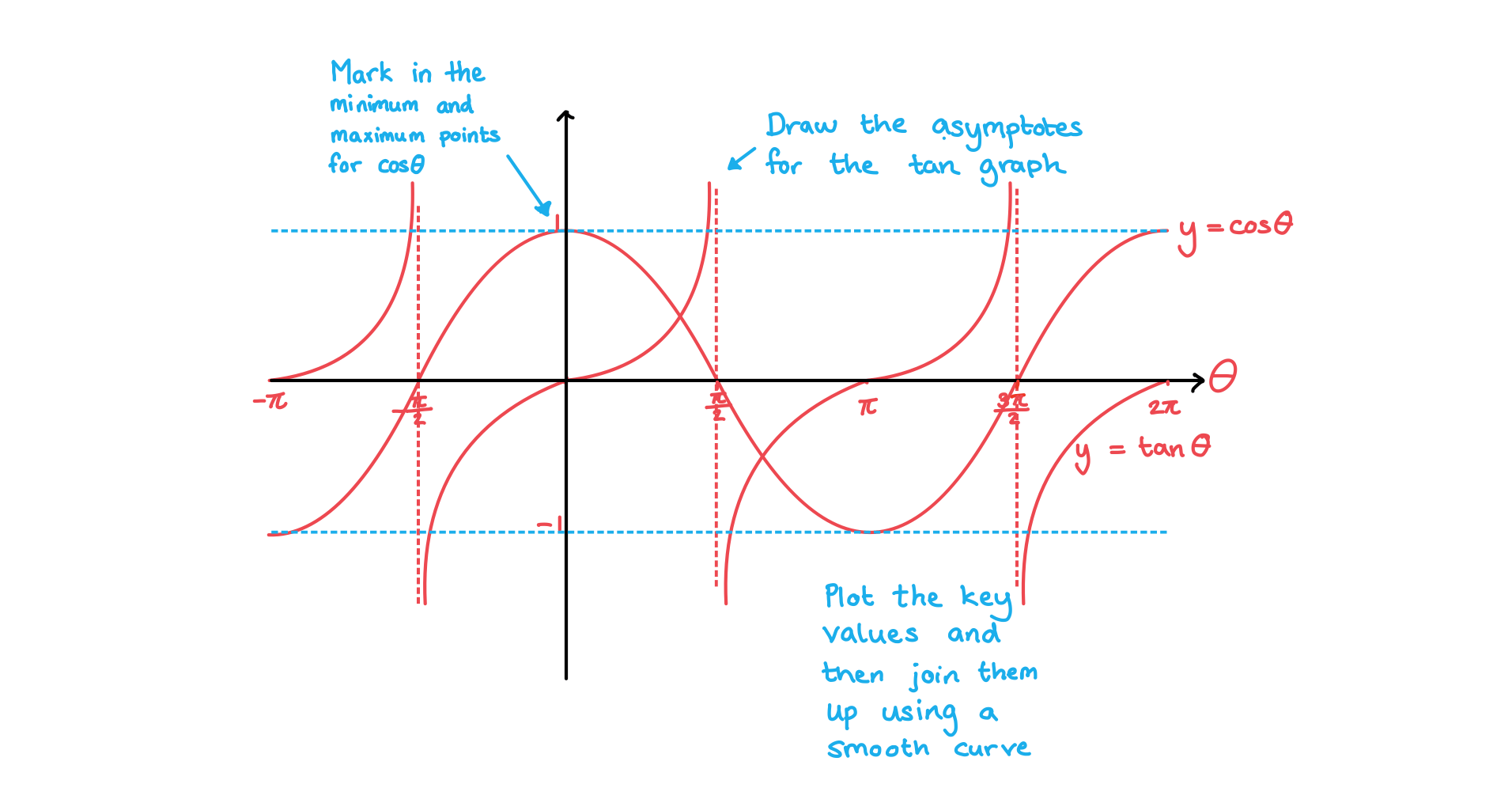
Worked example
Sketch the graphs of y = cosθ and y = tanθ on the same set of axes in the interval -π ≤ θ ≤ 2π. Clearly mark the key features of both graphs.
Did this video help you?
Using Trigonometric Graphs
How can I use a trigonometric graph to find extra solutions?
- Your calculator will only give you the first solution to a problem such as sin-1(0.5)
- This solution is called the primary value
- However, due to the periodic nature of the trig functions there could be an infinite number of solutions
- Further solutions are called the secondary values
- This is why you will be given a domain (interval) in which your solutions should be found
- This could either be in degrees or in radians
- If you see π or some multiple of π then you must work in radians
- This could either be in degrees or in radians
- The following steps will help you use the trigonometric graphs to find secondary values
- STEP 1: Sketch the graph for the given function and interval
- Check whether you should be working in degrees or radians and label the axes with the key values
- STEP 2: Draw a horizontal line going through the y-axis at the point you are trying to find the values for
- For example if you are looking for the solutions to sin-1(-0.5) then draw the horizontal line going through the y-axis at -0.5
- The number of times this line cuts the graph is the number of solutions within the given interval
- STEP 3: Find the primary value and mark it on the graph
- This will either be an exact value and you should know it
- Or you will be able to use your calculator to find it
- STEP 4: Use the symmetry of the graph to find all the solutions in the interval by adding or subtracting from the key values on the graph
- STEP 1: Sketch the graph for the given function and interval
What patterns can be seen from the graphs of trigonometric functions?
- The graph of sin x has rotational symmetry about the origin
- So sin(-x) = - sin(x)
- sin(x) = sin(180° - x) or sin(π – x)
- The graph of cos x has reflectional symmetry about the y-axis
- So cos(-x) = cos(x)
- cos(x) = cos(360° – x) or cos(2π – x)
- The graph of tan x repeats every 180° (π radians)
- So tan(x) = tan(x ± 180°) or tan(x ± π )
- The graphs of sin x and cos x repeat every 360° (2π radians)
- So sin(x) = sin(x ± 360°) or sin(x ± 2π)
- cos(x) = cos(x ± 360°) or cos(x ± 2π)
Examiner Tip
- Take care to always check what the interval for the angle is that the question is focused on
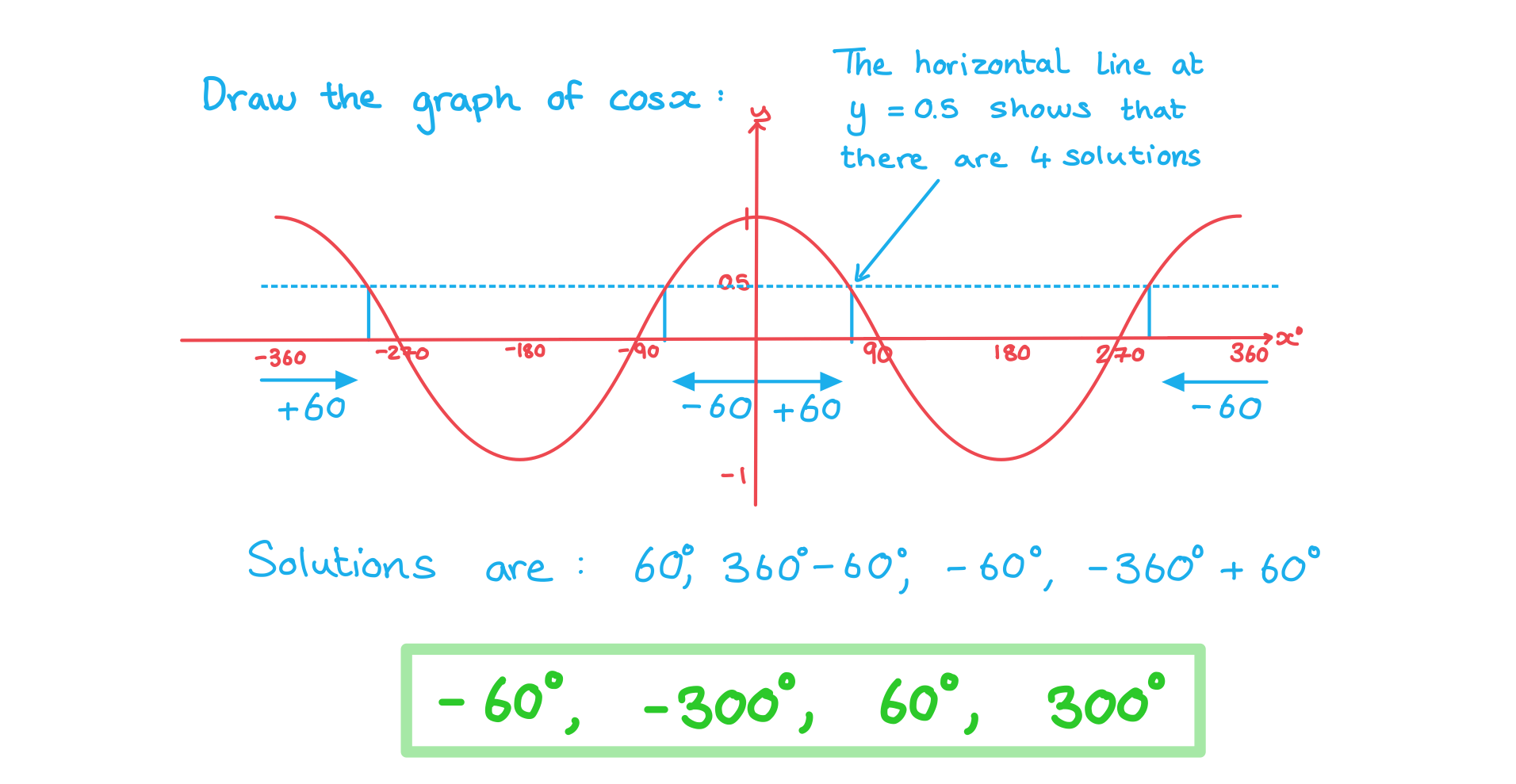
Worked example
One solution to cos x = 0.5 is 60°. Find all the other solutions in the range -360° ≤ x ≤ 360°.

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
