The Unit Circle (DP IB Applications & Interpretation (AI)) : Revision Note
Did this video help you?
Defining Sin, Cos and Tan
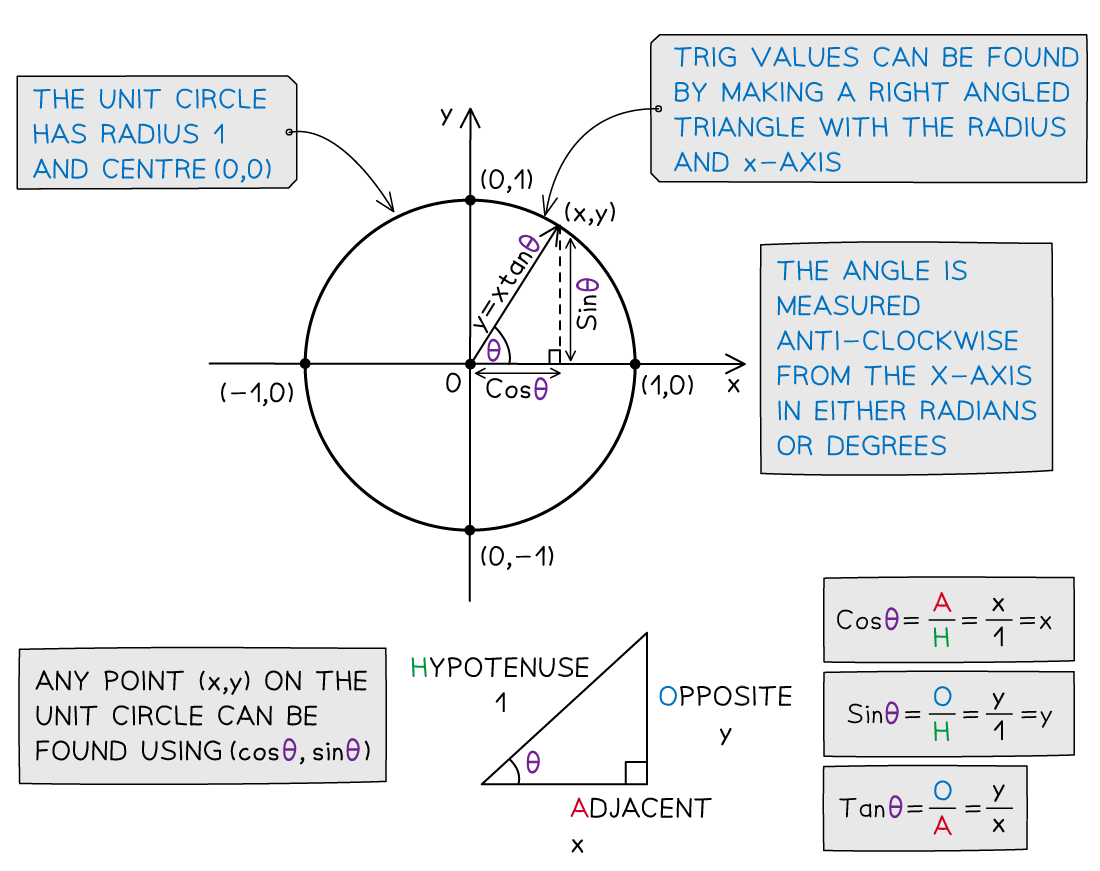
What is the unit circle?
The unit circle is a circle with radius 1 and centre (0, 0)
Angles are always measured from the positive x-axis and turn:
anticlockwise for positive angles
clockwise for negative angles
It can be used to calculate trig values as a coordinate point (x, y) on the circle
Trig values can be found by making a right triangle with the radius as the hypotenuse
θ is the angle measured anticlockwise from the positive x-axis
The x-axis will always be adjacent to the angle, θ
SOHCAHTOA can be used to find the values of sinθ, cosθ and tanθ easily
As the radius is 1 unit
the x coordinate gives the value of cosθ
the y coordinate gives the value of sinθ
As the origin is one of the end points - dividing the y coordinate by the x coordinate gives the gradient
the gradient of the line gives the value of tanθ
It allows us to calculate sin, cos and tan for angles greater than 90° (
rad)
How is the unit circle used to construct the graphs of sine and cosine?
On the unit circle the y-coordinates give the value of sine
Plot the y-coordinate from the unit circle as the y-coordinate on a trig graph for x-coordinates of θ = 0, π/2, π, 3π/2 and 2π
Join these points up using a smooth curve
To get a clearer idea of the shape of the curve the points for x-coordinates of θ = π/4, 3π/4, 5π/4 and 7π/4 could also be plotted
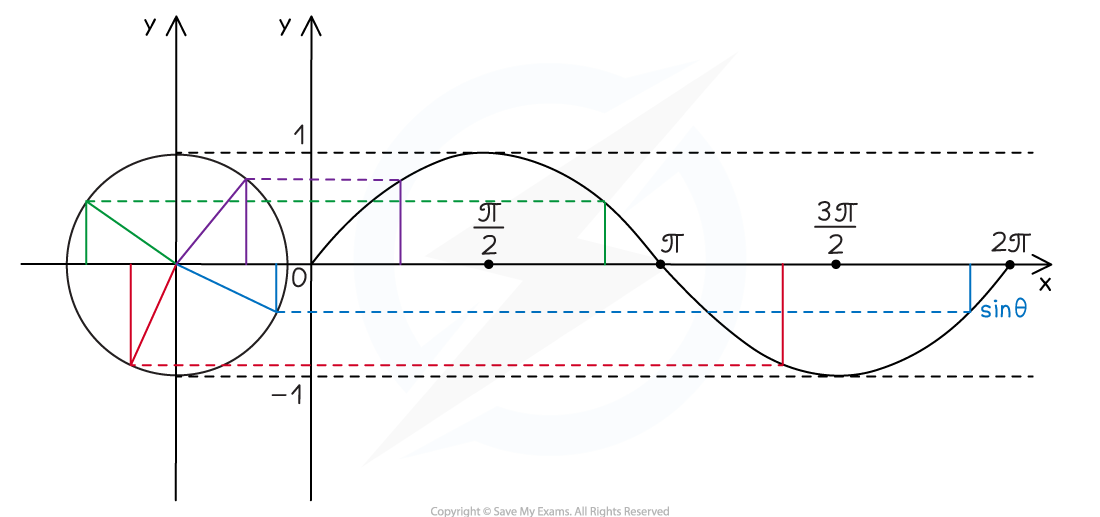
On the unit circle the x-coordinates give the value of cosine
Plot the x-coordinate from the unit circle as the y-coordinate on a trig graph for x-coordinates of θ = 0, π/4, π/2, 3π/4 and 2π
Join these points up using a smooth curve
To get a clearer idea of the shape of the curve the points for x-coordinates of θ = π/4, 3π/4, 5π/4 and 7π/4 could also be plotted

Looking at the unit circle alongside of the sine or cosine graph will help to visualise this clearer
Worked Example
The coordinates of a point on a unit circle, to 3 significant figures, are (0.629, 0.777). Find θ° to the nearest degree.
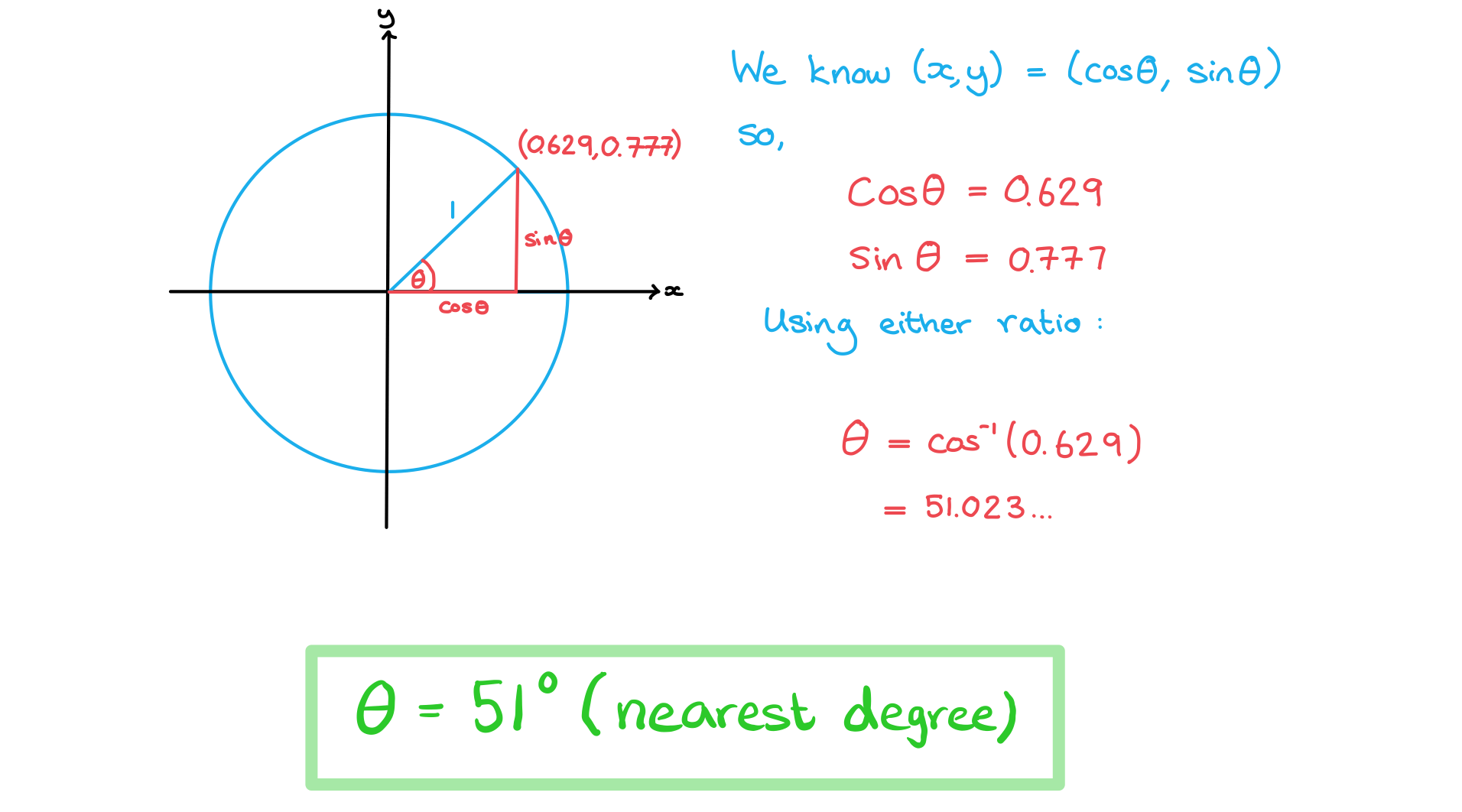
Did this video help you?
Using The Unit Circle
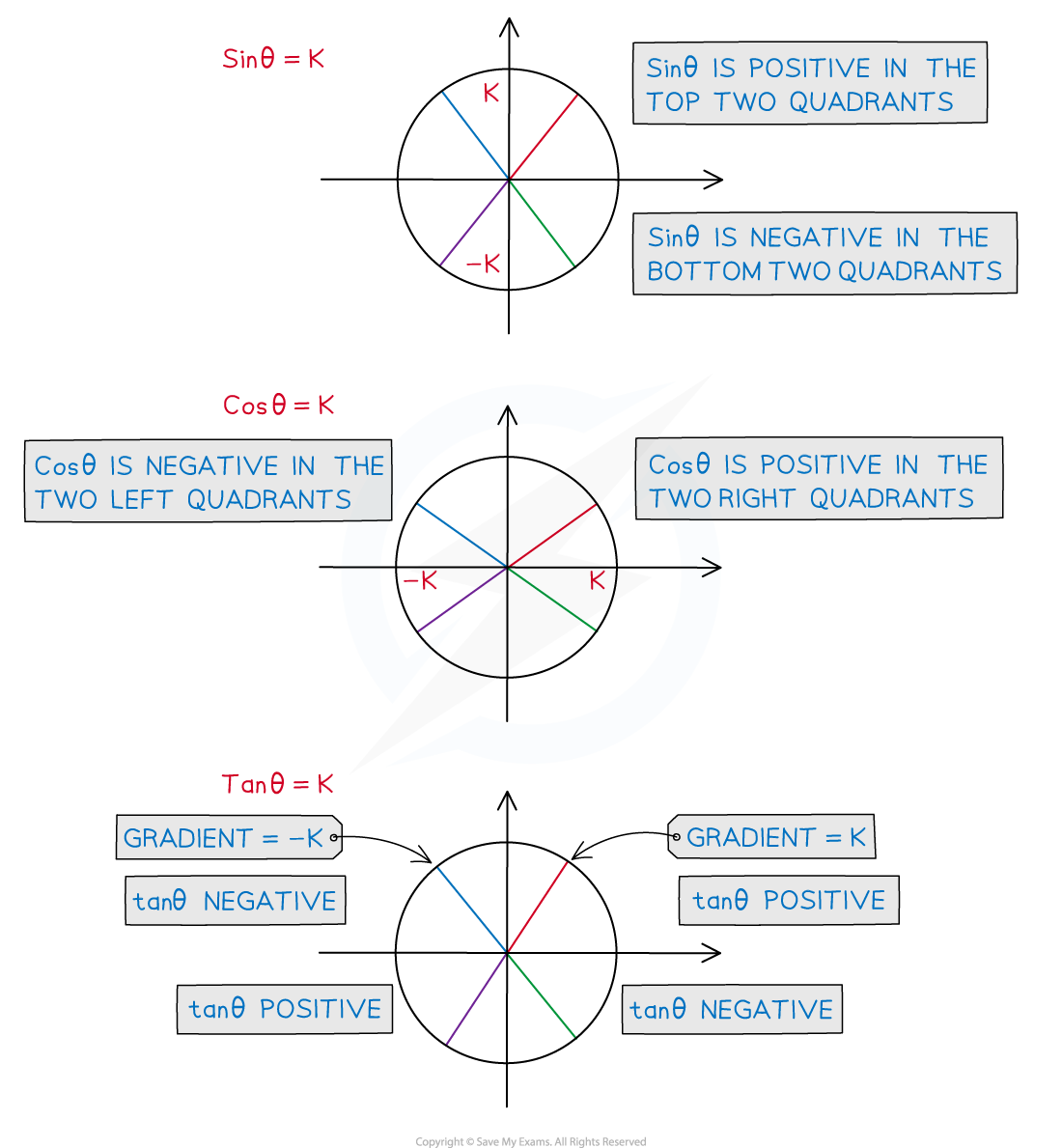
What are the properties of the unit circle?
The unit circle can be split into four quadrants at every 90° (
rad)
The first quadrant is for angles between 0 and 90°
All three of Sinθ, Cosθ and Tanθ are positive in this quadrant
The second quadrant is for angles between 90° and 180° (
rad and
rad)
Sinθ is positive in this quadrant
The third quadrant is for angles between 180° and 270° (
rad and
)
Tanθ is positive in this quadrant
The fourth quadrant is for angles between 270° and 360° (
rad and
)
Cosθ is positive in this quadrant
Starting from the fourth quadrant (on the bottom right) and working anti-clockwise the positive trig functions spell out CAST
This is why it is often thought of as the CAST diagram
You may have your own way of remembering this
A popular one starting from the first quadrant is All Students Take Calculus
To help picture this better try sketching all three trig graphs on one set of axes and look at which graphs are positive in each 90° section
How is the unit circle used to find secondary solutions?
Trigonometric functions have more than one input to each output
For example sin 30° = sin 150° = 0.5
This means that trigonometric equations have more than one solution
For example both 30° and 150° satisfy the equation sin x = 0.5
The unit circle can be used to find all solutions to trigonometric equations in a given interval
Your calculator will only give you the first solution to a problem such as x = sin-1(0.5)
This solution is called the primary value
However, due to the periodic nature of the trig functions there could be an infinite number of solutions
Further solutions are called the secondary values
This is why you will be given a domain in which your solutions should be found
This could either be in degrees or in radians
If you see π or some multiple of π then you must work in radians
The following steps may help you use the unit circle to find secondary values
STEP 1: Draw the angle into the first quadrant using the x or y coordinate to help you
If you are working with sin x = k, draw the line from the origin to the circumference of the circle at the point where the y coordinate is k
If you are working with cos x = k, draw the line from the origin to the circumference of the circle at the point where the x coordinate is k
If you are working with tan x = k, draw the line from the origin to the circumference of the circle such that the gradient of the line is k
Note that whilst this method works for tan, it is complicated and generally unnecessary, tan x repeats every 180° (π radians) so the quickest method is just to add or subtract multiples of 180° to the primary value
This will give you the angle which should be measured from the positive x-axis…
… anticlockwise for a positive angle
… clockwise for a negative angle
STEP 2: Draw the radius in the other quadrant which has the same...
... x-coordinate if solving cos x = k
This will be the quadrant which is vertical to the original quadrant
... y-coordinate if solving sin x = k
This will be the quadrant which is horizontal to the original quadrant
... gradient if solving tan x = k
This will be the quadrant diagonally across from the original quadrant
STEP 3: Work out the size of the second angle, measuring from the positive x-axis
… anticlockwise for a positive angle
… clockwise for a negative angle
You should look at the given range of values to decide whether you need the negative or positive angle
STEP 4: Add or subtract either 360° or 2π radians to both values until you have all solutions in the required range
Examiner Tips and Tricks
Being able to sketch out the unit circle and remembering CAST can help you to find all solutions to a problem in an exam question
Worked Example
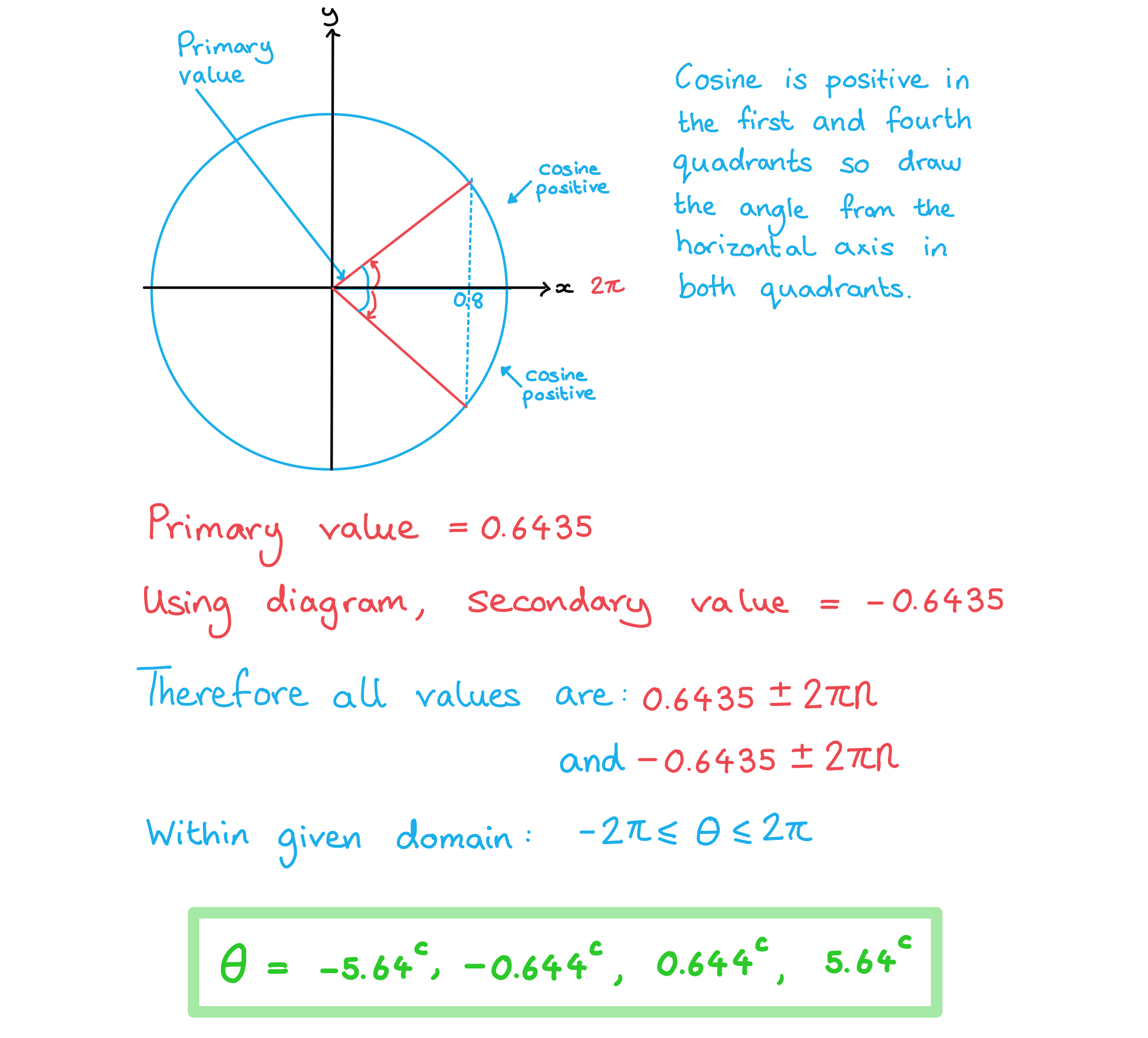
Given that one solution of cosθ = 0.8 is θ = 0.6435 radians correct to 4 decimal places, find all other solutions in the range -2π ≤ θ ≤ 2π. Give your answers correct to 3 significant figures.

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?
