Walks & Adjacency Matrices (DP IB Applications & Interpretation (AI)): Revision Note
Walks & adjacency matrices
What is an adjacency matrix?
An adjacency matrix can be used to represent a graph
It is a square matrix where all the vertices in the graph are listed as the headings for both the rows (
) and columns (
)
The entry
represents the number of edges that go from vertex
to vertex
In a simple graph the only entries are either 0 or 1
The matrix will be symmetrical for an undirected graph
A loop counts as one edge
Examiner Tips and Tricks
Be careful! This is not fully agreed amongst mathematicians. Some people add 2 for every loop. This means that the sum of the entries in a row or column is equal to the degree of the vertex.
However, when counting walks it is best to consider a loop as one walk, unless you clockwise and counter-clockwise directions need to be considered separately.
For a directed graph
The sum of the entries in a row is the out degree of that vertex
The sum of the entries in a column is the in degree of that vertex
A loop always counts as 1 as there is a direction involved
For example, consider
There is 1 edge that start at
and end at
There are 3 edges that start at
and end at
Worked Example
Let G be the graph below.
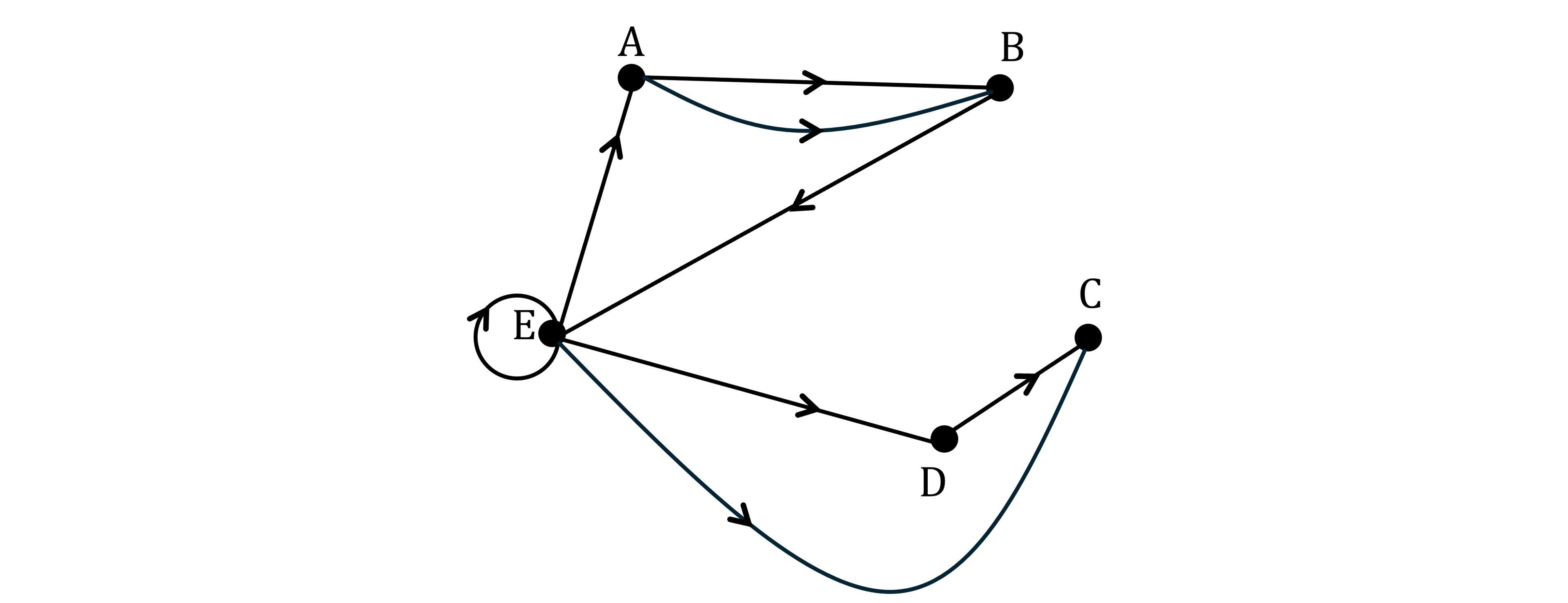
Write down the adjacency matrix for G.
Answer:

Number of walks
What is the length of a walk?
The length of a walk is the number of edges that are traversed
How do I calculate the number of walks between a pair of vertices?
Let
denote the adjacency matrix of a graph
The entries of the adjacency matrix
tells you the number of walks of length 1 between each pair of vertices
The (i, j) entry in the matrix
is the number of 1-length walks from vertex i to vertex j
The entries of the adjacency matrix
tells you the number of walks of length k between each pair of vertices
The (i, j) entry in the matrix
is the number of k-length walks from vertex i to vertex j
Examiner Tips and Tricks
This matrix gives the number of walks that contain exactly k edges.
For example, if
is the adjacency matrix
Then
There are 8 walks from
to
which use exactly 3 edges
If you need to find the total number of walks of at most length n
Calculate
You can denote this
The (i, j) entry in this matrix is the number of walks from vertex i to vertex j of length at most n
Worked Example
The adjacency matrix M of a graph G is given by
a) Draw the graph described by the adjacency matrix M.
Answer:

b) Find the number of walks of length 4 from vertex B to Vertex E.
Answer:

c) Find the number of walks of 3 or less from vertex A to vertex C.
Answer:

Weighted adjacency tables
What is a weighted adjacency table?
A weighted adjacency table is different to an adjacency matrix
The value in each cell is the weight of the edge connecting that pair of vertices
Weight could be cost, distance, time etc.
An empty cell can be used to indicate that there is no connection between a pair of vertices
Weighted adjacency tables can be used to find:
Bounds for the Travelling Salesman Problem
You can construct transition matrices when the weights represent probabilities
Worked Example
The table below shows the time taken in minutes to travel by car between 4 different towns.
| A | B | C | D |
|---|---|---|---|---|
A | - | 16 | 35 | - |
B | 16 | - | 20 | 18 |
C | 35 | 20 | - | 34 |
D | - | 23 | 34 | - |
State the time taken to drive from Town B to Town D.
Answer:


Unlock more, it's free!
Was this revision note helpful?
