Coordinate Geometry (DP IB Applications & Interpretation (AI)): Revision Note
Did this video help you?
Basic coordinate geometry
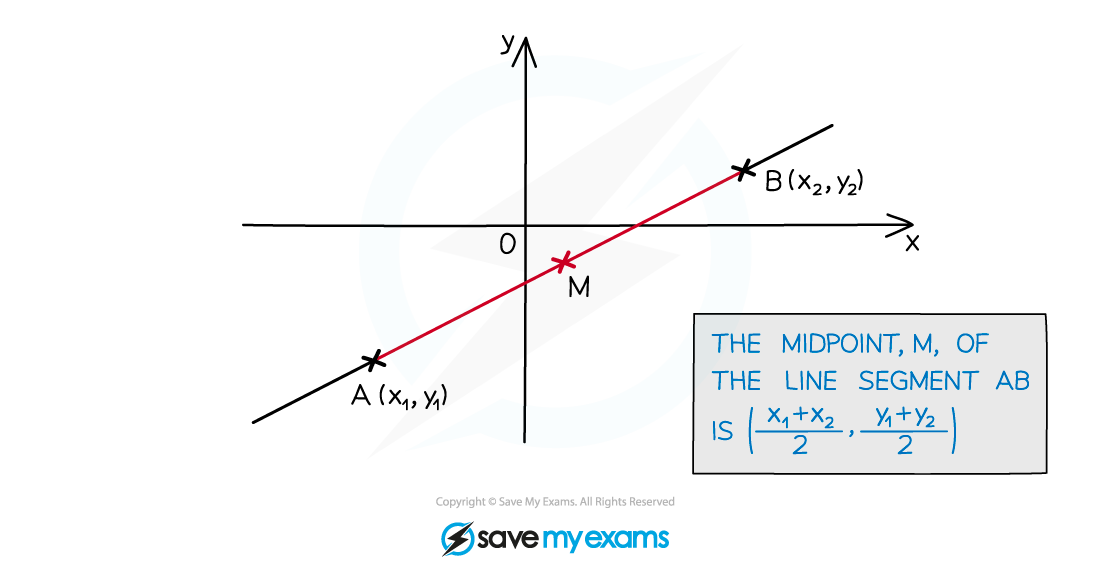
How do I find the midpoint of two points?
The midpoint of two points is the middle point
It lies on the line segment joining the two points together
It is the point that is equidistant from the two points
The coordinates of the midpoint of
and
are
It is just the average of the two coordinates
This is given in the formula booklet under the prior learning section
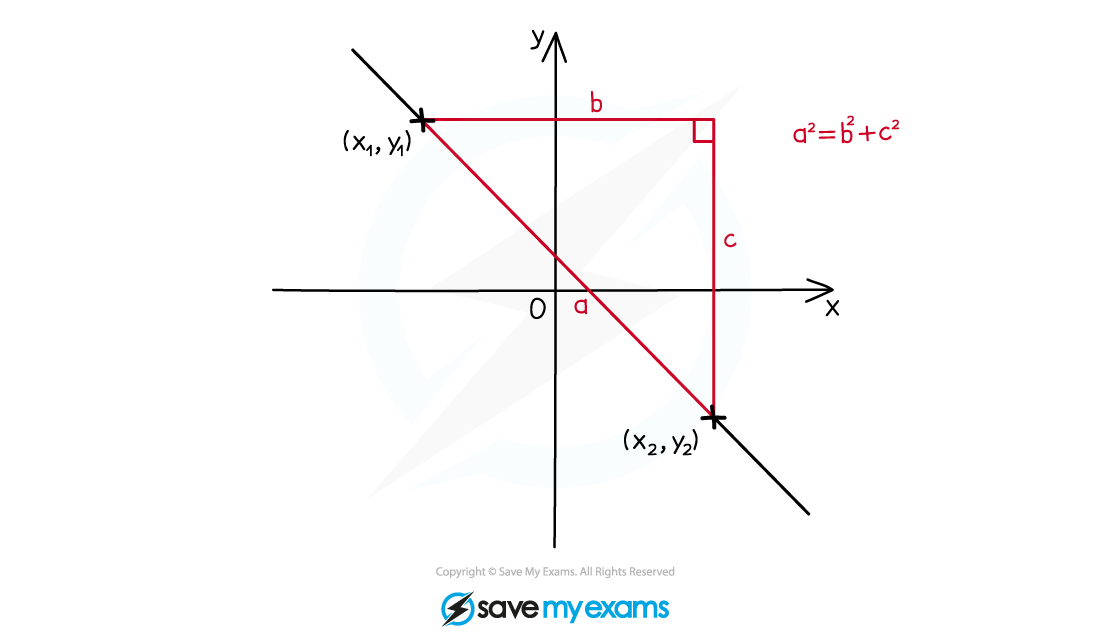
How do I find the distance between two points?
The distance between two points is the length of the line segment joining them
The length of the line segment between
and
is
This is just an application of Pythagoras' Theorem
This is given in the formula booklet under the prior learning section
The line segment between A and B is denoted [AB]
Examiner Tips and Tricks
It does not matter which way around you subtract the numbers because the differences are squared.
How do I find the gradient of the line segment between two points?
The gradient of the line segment between
and
is
This is change in
divided by the change in
This is given in the formula booklet under the functions section
Examiner Tips and Tricks
You can switch around the coordinates in the formula . You just need to make sure that the first
value on the numerator and the first
value on the denominator are part of the same coordinate.
Worked Example
Point A has coordinates (3, -4) and point B has coordinates (-5, 2).
i) Calculate the distance of the line segment AB.

ii) Find the gradient of the line connecting points A and B.

iii) Find the midpoint of [AB ] .

Ready to test your students on this topic?
- Create exam-aligned tests in minutes
- Differentiate easily with tiered difficulty
- Trusted for all assessment types

Did this page help you?