Revision NotesExam QuestionsFlashcardsPast PapersMock Exams
IBMathsDPApplications & Interpretation (AI)HLRevision Notes2. FunctionsModelling with FunctionsDirect & Inverse Variation

Direct & Inverse Variation (DP IB Applications & Interpretation (AI)): Revision Note

Dan Finlay

Written by: Dan Finlay

Reviewed by: Lucy Kirkham

Updated on

DP Applications & Interpretation (AI): HLDP Applications & Interpretation (AI): SL

Direct variation

What is direct variation?

  • Two variables are said to vary directly if their ratio is constant (k)

    • This is also called direct proportion

  • If yand x to the power of n (for positive integer n) vary directly then:

    • It is denoted as y proportional to x to the power of n

    • y equals k x to the power of n for some constant k

      • This can be written as y over x to the power of n equals k

  • The graphs of these models always start at the origin

How do I find the equation of a direct variation model?

  • Identify which two variables vary directly

    • It might not be x and y

    • It could be x cubed and y

  • Use the given information to find their constant ratio k

    • Also called constant of proportionality

    • Substitute the given values of x and y into your formula

    • Solve to find k

  • Write the equation which models their relationship

    • y equals k x to the power of n

  • You can then use the equation to solve problems

Worked Example

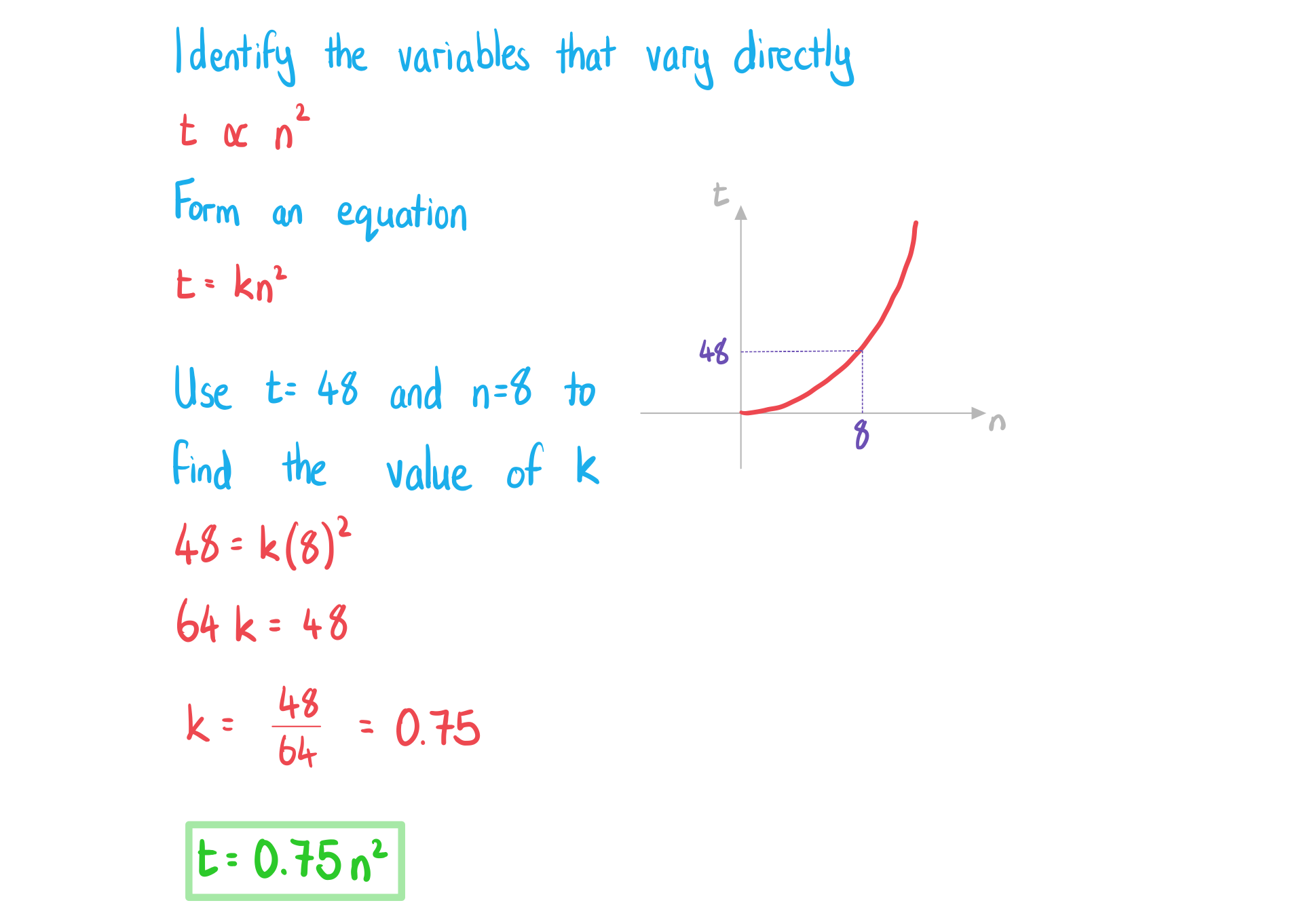
A computer program sorts a list of numbers into ascending order. The time it takes, t milliseconds, varies directly with the square of the number of items, n, in the list. The computer program takes 48 milliseconds to order a list with 8 items.

a) Find an equation connecting t and n.

2-3-4-ib-ai-sl-direct-variation-a-we-solution

b) Find the time it takes to order a list of 50 numbers.

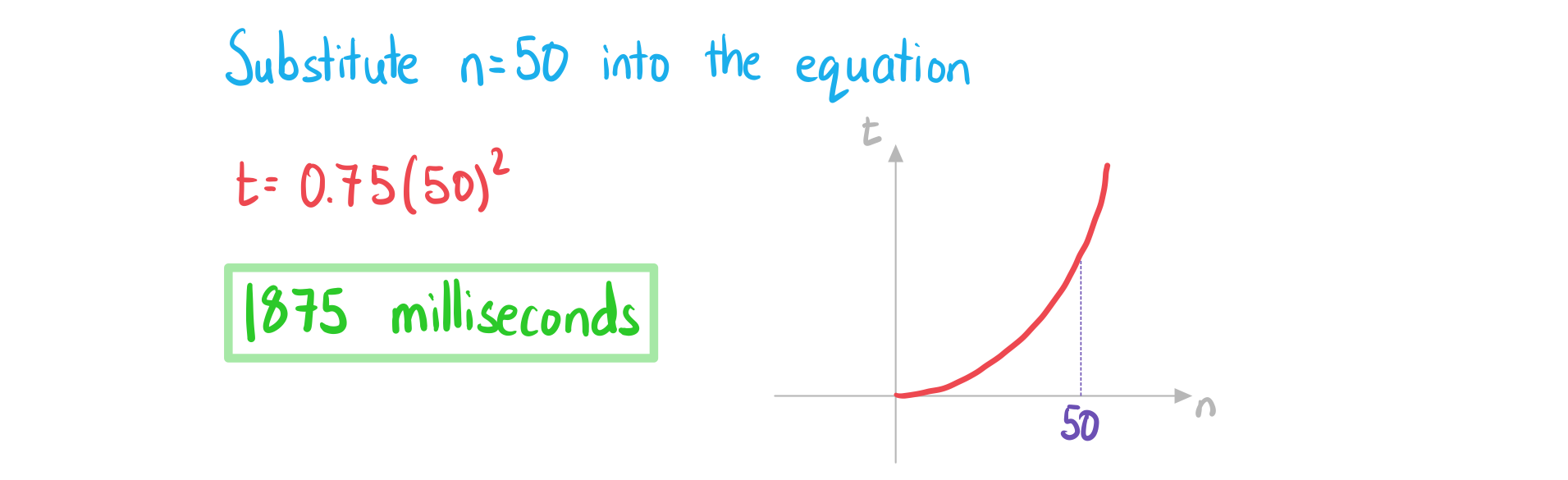
2-3-4-ib-ai-sl-direct-variation-b-we-solution

Inverse variation

What is inverse variation?

  • Two variables are said to vary inversely if their product is constant (k)

    • This is also called inverse proportion

  • If y and x to the power of n (for positive integer n) vary inversely then:

    • It is denoted y proportional to 1 over x to the power of n

    • y equals k over x to the power of n for some constant k

      • This can be written x to the power of n y equals k

  • The graphs of these models all have a vertical asymptote at the y-axis

    • This means that as x gets closer to 0 the absolute value of y gets further away from 0

    • x can never equal 0

  • The graphs of these models all have a horizontal asymptote at the x-axis

    • This means that as x gets large y gets closer to 0

    • y can never equal 0

How do I find the equation of an inverse variation model?

  • Identify which two variables vary inversely

    • It might not be x and y

    • It could be x cubed and y

  • Use the given information to find their constant product k

    • Also called constant of proportionality

    • Substitute the given values of x and y into your formula

    • Solve to find k

  • Write the equation which models their relationship

    • y equals k over x to the power of n

  • You can then use the equation to solve problems

Examiner Tips and Tricks

Reciprocal graphs generally have two parts/curves

  • Only one – usually the positive – may be relevant to the model

  • Think about why x/t/θ can only take positive values - refer to the context of the question

Worked Example

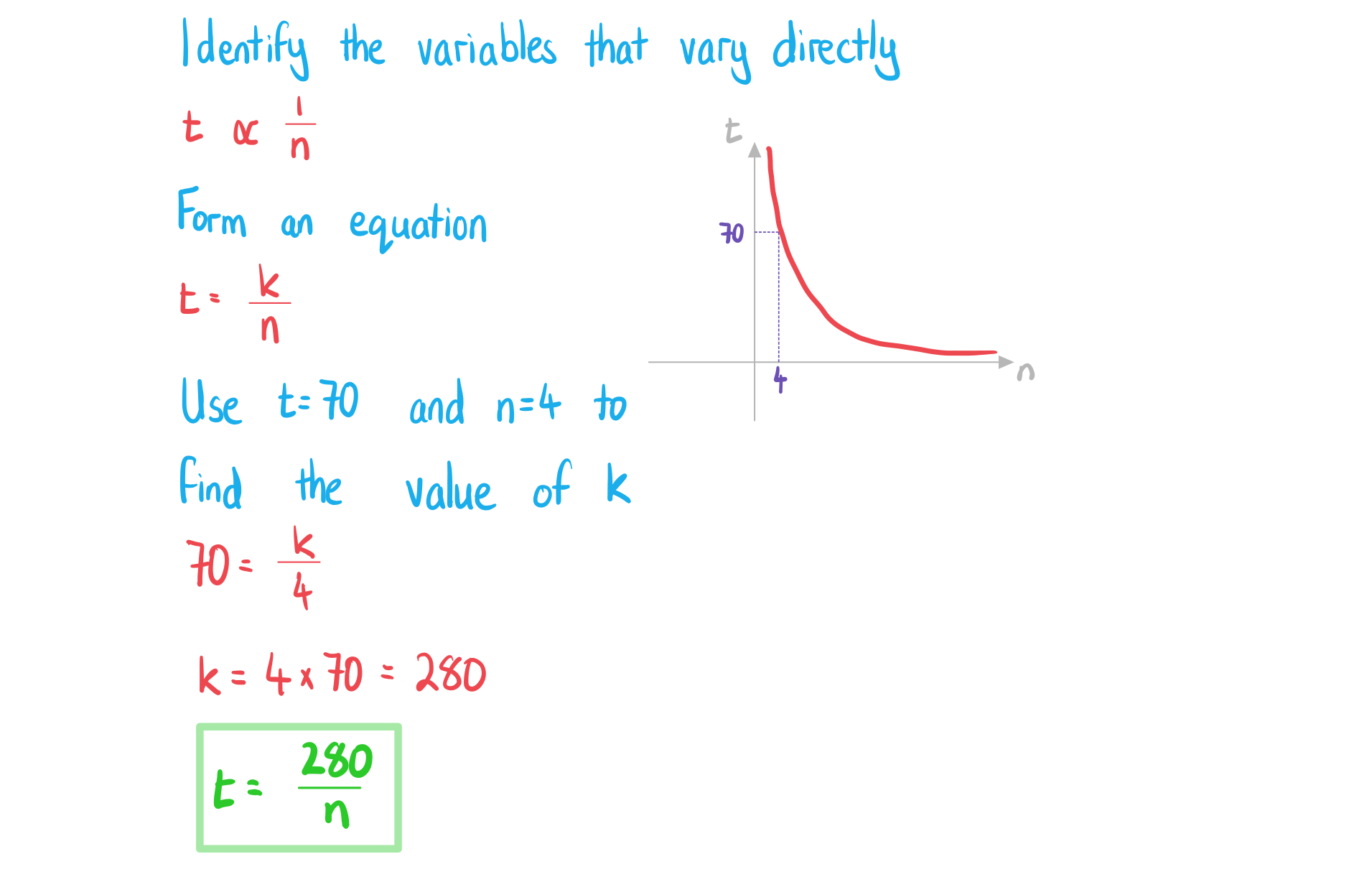
The time, t hours, it takes to complete a project varies inversely to the number of people working on it, n. If 4 people work on the project it takes 70 hours to complete.

a) Write an equation connecting t and n.

2-3-4-ib-ai-sl-inverse-variation-a-we-solution

b) Given that the project needs to be completed within 18 hours, find the minimum number of people needed to work on it.

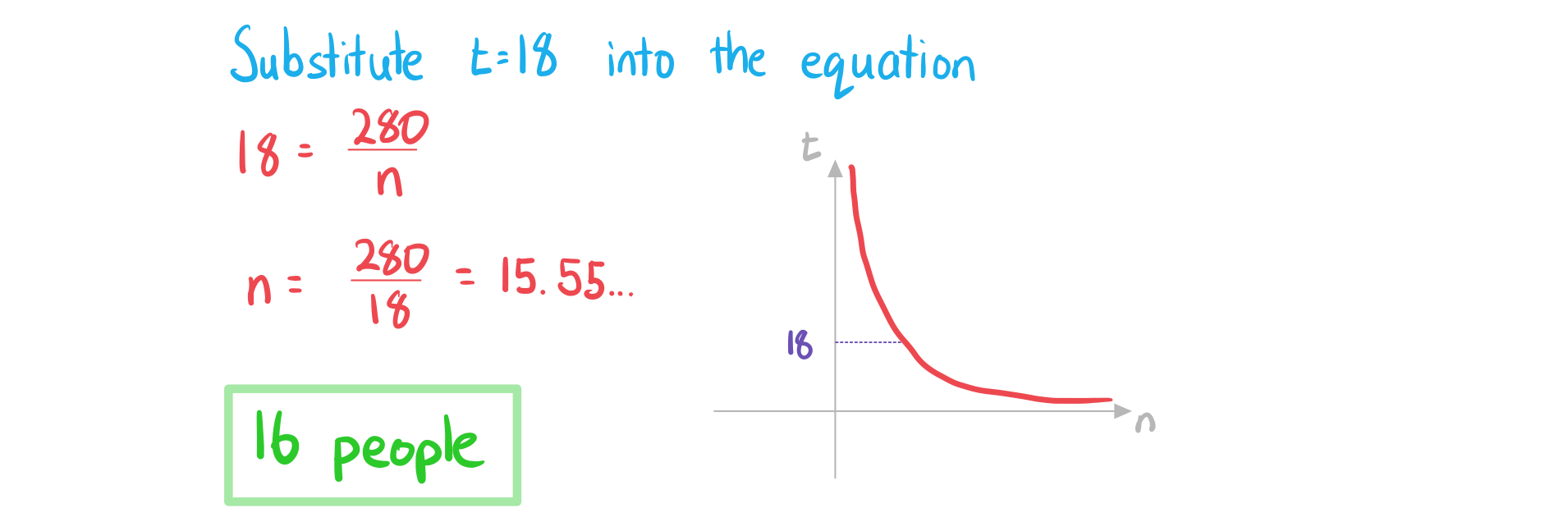
2-3-4-ib-ai-sl-inverse-variation-b-we-solution

You've read 0 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards
    Previous:Exponential ModelsNext:Sinusoidal Models
    Author
    Reviewer
    Dan Finlay

    Author: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.

    Lucy Kirkham

    Reviewer: Lucy Kirkham

    Expertise: Head of Content Creation

    Lucy has been a passionate Maths teacher for over 12 years, teaching maths across the UK and abroad helping to engage, interest and develop confidence in the subject at all levels.Working as a Head of Department and then Director of Maths, Lucy has advised schools and academy trusts in both Scotland and the East Midlands, where her role was to support and coach teachers to improve Maths teaching for all.