Direct & Inverse Variation (DP IB Maths: AI HL)

Revision Note

Test yourself Flashcards

Author

Dan

Last updated

20 June 2023

Did this video help you?

Direct Variation

What is direct variation?

Two variables are said to vary directly if their ratio is constant (k)
- This is also called direct proportion
If $y$ and $x^{n}$ (for positive integer n) vary directly then:
- It is denoted as $y \propto x^{n}$
- $y = k x^{n}$ for some constant k
  - This can be written as $\frac{y}{x^{n}} = k$
The graphs of these models always start at the origin

How do I solve direct variation problems?

Identify which two variables vary directly
- It might not be $x$ and $y$
- It could be $x^{3}$ and $y$
Use the given information to find their constant ratio k
- Also called constant of proportionality
- Substitute the given values of $x$ and $y$ into your formula
- Solve to find k
Write the equation which models their relationship
- $y = k x^{n}$
You can then use the equation to solve problems

Worked example

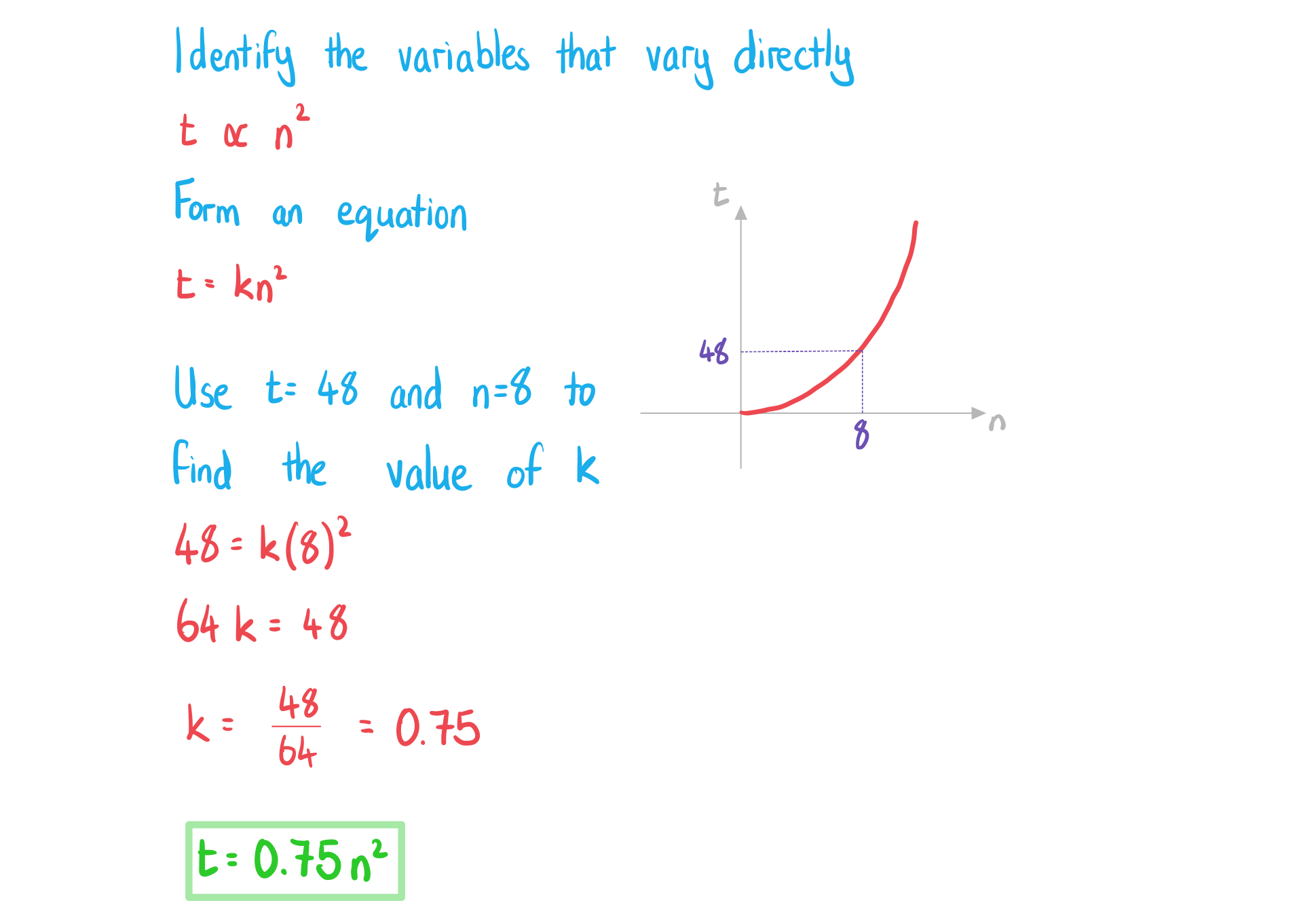
A computer program sorts a list of numbers into ascending order. The time it takes, $t$ milliseconds, varies directly with the square of the number of items, $n$ , in the list. The computer program takes 48 milliseconds to order a list with 8 items.

Find an equation connecting

t

and

n

2-3-4-ib-ai-sl-direct-variation-a-we-solution

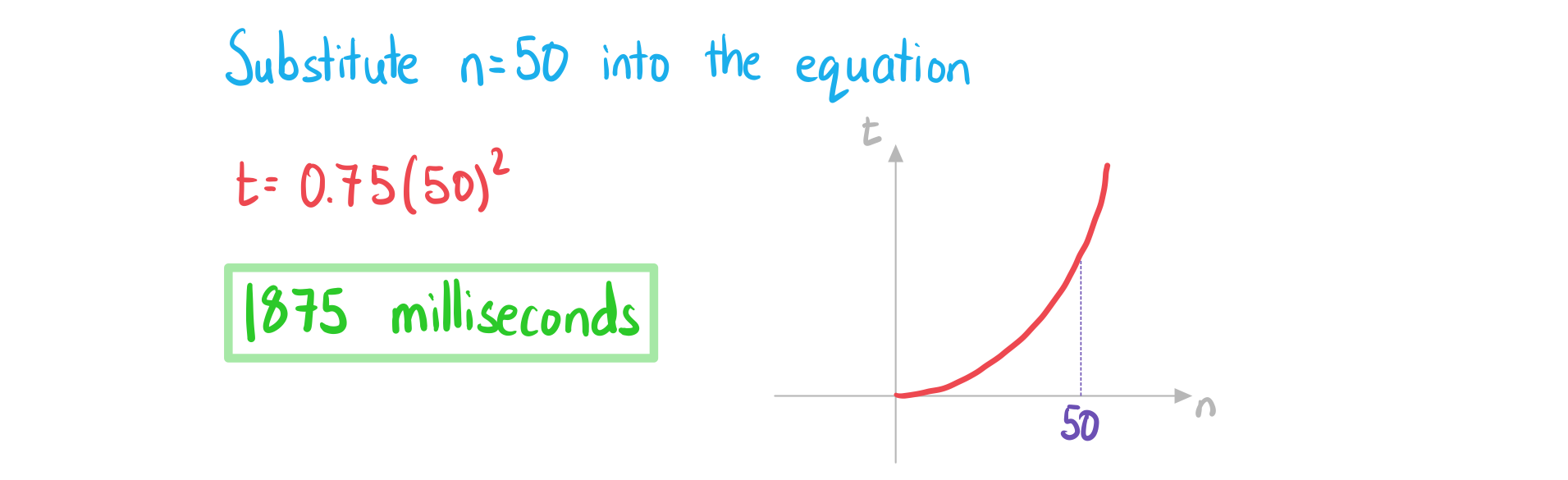
Find the time it takes to order a list of 50 numbers.

2-3-4-ib-ai-sl-direct-variation-b-we-solution

Did this video help you?

Inverse Variation

What is inverse variation?

Two variables are said to vary inversely if their product is constant (k)
- This is also called inverse proportion
If $y$ and $x^{n}$ (for positive integer n) vary inversely then:
- It is denoted $y \propto \frac{1}{x^{n}}$
- $y = \frac{k}{x^{n}}$ for some constant k
  - This can be written $x^{n} y = k$
The graphs of these models all have a vertical asymptote at the y-axis
- This means that as $x$ gets closer to 0 the absolute value of $y$ gets further away from 0
- $x$ can never equal 0

How do I solve inverse variation problems?

Identify which two variables vary inversely
- It might not be $x$ and $y$
- It could be $x^{3}$ and $y$
Use the given information to find their constant product k
- Also called constant of proportionality
- Substitute the given values of $x$ and $y$ into your formula
- Solve to find k
Write the equation which models their relationship
- $y = \frac{k}{x^{n}}$
You can then use the equation to solve problems

Examiner Tip

Reciprocal graphs generally have two parts/curves
- Only one – usually the positive – may be relevant to the model
- Think about why x/t/θ can only take positive values - refer to the context of the question

Worked example

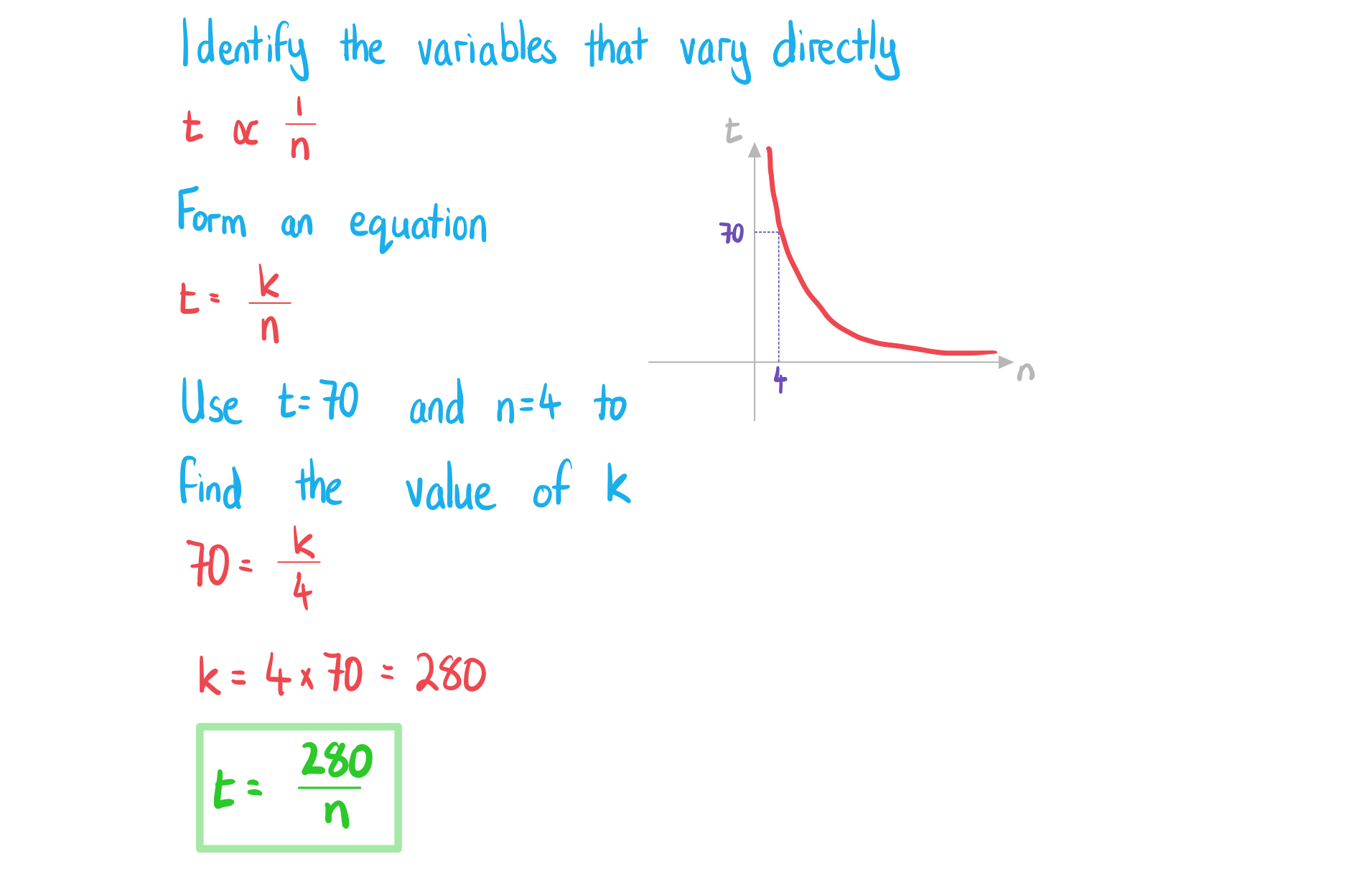
The time, $t$ hours, it takes to complete a project varies inversely to the number of people working on it, $n$ . If 4 people work on the project it takes 70 hours to complete.

Write an equation connecting

t

and

n

2-3-4-ib-ai-sl-inverse-variation-a-we-solution

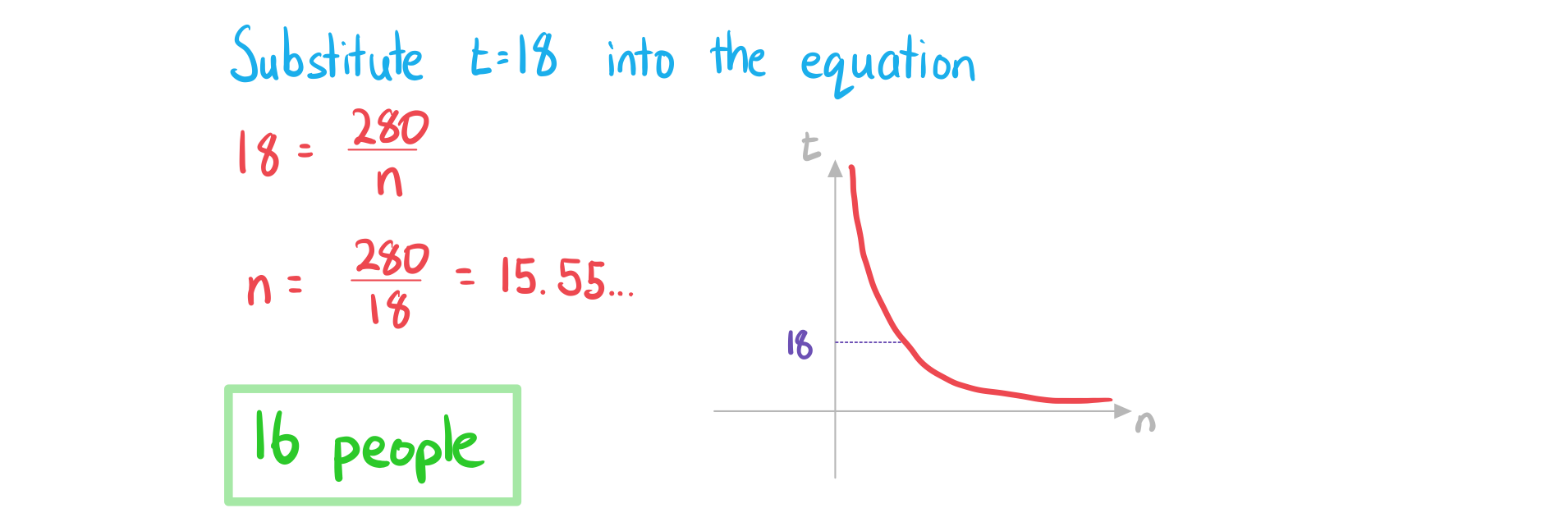
Given that the project needs to be completed within 18 hours, find the minimum number of people needed to work on it.

2-3-4-ib-ai-sl-inverse-variation-b-we-solution

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself Flashcards Next topic

Did this page help you?