Revision NotesExam QuestionsFlashcards
IBMaths: AI HLDPRevision Notes2. Functions2.3 Modelling with Functions2.3.3 Exponential Models

Exponential Models (DP IB Maths: AI HL)

Revision Note

Dan

Author

Dan

Last updated

Did this video help you?

Exponential Models

What are the parameters of an exponential model?

  • An exponential model is of the form
    •  space f left parenthesis x right parenthesis equals k a to the power of x plus c or space f left parenthesis x right parenthesis equals k a to the power of negative x end exponent plus c for space a greater than 0
    • space f open parentheses x close parentheses equals k straight e to the power of r x end exponent plus c
      • Where e is the mathematical constant 2.718…
    • The c represents the boundary for the function
      • It can never be this value
    • The a or r describes the rate of growth or decay
      • The bigger the value of a or the absolute value of r the faster the function increases/decreases

What can be modelled as an exponential model?

  • Exponential growth or decay
    • Exponential growth is represented by
      • a to the power of x where a greater than 1
      • a to the power of negative x end exponent where 0 less than a less than 1
      • straight e to the power of r x end exponent where r greater than 0
    • Exponential decay is represented by
      • a to the power of x where 0 less than a less than 1
      • a to the power of negative x end exponent where a greater than 1 
      • straight e to the power of r x end exponent where r less than 0
  • They can be used when there a constant percentage increase or decrease
    • Such as functions generated by geometric sequences
  • Examples include:
    • V(t) is the value of car after t years
    • S(t) is the amount in a savings account after t years
    • B(t) is the amount of bacteria on a surface after t seconds
    • T(t) is the temperature of a kettle t minutes after being boiled

What are possible limitations of an exponential model?

  • An exponential growth model does not have a maximum
    • In real-life this might not be the case
    • The function might reach a maximum and stay at this value
  • Exponential models are monotonic
    • In real-life this might not be the case
    • The function might fluctuate

How can I find the half-life using an exponential model?

  • You may need to find the half-life of a substance
    • This is the time taken for the mass of a substance to halve
  • Given an exponential model space f open parentheses t close parentheses equals k a to the power of negative t end exponent or space f open parentheses t close parentheses equals k straight e to the power of negative r t end exponent the half-life is the value of t such that:
    • space f left parenthesis t right parenthesis equals k over 2
    • You can solve for t using your GDC
  • For space f open parentheses t close parentheses equals k a to the power of negative t end exponent the half-life is given by t equals fraction numerator ln 2 over denominator ln a end fraction
    • k over 2 equals k a to the power of negative t end exponent
    • a to the power of t equals 2
    • t space ln a equals ln 2
  • For space f open parentheses t close parentheses equals k straight e to the power of negative r t end exponent the half-life is given by t equals fraction numerator ln 2 over denominator r end fraction
    • k over 2 equals k straight e to the power of negative r t end exponent
    • straight e to the power of r t end exponent equals 2
    • r t equals ln 2

Examiner Tip

  • Look out for the word "initial" or similar, as a way of asking you to make the power equal to zero to simplify the equation
  • Questions regarding the boundary of the exponential model are also frequently asked

Worked example

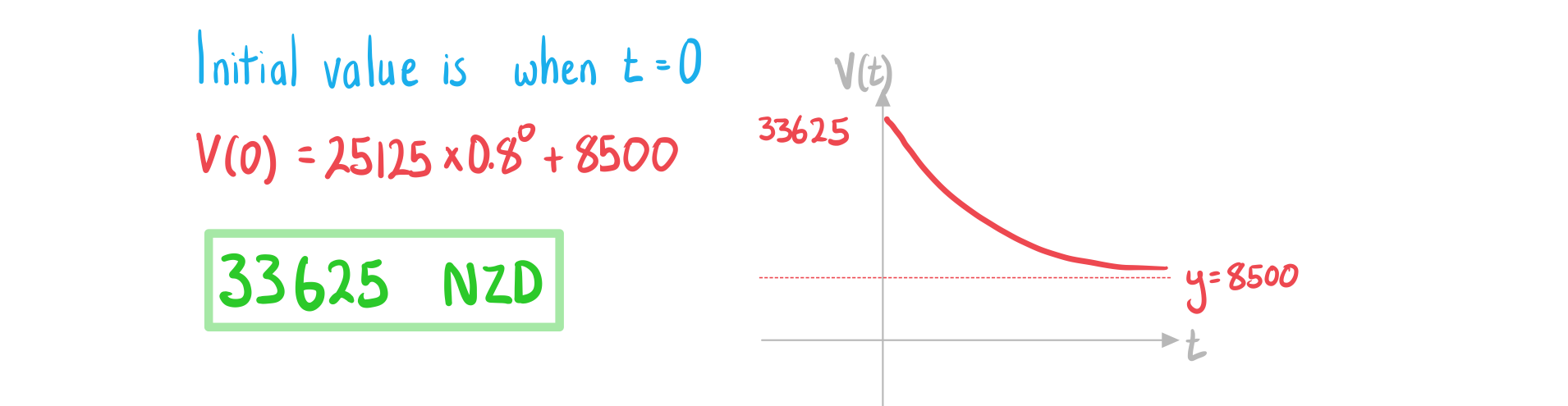
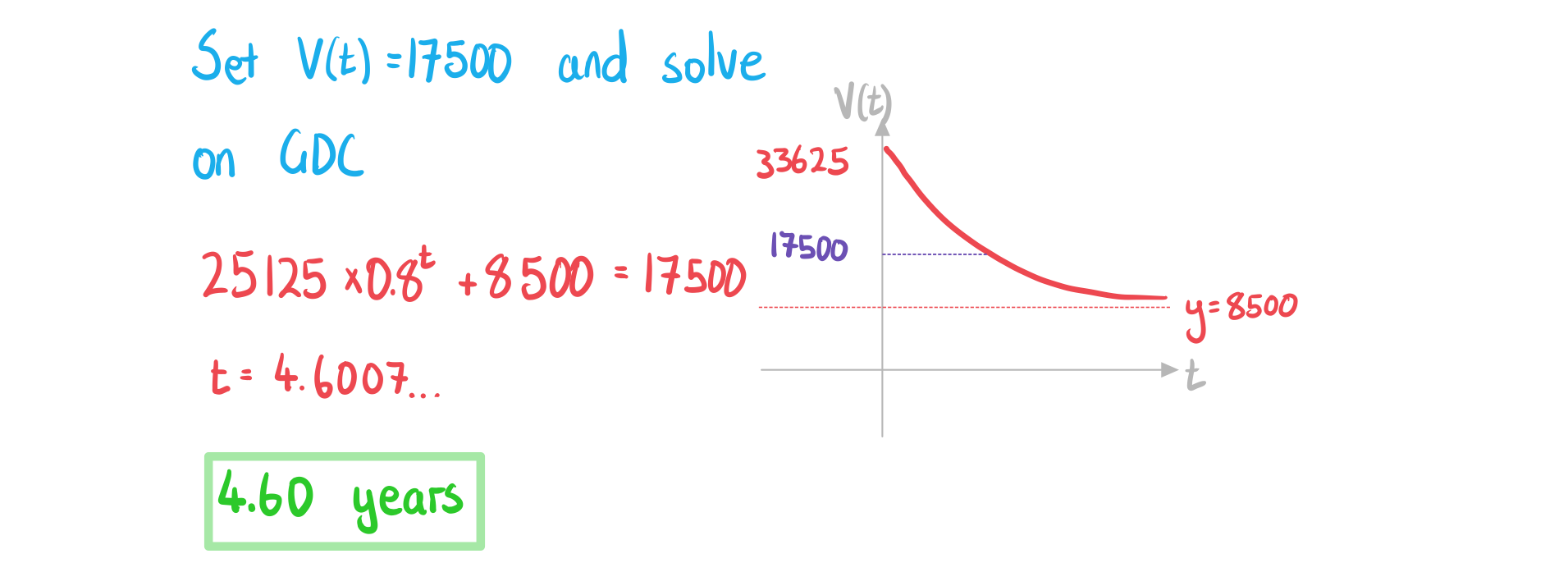
The value of a car, V (NZD), can be modelled by the function

space V open parentheses t close parentheses equals 25125 cross times 0.8 to the power of t plus 8500 comma blank t greater or equal than 0

where t is the age of the car in years.

a)
State the initial value of the car.

2-3-3-ib-ai-sl-exponential-models-a-we-solution

b)
Find the age of the car when its value is 17500 NZD.

2-3-3-ib-ai-sl-exponential-models-b-we-solution

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards

    Did this page help you?

    Previous:2.3.2 Quadratic & Cubic ModelsNext:2.3.4 Direct & Inverse Variation
    Dan

    Author: Dan

    Expertise: Maths

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.