IBMaths: AI HLDPRevision Notes2. Functions2.2 Further Functions & Graphs2.2.3 Properties of Graphs

Properties of Graphs (DP IB Maths: AI HL)

Revision Note

Test yourselfFlashcards
Dan

Author

Dan

Last updated

Did this video help you?

Quadratic Functions & Graphs

What are the key features of quadratic graphs?

  • A quadratic graph is of the form space y equals a x squared plus b x plus c where space a not equal to 0.
  • The value of a affects the shape of the curve
    • If a is positive the shape is union
    • If a is negative the shape is intersection
  • The y-intercept is at the point (0, c)
  • The zeros or roots are the solutions to space a x squared plus b x plus c equals 0
    • These can be found using your GDC or the quadratic formula
    • These are also called the x-intercepts
    • There can be 0, 1 or 2 x-intercepts
  • There is an axis of symmetry at space x equals negative fraction numerator b over denominator 2 a end fraction
    • This is given in your formula booklet
    • If there are two x-intercepts then the axis of symmetry goes through the midpoint of them
  • The vertex lies on the axis of symmetry
    • The x-coordinate is space minus fraction numerator b over denominator 2 a end fraction
    • The y-coordinate can be found using the GDC or by calculating y when space x equals negative fraction numerator b over denominator 2 a end fraction
    • If a is positive then the vertex is the minimum point
    • If a is negative then the vertex is the maximum point

Quadratic Graphs Notes Diagram 1Quadratic Graphs Notes Diagram 2

Examiner Tip

  • Use your GDC to find the roots and the turning point of a quadratic function
    • You do not need to factorise or complete the square
    • It is good exam technique to sketch the graph from your GDC as part of your working

Worked example

a)
Write down the equation of the axis of symmetry for the graph space y equals 4 x squared minus 4 x minus 3.

2-2-3-ib-ai-sl-quad--cub-graphs-a-we-solution

b)
Sketch the graph space y equals 4 x squared minus 4 x minus 3.

2-2-3-ib-ai-sl-quad--cub-graphs-b-we-solution

Did this video help you?

Cubic Functions & Graphs

What are the key features of cubic graphs?

  • A cubic graph is of the form space y equals a x cubed plus b x squared plus c x plus d where space a not equal to 0.
  • The value of a affects the shape of the curve
    • If a is positive the graph goes from bottom left to top right
    • If a is negative the graph goes from top left to bottom right
  • The y-intercept is at the point (0, d)
  • The zeros or roots are the solutions to space a x cubed plus b x squared plus c x plus d equals 0
    • These can be found using your GDC
    • These are also called the x-intercepts
    • There can be 1, 2 or 3 x-intercepts
      • There is always at least 1
  • There are either 0 or 2 local minimums/maximums
    • If there are 0 then the curve is monotonic (always increasing or always decreasing)
    • If there are 2 then one is a local minimum and one is a local maximum

Sketching Polynomials Notes Diagram 1

Examiner Tip

  • Use your GDC to find the roots, the local maximum and local minimum of a cubic function
  • When drawing/sketching the graph of a cubic function be sure to label all the key features
    • x and y axes intercepts
    • the local maximum point
    • the local minimum point

Worked example

Sketch the graph space y equals 2 x cubed minus 6 x squared plus x minus 3.

2-2-3-ib-ai-sl-quad--cub-graphs-c-we-solution

Did this video help you?

Exponential Functions & Graphs

What are the key features of exponential graphs?

  • An exponential graph is of the form
    • space y equals k a to the power of x plus c or space y equals k a to the power of negative x end exponent plus c where space a greater than 0
    • space y equals k straight e to the power of r x end exponent plus c
      • Where e is the mathematical constant 2.718…
  • The y-intercept is at the point (0, k + c)
  • There is a horizontal asymptote at y = c
  • The value of k determines whether the graph is above or below the asymptote
    • If k is positive the graph is  above the asymptote
      • So the range is space y greater than c
    • If k is negative the graph is below the asymptote
      • So the range is space y less than c
  • The coefficient of x and the constant k determine whether the graph is increasing or decreasing
    • If the coefficient of x and k have the same sign then graph is increasing
    • If the coefficient of x and k have different signs then the graph is decreasing
  • There is at most 1 root
    • It can be found using your GDC

exponential-graphs

Examiner Tip

  • You may have to change the viewing window settings on your GDC to make asymptotes clear
    • A small scale can make it look as though the curve and an asymptote intercept
  • Be careful about how two exponential graphs drawn on the same axes look
    • Particularly which one is "on top" either side of the y-axis

Worked example

a)
On the same set of axes sketch the graphs space y equals 2 to the power of x and space y equals 3 to the power of x. Clearly label each graph.

2-2-3-ib-ai-sl-exp-graphs-a-we-solution

b)
Sketch the graph space y equals 2 straight e to the power of negative 3 x end exponent plus 1.

2-2-3-ib-ai-sl-exp-graphs-b-we-solution

Did this video help you?

Sinusoidal Functions & Graphs

What are the key features of sinusoidal graphs?

  • A sinusoidal graph is of the form
    • space y equals a sin left parenthesis b open parentheses x minus c close parentheses right parenthesis plus d
    • space y equals a cos left parenthesis b open parentheses x minus c close parentheses right parenthesis plus d
  • The y-intercept is at the point where x = 0
    • (0, -asin(bc) + d) for space y equals a sin left parenthesis b open parentheses x minus c close parentheses right parenthesis plus d
    • (0, acos(bc) + d) for space y equals a cos left parenthesis b open parentheses x minus c close parentheses right parenthesis plus d
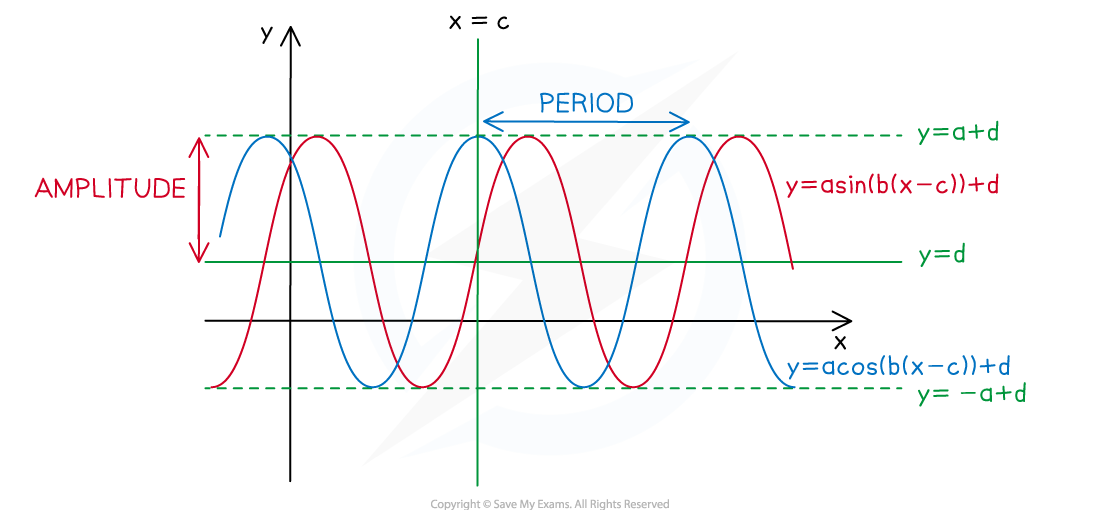
  • The period of the graph is the length of the interval of a full cycle
    • This is fraction numerator 360 degree over denominator b end fraction (in degrees) or fraction numerator 2 pi over denominator b end fraction
  • The maximum value is y = a + d
  • The minimum value is y = -a + d
  • The principal axis is the horizontal line halfway between the maximum and minimum values
    • This is y = d
  • The amplitude is the vertical distance from the principal axis to the maximum value
    • This is a
  • The phase shift is the horizontal distance from its usual position
    • This is c

ib-aa-sl-3-5-3-transformations-of-trig-graphs

Examiner Tip

  • Make sure your angle setting is in the correct mode (degrees or radians) at the start of a question involving sinusoidal functions
  • Pay careful attention to the angles between which you are required to use or draw/sketch a sinusoidal graph
    • e.g.  0° ≤ x ≤ 360°

Worked example

a)
Sketch the graph space y equals 3 sin left parenthesis 2 open parentheses x degree minus 15 degree close parentheses right parenthesis plus 1 for the values space 0 less or equal than x less or equal than 360.

2-2-3-ib-ai-hl-sinusoidal-graphs-a-we-solution

b)
State the equation of the principal axis of the curve.

2-2-3-ib-ai-sl-sinusoidal-graphs-b-we-solution

c)
State the period and amplitude.

2-2-3-ib-ai-sl-sinusoidal-graphs-c-we-solution

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcardsNext topic

    Did this page help you?

    Dan

    Author: Dan

    Expertise: Maths

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.