Introduction to Matrices (DP IB Maths: AI HL): Revision Note

Matrices are a useful way to represent and manipulate data in order to model situations. The elements in a matrix can represent data, equations or systems and have many real-life applications.

What are matrices?

• A matrix is a rectangular array of elements (numerical or algebraic) that are arranged in rows and columns
• The order of a matrix is defined by the number of rows and columns that it has
  • The order of a matrix with  rows and columns is 
• A matrix  can be defined by  where and and refers to the element in row , column 

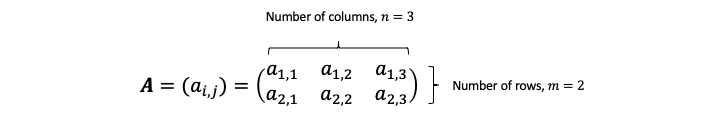
What type of matrices are there?

• A column matrix (or column vector) is a matrix with a single column, 
• A row matrix is a matrix with a single row, 
• A square matrix is one in which the number of rows is equal to the number of columns, 
• Two matrices are equal when they are of the same order and their corresponding elements are equal, i.e. for all elements
• A zero matrix, , is a matrix in which all the elements are , e.g. 
• The identity matrix, , is a square matrix in which all elements along the leading diagonal are  and the rest are , e.g.