Did this video help you?
Compound Interest & Depreciation (DP IB Maths: AI HL): Revision Note
Compound Interest
What is compound interest?
- Interest is a small percentage paid by a bank or company that is added on to an initial investment
- Interest can also refer to an amount paid on a loan or debt, however IB compound interest questions will always refer to interest on investments
- Compound interest is where interest is paid on both the initial investment and any interest that has already been paid
- Make sure you know the difference between compound interest and simple interest
- Simple interest pays interest only on the initial investment
- Make sure you know the difference between compound interest and simple interest
- The interest paid each time will increase as it is a percentage of a higher number
- Compound interest will be paid in instalments in a given timeframe
- The interest rate, r, will be per annum (per year)
- This could be written r % p.a.
- Look out for phrases such as compounding annually (interest paid yearly) or compounding monthly (interest paid monthly)
- If
p.a. (per annum) is paid compounding monthly, then
will be paid each month
- The formula for compound interest allows for this so you do not have to compensate separately
- If
- The interest rate, r, will be per annum (per year)
How is compound interest calculated?
- The formula for calculating compound interest is:
-
- Where
- FV is the future value
- PV is the present value
- n is the number of years
- k is the number of compounding periods per year
- r % is the nominal annual rate of interest
- This formula is given in the formula booklet, you do not have to remember it
- Where
- Be careful with the k value
- Compounding annually means k = 1
- Compounding half-yearly means k = 2
- Compounding quarterly means k = 4
- Compounding monthly means k = 12
- Your GDC will have a finance solver app on it which you can use to find the future value
- This may also be called the TVM (time value of money) solver
- You will have to enter the information from the question into your calculator
- Be aware that many questions will be set up such that you will have to use the formula
- So for compound interest questions it is better to use the formula from your formula booklet than your GDC
Examiner Tip
- Your GDC will be able to solve some compound interest problems so it is a good idea to make sure you are confident using it, however you must also familiarise yourself with the formula and make sure you can find it in the formula booklet
Worked example
Kim invests MYR 2000 (Malaysian Ringgit) in an account that pays a nominal annual interest rate of 2.5% compounded monthly. Calculate the amount that Kim will have in her account after 5 years.

Did this video help you?
Depreciation
What is depreciation?
- Depreciation is when the value of something falls over time
- The most common examples of depreciation are the value of cars and technology
- If the depreciation is occurring at a constant rate then it is compound depreciation
How is compound depreciation calculated?
- The formula for calculating compound depreciation is:
-
- Where
- FV is the future value
- PV is the present value
- n is the number of years
- r% is the rate of depreciation
- This formula is not given in the formula booklet, however it is almost the same as the formula for compound interest but
- with a subtraction instead of an addition
- the value of k will always be 1
- Where
- Your GDC could again be used to solve some compound depreciation questions, but watch out for those which are set up such that you will have to use the formula
Examiner Tip
- You can use your GDC's "Finance Solver" (TI) or "Compound Interest" (Casio) feature to solve most depreciation questions, by entering the interest rate as a negative value
Worked example
Kyle buys a new car for AUD $14 999. The value of the car depreciates by 15% each year.
a)
Find the value of the car after 5 years.

b)
Find the number of years and months it will take for the value of the car to be approximately AUD $9999.
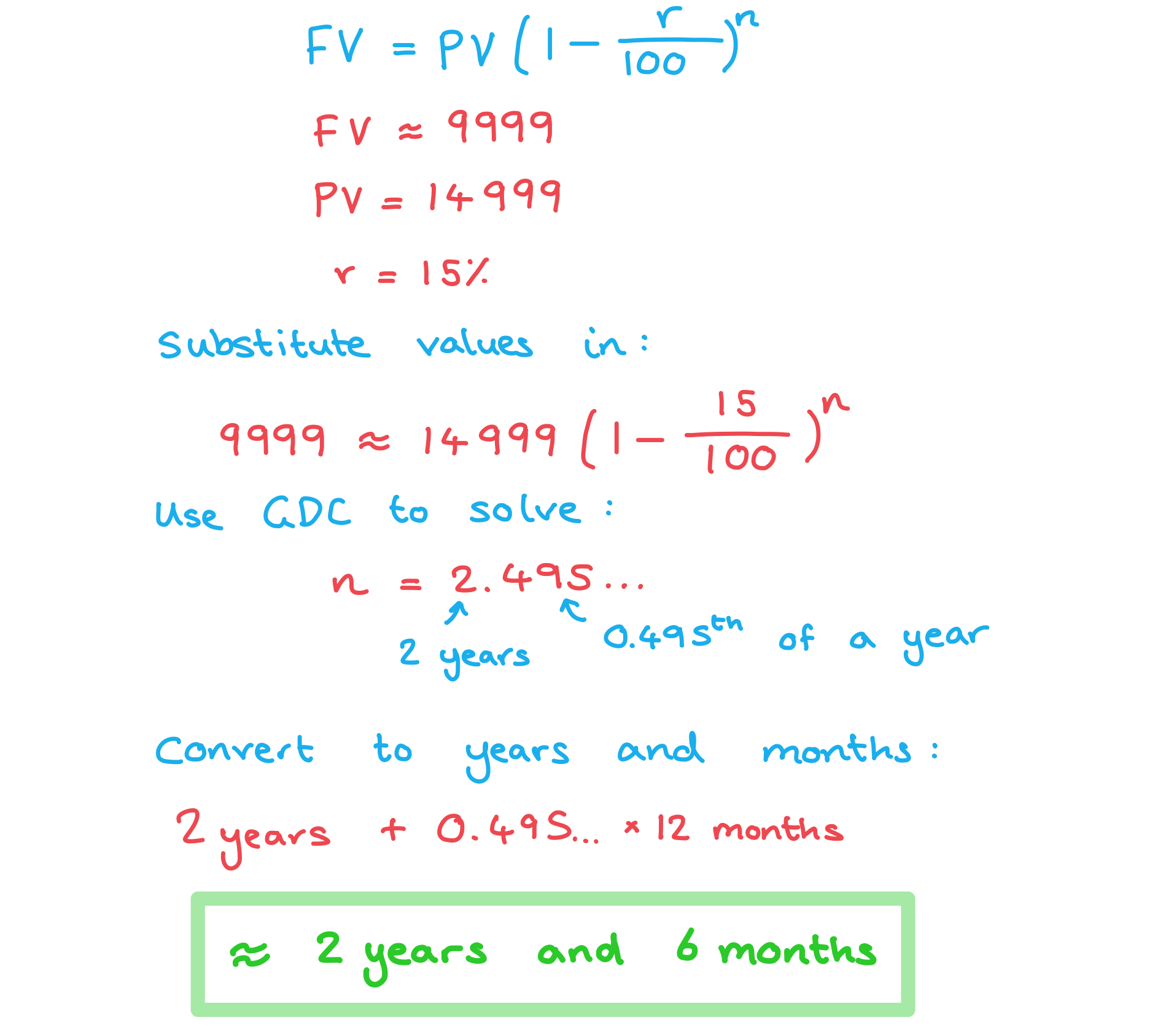

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
