Logarithms (DP IB Applications & Interpretation (AI)) : Revision Note
Did this video help you?
Introduction to Logarithms
What are logarithms?
A logarithm is the inverse of an exponent
If
then
where a > 0, b > 0, a ≠ 1
This is in the formula booklet
The number a is called the base of the logarithm
Your GDC will be able to use this function to solve equations involving exponents
Try to get used to ‘reading’ logarithm statements to yourself
would be read as “the power that you raise
to, to get
, is
”
So
would be read as “the power that you raise 5 to, to get 125, is 3”
Two important cases are:
Where e is the mathematical constant 2.718…
This is called the natural logarithm and will have its own button on your GDC
Logarithms of base 10 are used often and so abbreviated to log x
Why use logarithms?
Logarithms allow us to solve equations where the exponent is the unknown value
We can solve some of these by inspection
For example, for the equation 2x = 8 we know that x must be 3
Logarithms allow use to solve more complicated problems
For example, the equation 2x = 10 does not have a clear answer
Instead, we can use our GDCs to find the value of
Examiner Tips and Tricks
Before going into the exam, make sure you are completely familiar with your GDC and know how to use its logarithm functions
Worked Example
Solve the following equations:
i) ,

ii) , giving your answer to 3 s.f.

Did this video help you?
Laws of Logarithms
What are the laws of logarithms?
Laws of logarithms allow you to simplify and manipulate expressions involving logarithms
The laws of logarithms are equivalent to the laws of indices
The laws you need to know are, given
:
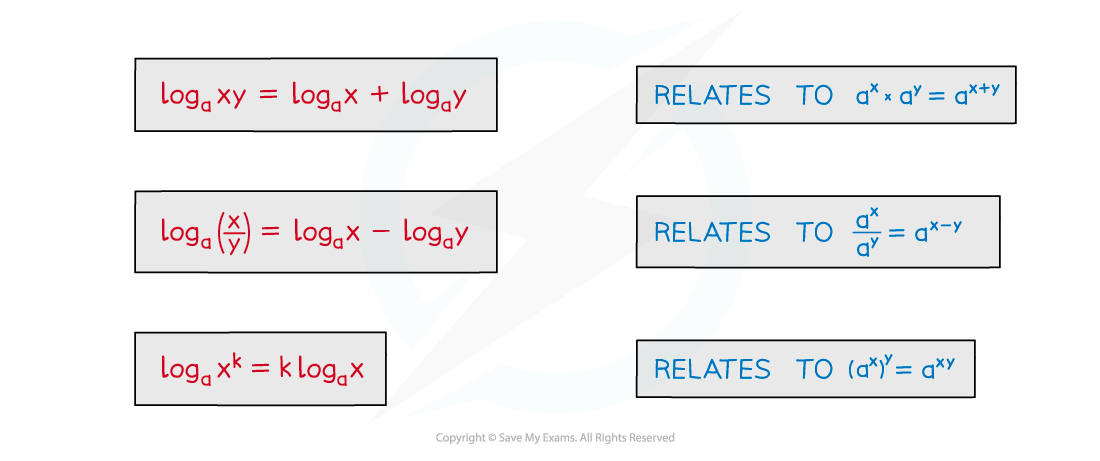
This relates to
This relates to
This relates to
These laws are in the formula booklet so you do not need to remember them
You must make sure you know how to use them
Useful results from the laws of logarithms
Given
This is equivalent to
If we substitute b for a into the given identity in the formula booklet
where
gives
This is an important and useful result
Substituting this into the third law gives the result
Taking the inverse of its operation gives the result
From the third law we can also conclude that
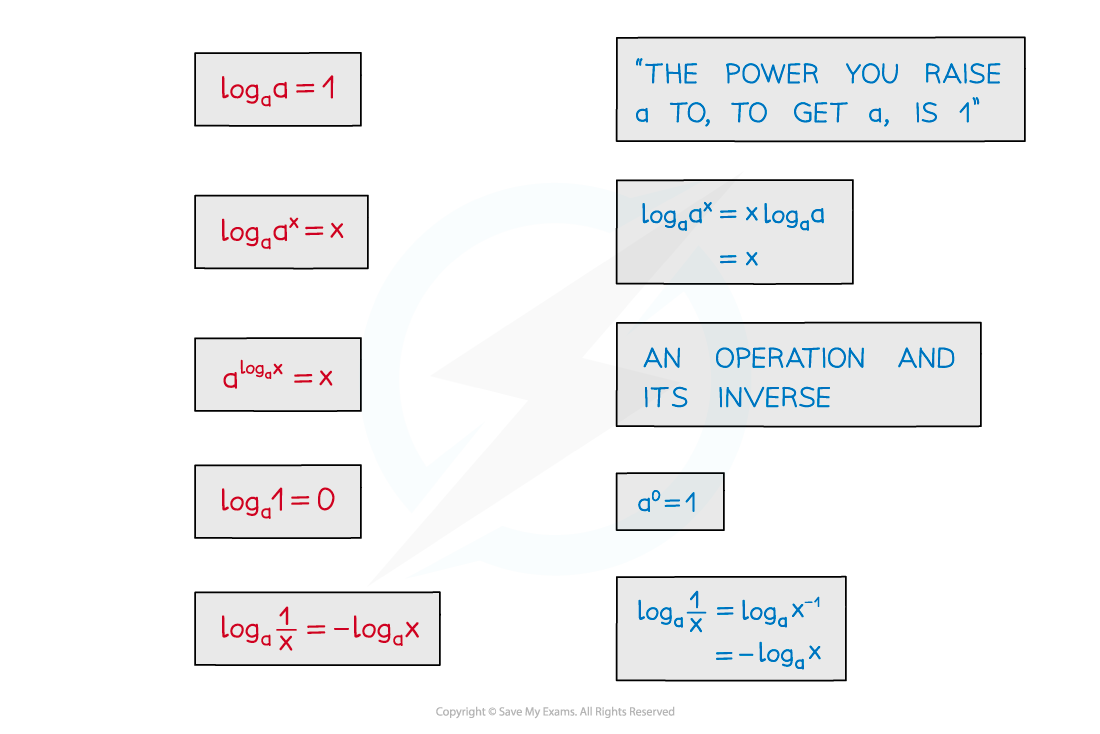
These useful results are not in the formula booklet but can be deduced from the laws that are
Beware…
…
These results apply to
too
Two particularly useful results are
Laws of logarithms can be used to …
simplify expressions
solve logarithmic equations
solve exponential equations
Examiner Tips and Tricks
Remember to check whether your solutions are valid
log (x+k) is only defined if x > -k
You will lose marks if you forget to reject invalid solutions
Worked Example
a) Write the expression in the form
, where
.
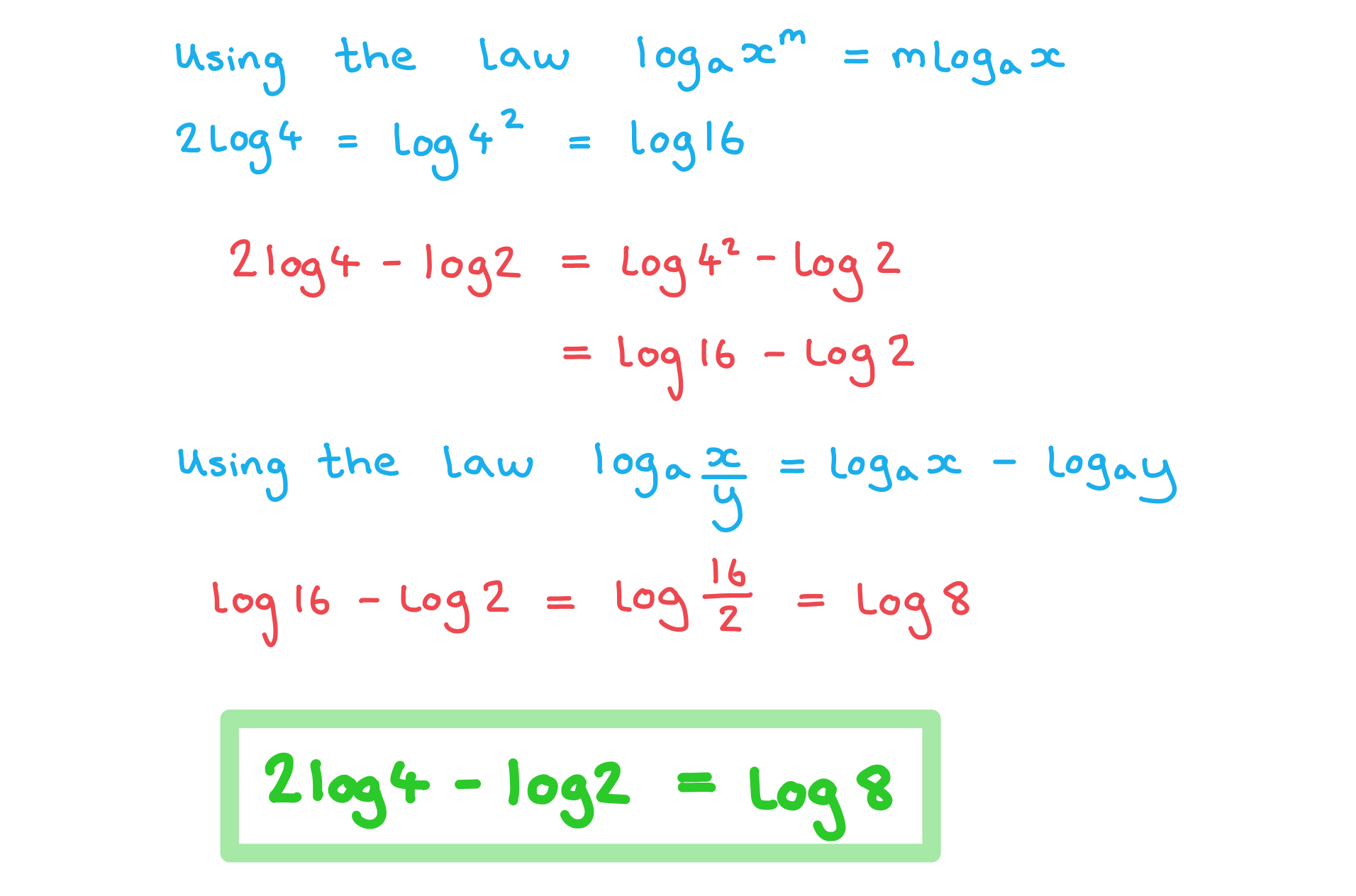
b) Hence, or otherwise, solve .
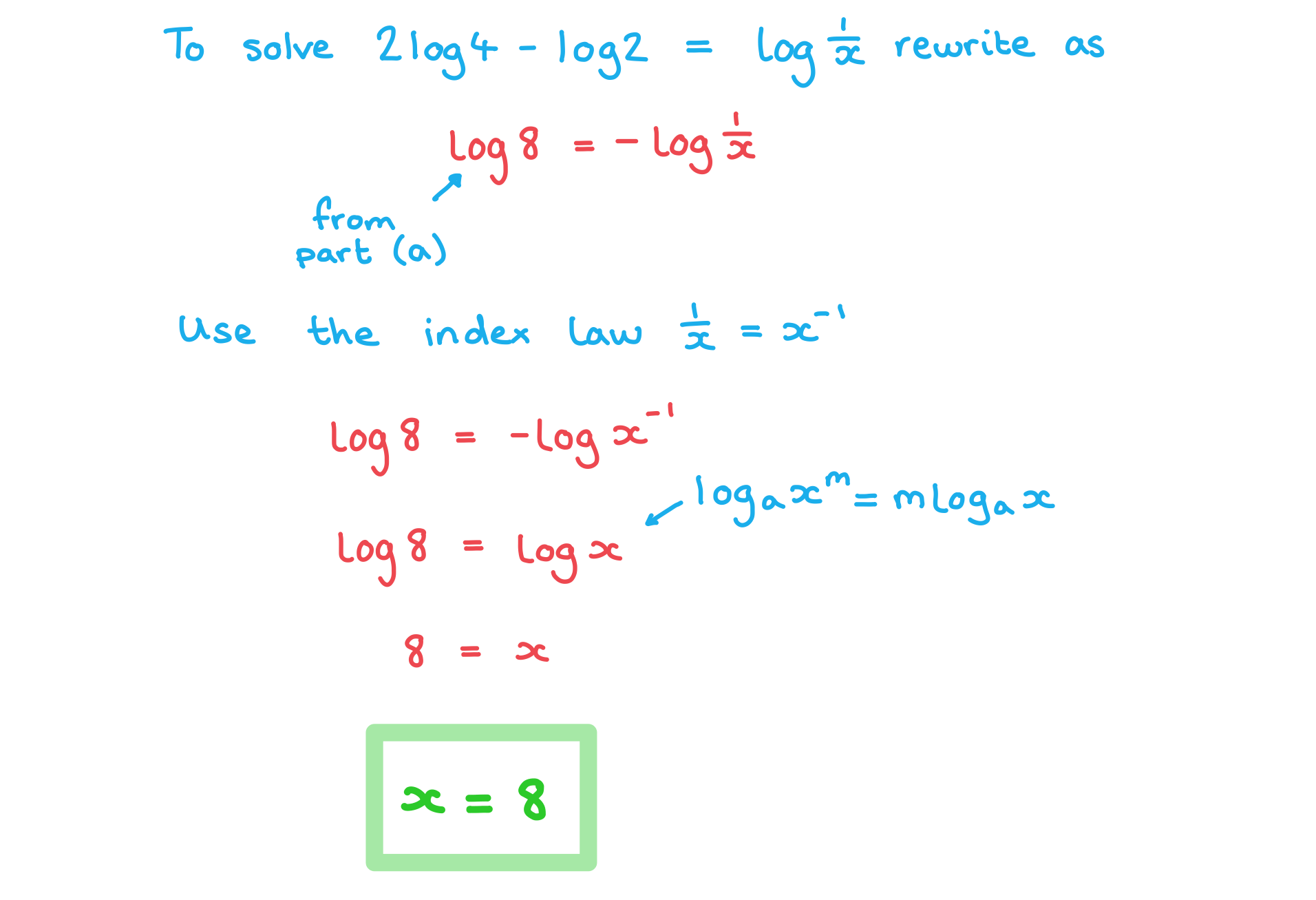

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
