The graph below shows the curve with equation in the interval
.
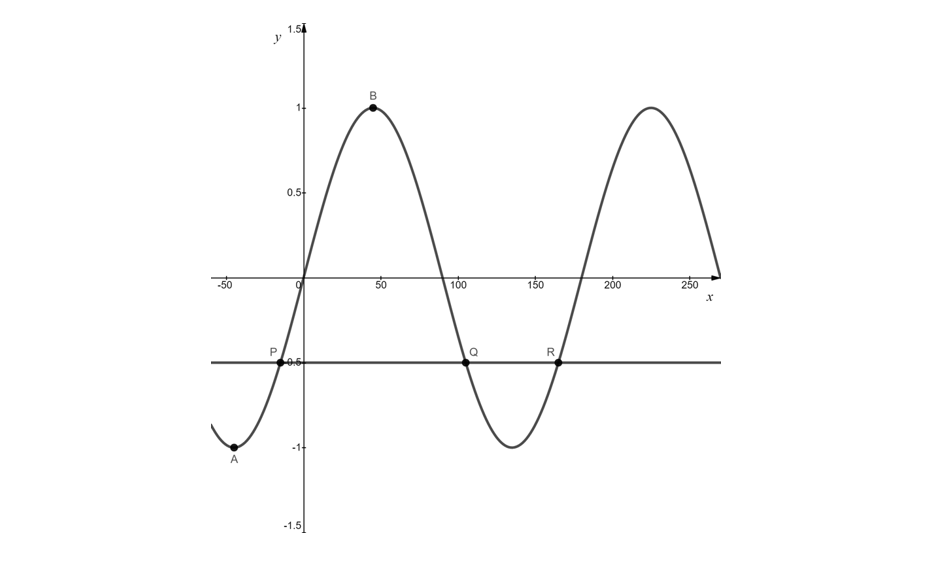
Point A has coordinates and is the minimum point closest to the origin. Point B is the maximum point closest to the origin. State the coordinates of B.
A straight line with equation meets the graph of
at the three points P, Q and R, as shown in the diagram.
Given that point P has coordinates , use graph symmetries to determine the coordinates of Q and R.
Did this page help you?





