Did this video help you?
Definite Integrals (DP IB Maths: AA SL): Revision Note
Definite Integrals
What is a definite integral?
- This is known as the Fundamental Theorem of Calculus
- a and b are called limits
- a is the lower limit
- b is the upper limit
is the integrand
is an antiderivative of
- The constant of integration (“+c”) is not needed in definite integration
- “+c” would appear alongside both F(a) and F(b)
- subtracting means the “+c”’s cancel
How do I find definite integrals analytically (manually)?
STEP 1
Give the integral a name to save having to rewrite the whole integral every time
If need be, rewrite the integral into an integrable form
STEP 2
Integrate without applying the limits; you will not need “+c”
Notation: use square brackets [ ] with limits placed at the end bracket
Notation: use square brackets [ ] with limits placed at the end bracket
STEP 3
Substitute the limits into the function and evaluate
Examiner Tip
- If a question does not state that you can use your GDC then you must show all of your working clearly, however it is always good practice to check you answer by using your GDC if you have it in the exam
Worked example
a)
Show that
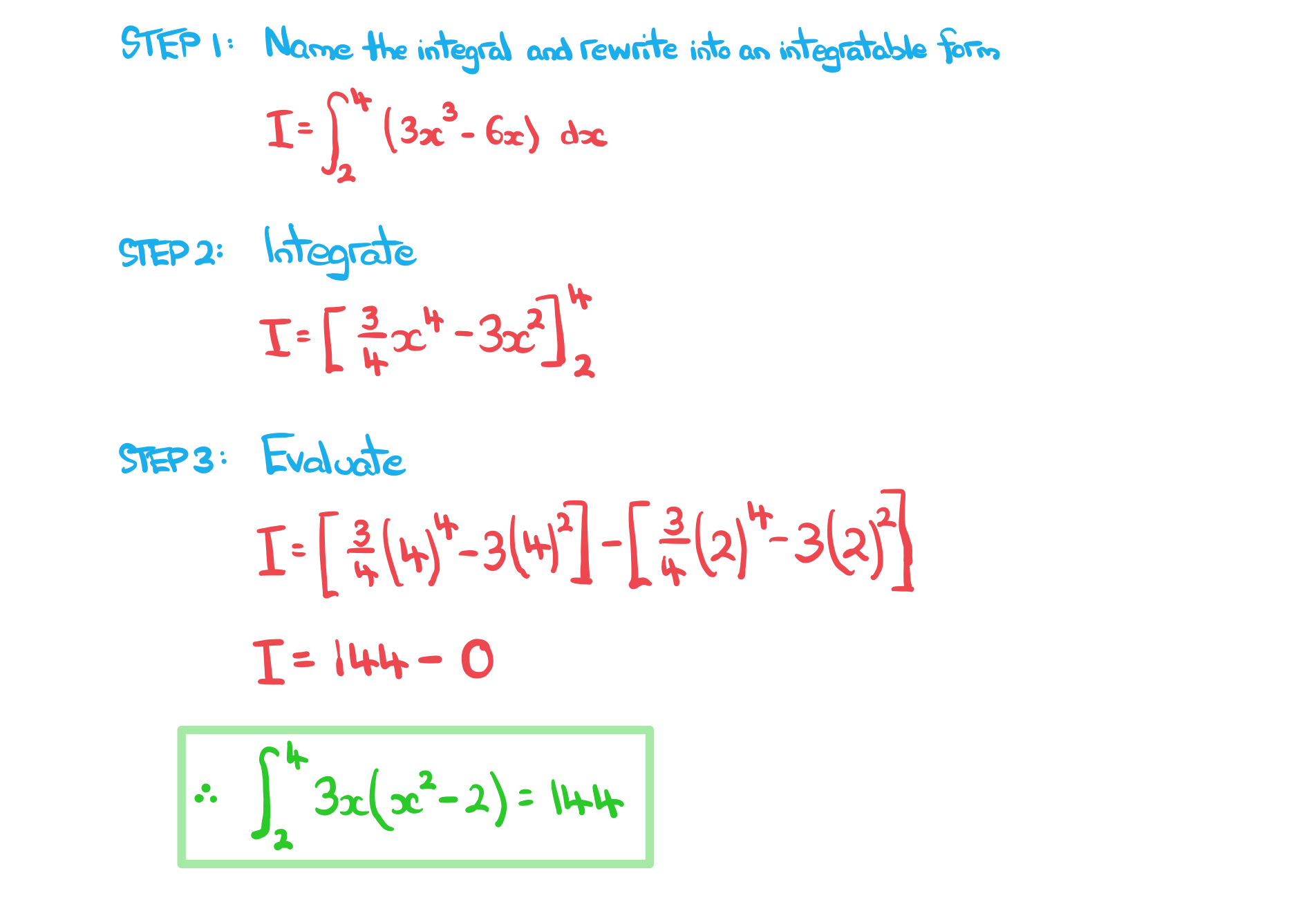
b)
Use your GDC to evaluate
giving your answer to three significant figures.

Did this video help you?
Properties of Definite Integrals
Fundamental Theorem of Calculus
- Formally,
is continuous in the interval
is an antiderivative of
What are the properties of definite integrals?
- Some of these have been encountered already and some may seem obvious …
- taking constant factors outside the integral
-
where
is a constant
- useful when fractional and/or negative values involved
-
- integrating term by term
- the above works for subtraction of terms/functions too
- equal upper and lower limits
- on evaluating, this would be a value, subtract itself !
- swapping limits gives the same, but negative, result
- compare 8 subtract 5 say, with 5 subtract 8 …
- splitting the interval
-
where
- this is particularly useful for areas under multiple curves or areas under the
-axis
-
- horizontal translations
-
where
is a constant
- the graph of
is a horizontal translation of the graph of
(translates left,
translates right)
- The rule in reverse is
-
- taking constant factors outside the integral
Examiner Tip
- Learning the properties of definite integrals can help to save time in the exam
Worked example
is a continuous function in the interval
.
It is known that and that
.
a)
Write down the values of
i)
ii)

b)
Find the values of
i)
ii)


You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
