Concavity & Points of Inflection | DP IB Maths: AA SL Revision Notes 2021

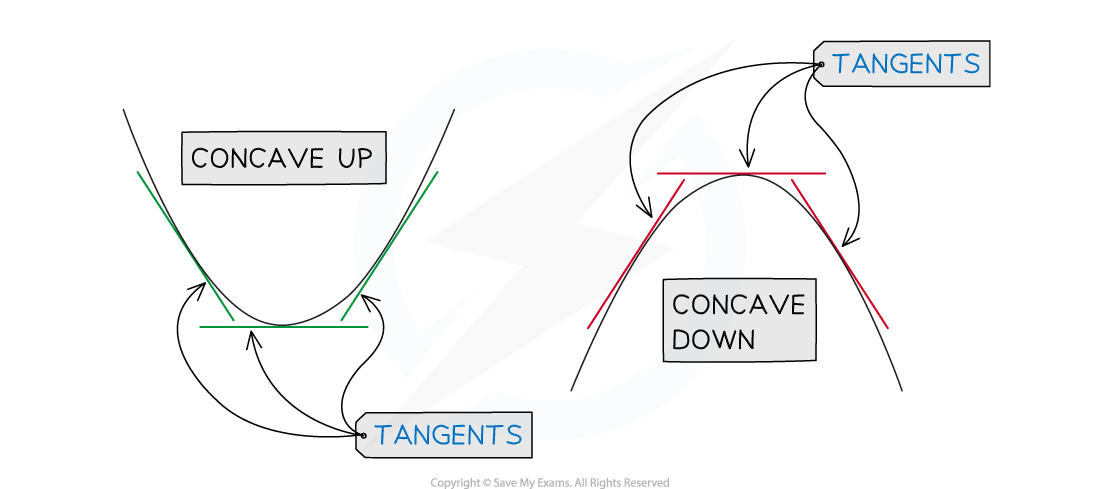
Concavity of a Function

What is concavity?

Concavity is the way in which a curve (or surface) bends
Mathematically,
- a curve is CONCAVE DOWN if $f'' (x) < 0$ for all values of $x$ in an interval
- a curve is CONCAVE UP if $f'' (x) > 0$ for all values of $x$ in an interval

Examiner Tip

In an exam an easy way to remember the difference is:
- Concave down is the shape of (the mouth of) a sad smiley ☹︎
- Concave up is the shape of (the mouth of) a happy smiley ☺︎

Worked example

The function $f (x)$ is given by $f (x) = x^{3} - 3 x + 2$ .

Determine whether the curve of the graph of

y = f (x)

is concave down or concave up at the points where

x = - 2

and

x = 2

5-2-5-ib-sl-aa-only-we1-soltn-a

Find the values of

x

for which the curve of the graph

y = f (x)

of is concave up.

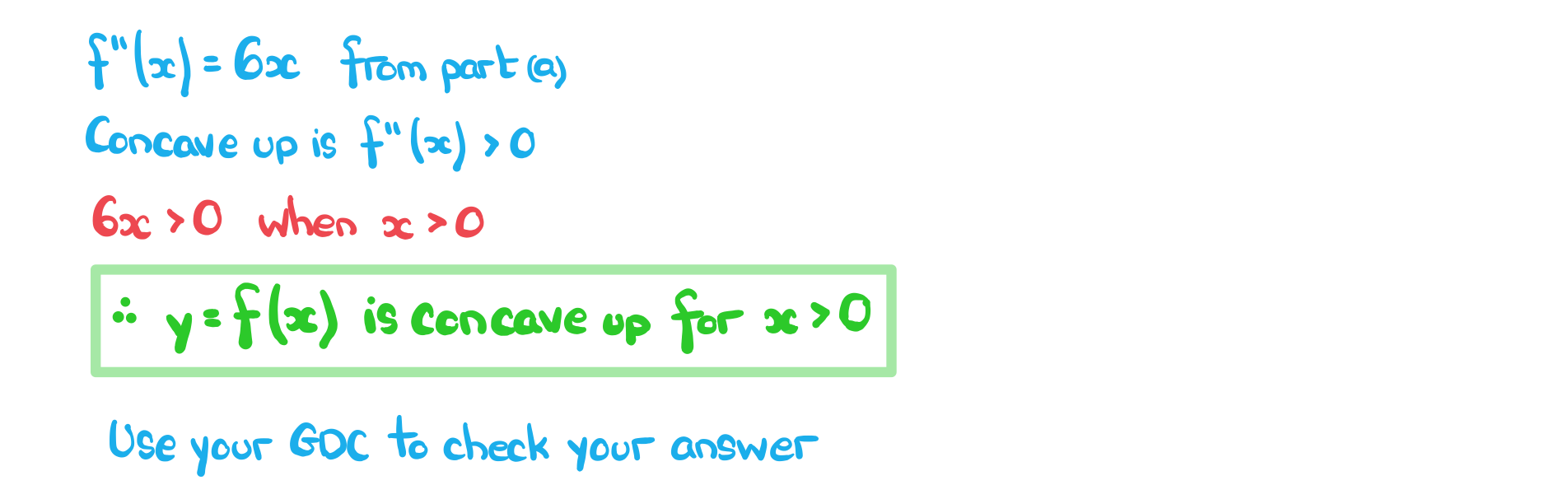
5-2-5-ib-sl-aa-only-we1-soltn-b

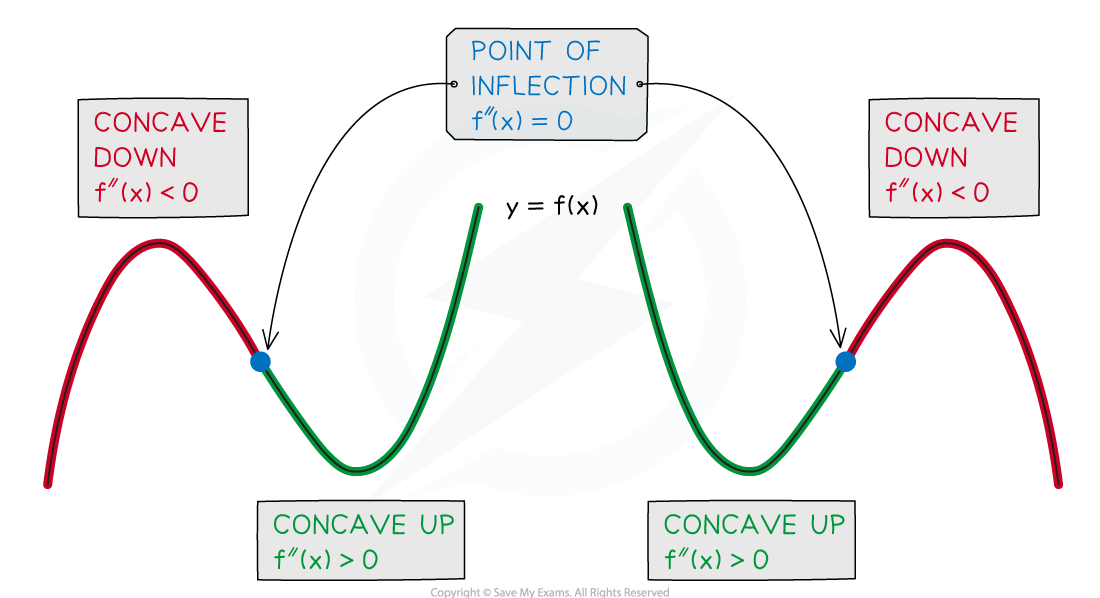
Points of Inflection

What is a point of inflection?

A point at which the curve of the graph of $y = f (x)$ changes concavity is a point of inflection
The alternative spelling, inflexion, may sometimes be used

What are the conditions for a point of inflection?

A point of inflection requires BOTH of the following two conditions to hold

- the second derivative is zero
  - $f'' (x) = 0$

AND

- the graph of $y = f (x)$ changes concavity
  - $f'' (x)$ changes sign through a point of inflection

It is important to understand that the first condition is not sufficient on its own to locate a point of inflection
- points where $f'' (x) = 0$ could be local minimum or maximum points
  - the first derivative test would be needed
- However, if it is already known $f (x)$ has a point of inflection at $x = a$ , say, then $f'' (a) = 0$

What about the first derivative, like with turning points?

A point of inflection, unlike a turning point, does not necessarily have to have a first derivative value of 0 ( $f' (x) = 0$ )
- If it does, it is also a stationary point and is often called a horizontal point of inflection
  - the tangent to the curve at this point would be horizontal
- The normal distribution is an example of a commonly used function that has a graph with two non-stationary points of inflection

How do I find the coordinates of a point of inflection?

For the function $f (x)$

STEP 1

Differentiate $f (x)$ twice to find $f'' (x)$ and solve $f'' (x) = 0$ to find the $x$ -coordinates of possible points of inflection

STEP 2

Use the second derivative to test the concavity of $f (x)$ either side of $x = a$

If $f'' (x) < 0$ then $f (x)$ is concave down
If $f'' (x) > 0$ then $f (x)$ is concave up

If concavity changes, $x = a$ is a point of inflection

STEP 3

If required, the $y$ -coordinate of a point of inflection can be found by substituting the $x$ -coordinate into $f (x)$

Examiner Tip

You can find the x-coordinates of the point of inflections of $y = f (x)$ by drawing the graph $y = f' (x)$ and finding the x-coordinates of any local maximum or local minimum points
Another way is to draw the graph $y = f'' (x)$ and find the x-coordinates of the points where the graph crosses (not just touches) the x-axis

Worked example

Find the coordinates of the point of inflection on the graph of $y = 2 x^{3} - 18 x^{2} + 24 x + 5$ .
Fully justify that your answer is a point of inflection.

5-2-5-ib-sl-aa-only-we2-soltn

Concavity & Points of Inflection (DP IB Maths: AA SL)

Revision Note

Concavity of a Function

Examiner Tip

Worked example

Points of Inflection

Examiner Tip

Worked example

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Paul