Revision NotesExam QuestionsFlashcardsPast PapersMock Exams
IBMathsDPAnalysis & Approaches (AA)SLRevision Notes3. Geometry & TrigonometryThe Unit Circle & Exact ValuesThe Unit Circle

The Unit Circle (DP IB Analysis & Approaches (AA)): Revision Note

Amber

Written by: Amber

Reviewed by: Dan Finlay

Updated on

DP Analysis & Approaches (AA): SLDP Analysis & Approaches (AA): HLDP Applications & Interpretation (AI): HL

Defining sin, cos and tan

What is the unit circle?

  • The unit circle is a circle with radius 1 and centre (0, 0)

  • Angles are always measured from the positive x-axis and turn:

    • anticlockwise for positive angles

    • clockwise for negative angles

How can the unit circle be used to define sin, cos and tan?

  • Measure the angle theta from the positive x-axis

  • Label the point on the circle open parentheses x comma space y close parentheses

  • The trigonometric ratios can be found using SOHCAHTOA

    • sin theta is the y-coordinate of the point

    • cos theta is the x-coordinate of the point

    • tan theta is the gradient of the line segment from the centre to the point

  • You can use these definitions to calculate sin, cos and tan for angles that are:

    • greater than 90°

    • negative

      • measure the angle clockwise

    • greater than 360°

      • go round the circle again

Diagram of a unit circle with radius 1 centred at (0,0), showing trigonometric concepts, angles in right triangles, and sine, cosine, tangent formulas.

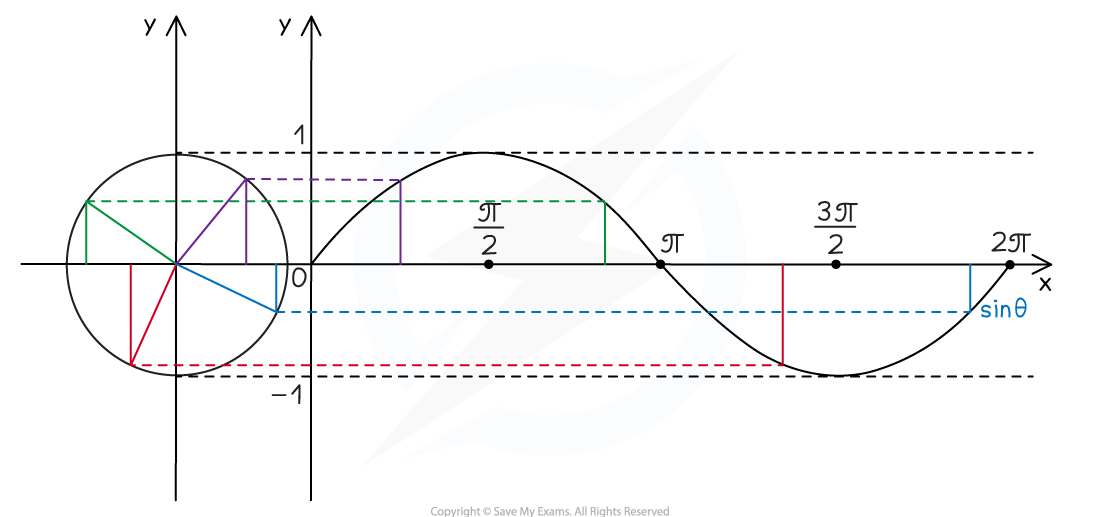
How can I use the unit circle to construct the sine graph?

  • The y-coordinates of the points on the unit circle give the values of sine

  • You can plot the y-coordinates against the angles to form the sine graph

  • You should remember the general shape

    • The sine graph starts at 0

    • It then increases and is equal to 1 when the angle is straight pi over 2

    • It then decreases and returns to 0 when the angle is straight pi

    • It continues to decrease and is equal to -1 when the angle is fraction numerator 3 straight pi over denominator 2 end fraction

    • It then increases and returns to 0 when the angle is 2 straight pi

    • The graph then repeats itself

3-4-1-ib-ai-hl-unit-circle-sine-graph-diagram-1
Construction of the cosine graph from the unit circle

How can I use the unit circle to construct the cosine graph?

  • The x-coordinates of the points on the unit circle give the values of cosine

  • You can plot the x-coordinates against the angles to form the cosine graph

  • You should remember the general shape

    • The cosine graph starts at 1

    • It then decreases and is equal to 0 when the angle is straight pi over 2

    • It continues to decrease and is equal to -1 when the angle is straight pi

    • It then increases and is returns to 0 when the angle is fraction numerator 3 straight pi over denominator 2 end fraction

    • It continues to increase and returns to 1 when the angle is 2 straight pi

    • The graph then repeats itself

Unit circle diagram with x-coordinates mapped to y-coordinates on a cosine graph, showing angles 0 to 2π. Arrows indicate coordinate transitions.
Construction of the cosine graph from the unit circle

Worked Example

The coordinates of a point on a unit circle, to 3 significant figures, are (0.629, 0.777). The radius from the centre to the point forms the angle θ° between the positive x-axis. Find θ° to the nearest degree.

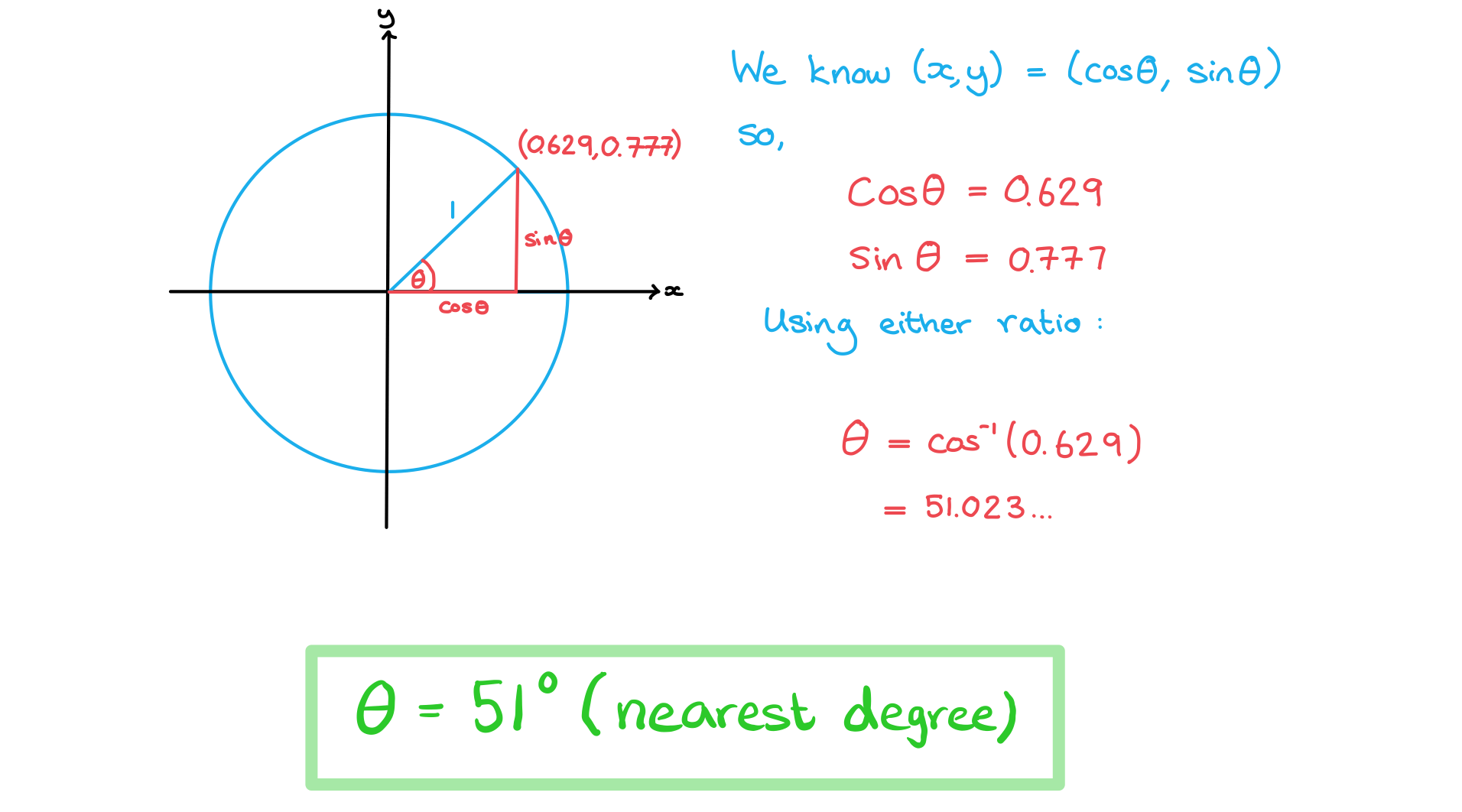
efewCfDn_aa-sl-3-4-1-defining-sin-and-cos-we-solution-1

Using the unit circle

When are sin, cos and tan positive?

  • The unit circle can be split into four quadrants at every 90°

    • The first quadrant is for angles between 0 and 90° 

      • All three of sinθ, cosθ and tanθ are positive in this quadrant

    • The second quadrant is for angles between 90° and 180°

      • sinθ is positive in this quadrant

    • The third quadrant is for angles between 180° and 270°

      • tanθ is positive in this quadrant

    • The fourth quadrant is for angles between 270° and 360°

      • cosθ is positive in this quadrant

Examiner Tips and Tricks

I tell my students to remember the phrase "All students take calculus" to help them remember the order.

What are the symmetries of the unit circle?

  • You can find symmetries by comparing the points on the unit circles which form the angles

    • theta

    • 180 minus theta

    • 180 plus theta

    • 360 minus theta

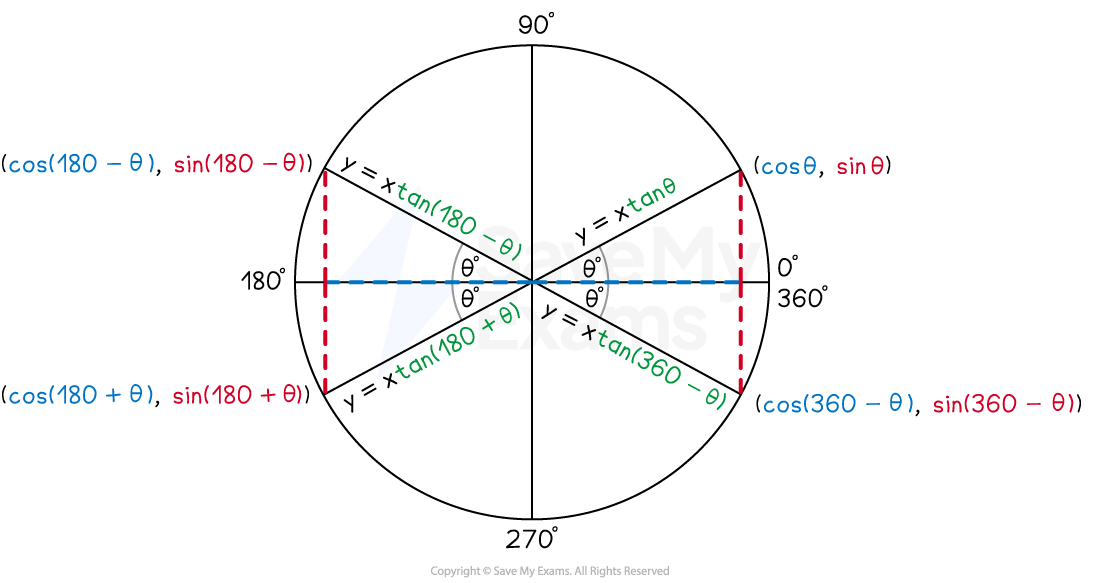
Unit circle diagram showing angles 0°, 90°, 180°, 270°, and 360°, with trigonometric functions and tangent equations in each quadrant.
The symmetries of the trig ratios using the unit circle

open parentheses 180 minus theta close parentheses

open parentheses 180 plus theta close parentheses

open parentheses 360 minus theta close parentheses

sin

sin open parentheses 180 minus theta close parentheses equals sin theta

sin open parentheses 180 plus theta close parentheses equals negative sin theta

sin open parentheses 360 minus theta close parentheses equals negative sin theta

cos

cos open parentheses 180 minus theta close parentheses equals negative cos theta

cos open parentheses 180 plus theta close parentheses equals negative cos theta

cos open parentheses 360 minus theta close parentheses equals cos theta

tan

tan open parentheses 180 minus theta close parentheses equals negative tan theta

tan open parentheses 180 plus theta close parentheses equals tan theta

tan open parentheses 360 minus theta close parentheses equals negative tan theta

  • Adding 360° does not change the trig ratio

    • sin open parentheses 360 plus theta close parentheses equals sin theta

    • cos open parentheses 360 plus theta close parentheses equals cos theta

    • tan open parentheses 360 plus theta close parentheses equals tan theta

  • negative theta gives the same ratios as 360 minus theta

    • sin open parentheses negative theta close parentheses equals negative sin theta

    • cos open parentheses negative theta close parentheses equals cos theta

    • tan open parentheses negative theta close parentheses equals negative tan theta

How can I find the value of sin, cos and tan using the symmetries of the unit circle?

  • You can write a trig ratio of any angle in terms of a trig ratio of an acute angle

  • Compare the angle to 180° or 360° and use the symmetries

  • For example: 210° = 180° + 30°

    • sin 210 equals negative sin 30

    • cos 210 equals negative cos 30

    • tan 210 equals tan 30

  • For example: 315° = 360° - 45°

    • sin 315 equals negative sin 45

    • cos 315 equals cos 45

    • tan 315 equals negative tan 45

How can I use the unit circle to find solutions to simple trigonometric equations?

  • STEP 1
    Use the inverse trig buttons on your calculator to find the principal value

    • e.g. to solve sin x equals 0.5, type in sin to the power of negative 1 end exponent open parentheses 0.5 close parentheses

  • STEP 2
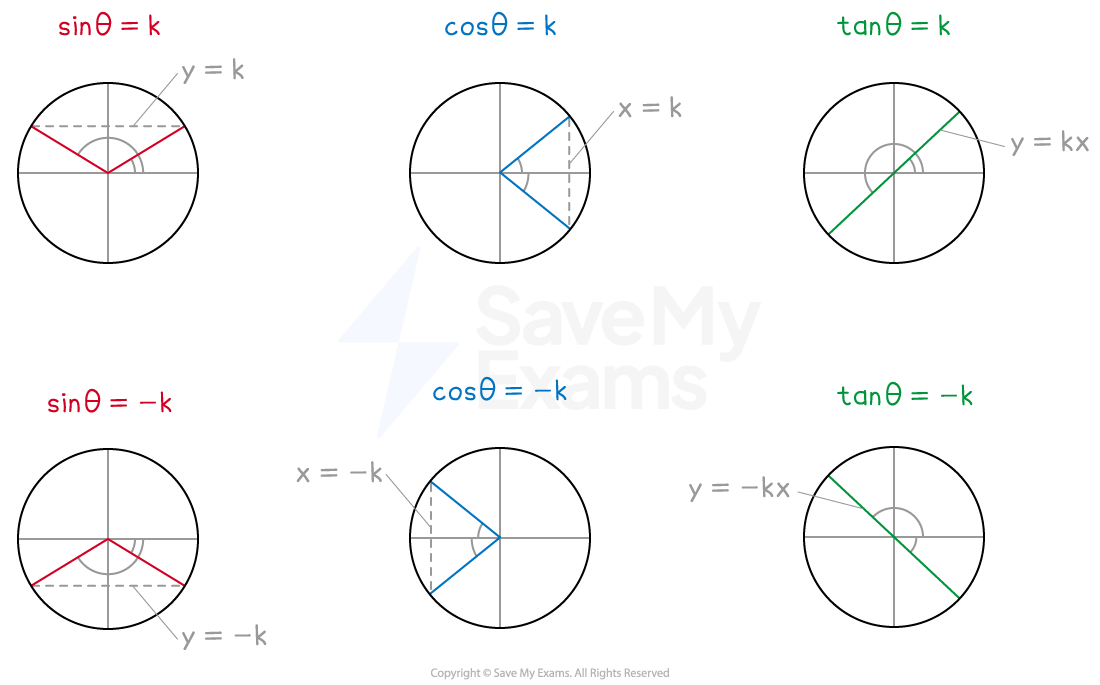
    Label this point on the unit circle and draw the radius

  • STEP 3
    Find the second point on the unit circle that also leads to a solution and draw the radius

    • For the equation sin x equals k

      • The second point has the same y-coordinate

      • It is in the quadrant horizontal to the quadrant with the first radius

    • For the equation cos x equals k

      • The second point has the same x-coordinate

      • It is in the quadrant vertical to the quadrant with the first radius

    • For the equation tan x equals k

      • The second point has a radius with the same gradient

      • It is in the quadrant diagonal to the quadrant with the first radius

Diagram showing unit circles demonstrating equations sin(x)=k, cos(x)=k, tan(x)=k, sin(x)=-k, cos(x)=-k, tan(x)=-k with coloured angles.

  • STEP 4
    Find the angle from the positive x-axis to the second radius using symmetries

    • e.g. sin open parentheses 30 close parentheses equals sin open parentheses 150 close parentheses and sin open parentheses negative 60 close parentheses equals sin open parentheses negative 120 close parentheses

    • e.g. cos open parentheses 30 close parentheses equals cos open parentheses negative 30 close parentheses and cos open parentheses 120 close parentheses equals cos open parentheses 240 close parentheses

    • e.g. tan open parentheses 30 close parentheses equals tan open parentheses 210 close parentheses and tan open parentheses negative 60 close parentheses equals tan open parentheses 120 close parentheses

  • STEP 5
    Use the two angles to find all solutions in the given interval

    • Add or subtract multiples of 360° from the two angles

Examiner Tips and Tricks

The question could ask you to find the solutions in radians, so make sure you remember the main angles:

  • 180° = π radians

  • 360° = 2π radians

Worked Example

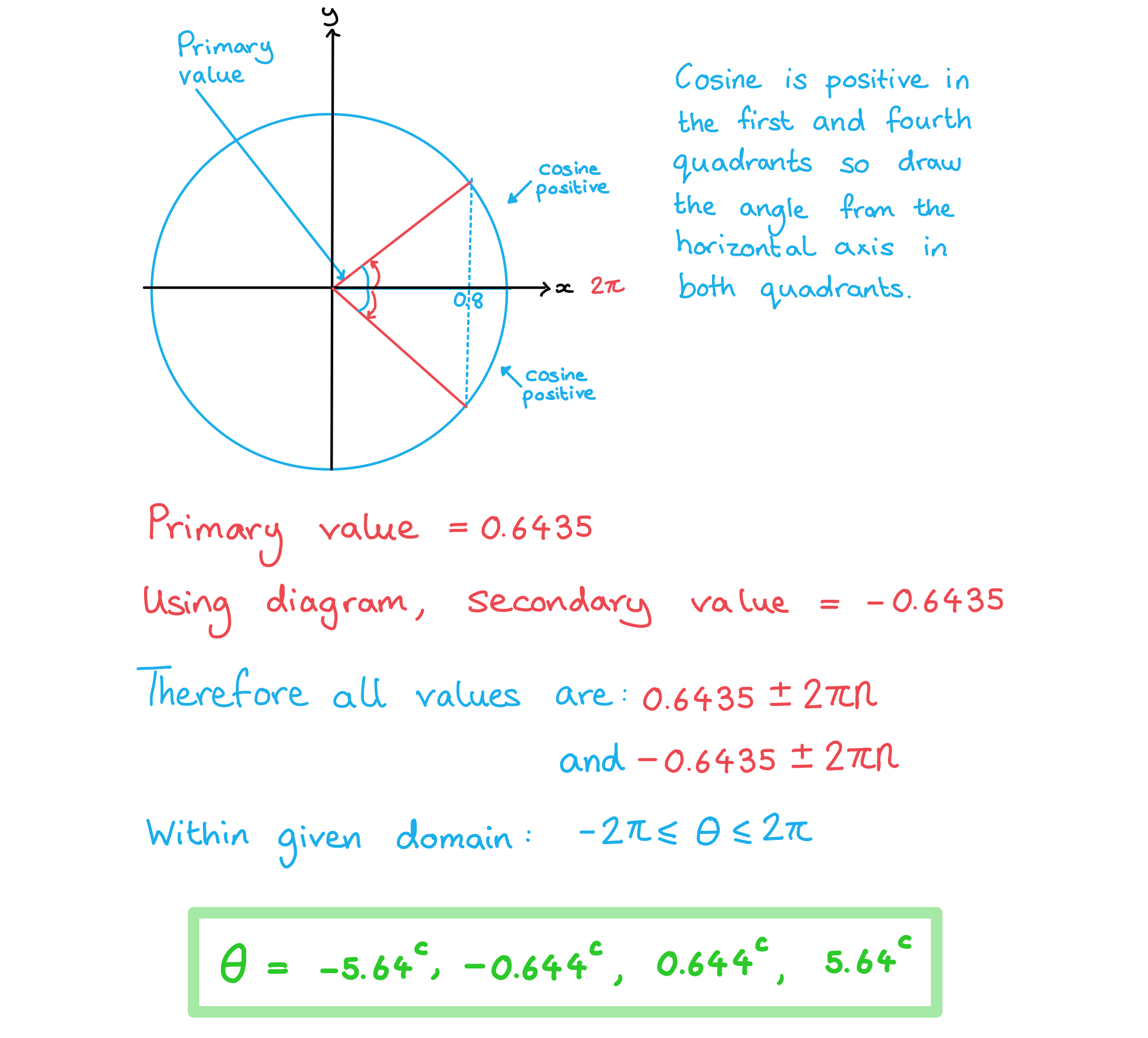
Given that one solution of cosθ = 0.8 is θ = 0.6435 radians correct to 4 decimal places, find all other solutions in the range -2π ≤ θ ≤ 2π.  Give your answers correct to 3 significant figures.

aa-sl-3-4-1-using-the-unit-circle-we-solution-2

You've read 0 of your 5 free revision notes this week

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards
    Previous:Bearings & ConstructionsNext:Exact Values
    Author
    Reviewer
    Amber

    Author: Amber

    Expertise: Maths Content Creator

    Amber gained a first class degree in Mathematics & Meteorology from the University of Reading before training to become a teacher. She is passionate about teaching, having spent 8 years teaching GCSE and A Level Mathematics both in the UK and internationally. Amber loves creating bright and informative resources to help students reach their potential.

    Dan Finlay

    Reviewer: Dan Finlay

    Expertise: Maths Subject Lead

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.