Did this video help you?
Pythagoras & Right-Angled Trigonometry (DP IB Maths: AA SL): Revision Note
Pythagoras
What is the Pythagorean theorem?
- Pythagoras’ theorem is a formula that works for right-angled triangles only
- It states that for any right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the two shorter sides
- The hypotenuse is the longest side in a right-angled triangle
- It will always be opposite the right angle
- If we label the hypotenuse c, and label the other two sides a and b, then Pythagoras’ theorem tells us that
- The hypotenuse is the longest side in a right-angled triangle
- The formula for Pythagoras’ theorem is assumed prior knowledge and is not in the formula booklet
- You will need to remember it
How can we use Pythagoras’ theorem?
- If you know two sides of any right-angled triangle you can use Pythagoras’ theorem to find the length of the third side
- Substitute the values you have into the formula and either solve or rearrange
- To find the length of the hypotenuse you can use:
- To find the length of one of the other sides you can use:
or
- Note that when finding the hypotenuse you should add inside the square root and when finding one of the other sides you should subtract inside the square root
- Always check your answer carefully to make sure that the hypotenuse is the longest side
- Note that Pythagoras’ theorem questions will rarely be standalone questions and will often be ‘hidden’ in other geometry questions
What is the converse of the Pythagorean theorem?
- The converse of the Pythagorean theorem states that if
is true then the triangle must be a right-angled triangle
- This is a very useful way of determining whether a triangle is right-angled
- If a diagram in a question does not clearly show that something is right-angled, you may need to use Pythagoras’ theorem to check
Examiner Tip
- Pythagoras' theorem pops up in lots of exam questions so bear it in mind whenever you see a right-angled triangle in an exam question!
Worked example
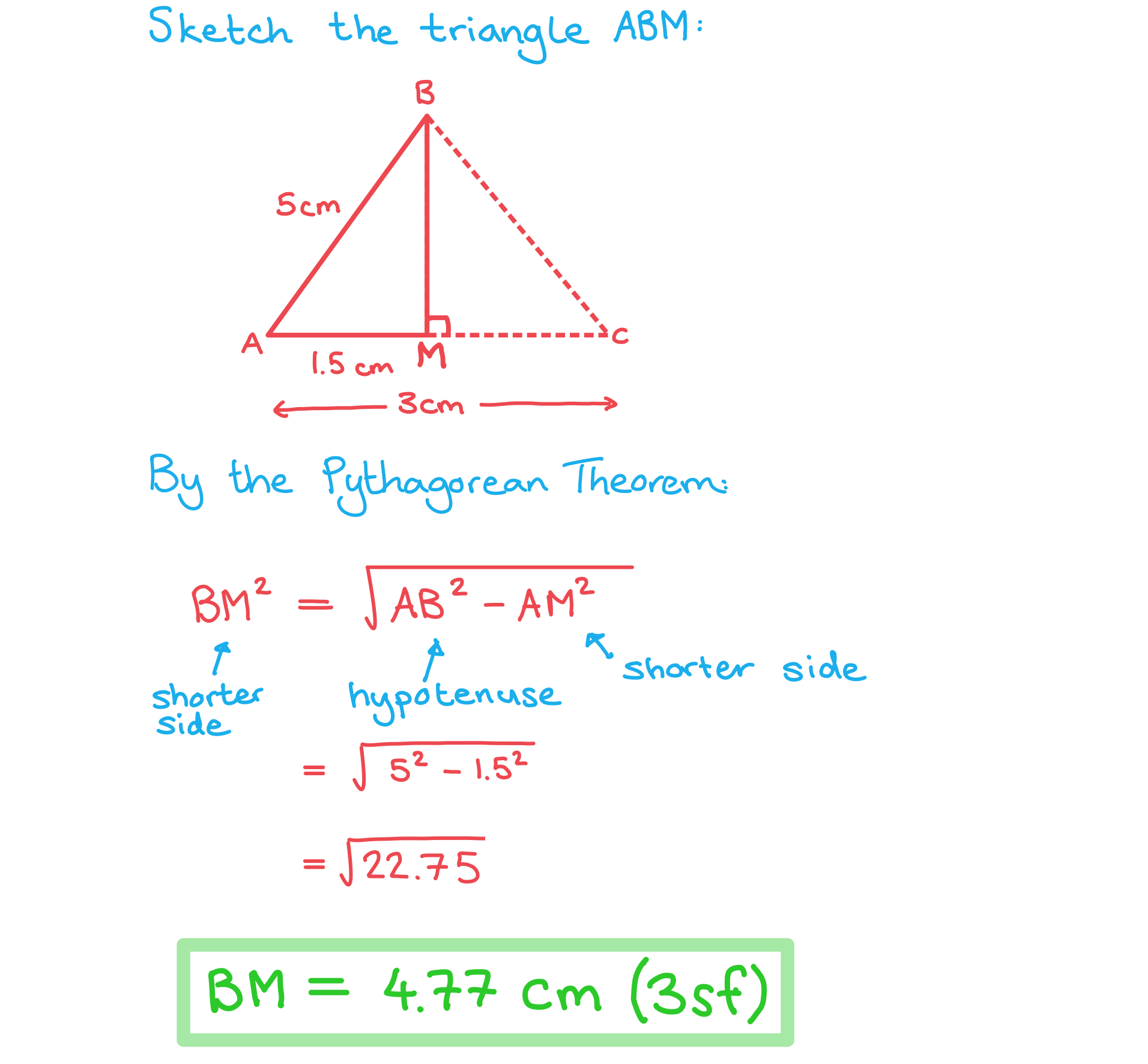
ABCDEF is a chocolate bar in the shape of a triangular prism. The end of the chocolate bar is an isosceles triangle where AC = 3 cm and AB = BC = 5 cm. M is the midpoint of AC. This information is shown in the diagram below.
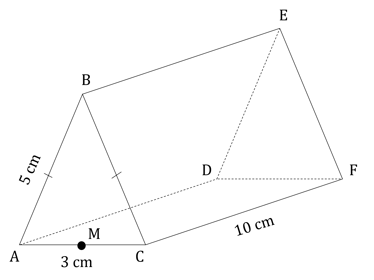
Calculate the length BM.
Did this video help you?
Right-Angled Trigonometry
What is Trigonometry?
- Trigonometry is the mathematics of angles in triangles
- It looks at the relationship between side lengths and angles of triangles
- It comes from the Greek words trigonon meaning ‘triangle’ and metron meaning ‘measure’
What are Sin, Cos and Tan?
- The three trigonometric functions Sine, Cosine and Tangent come from ratios of side lengths in right-angled triangles
- To see how the ratios work you must first label the sides of a right-angled triangle in relation to a chosen angle
- The hypotenuse, H, is the longest side in a right-angled triangle
- It will always be opposite the right angle
- If we label one of the other angles θ, the side opposite θ will be labelled opposite, O, and the side next to θ will be labelled adjacent, A
- The hypotenuse, H, is the longest side in a right-angled triangle
- The functions Sine, Cosine and Tangent are the ratios of the lengths of these sides as follows
-
- These are not in the formula book, you must remember them
- The mnemonic SOHCAHTOA is often used as a way of remembering which ratio is which
- Sin is Opposite over Hypotenuse
- Cos is Adjacent over Hypotenuse
- Tan is Opposite over Adjacent

How can we use SOHCAHTOA to find missing lengths?
- If you know the length of one of the sides of any right-angled triangle and one of the angles you can use SOHCAHTOA to find the length of the other sides
- Always start by labelling the sides of the triangle with H, O and A
- Choose the correct ratio by looking only at the values that you have and that you want
- For example if you know the angle and the side opposite it (O) and you want to find the hypotenuse (H) you should use the sine ratio
- Substitute the values into the ratio
- Use your calculator to find the solution
How can we use SOHCAHTOA to find missing angles?
- If you know two sides of any right-angled triangle you can use SOHCAHTOA to find the size of one of the angles
- Missing angles are found using the inverse functions:
,
,
- After choosing the correct ratio and substituting the values use the inverse trigonometric functions on your calculator to find the correct answer
Examiner Tip
- You need to remember the sides involved in the different trig ratios as they are not given to you in the exam
Worked example
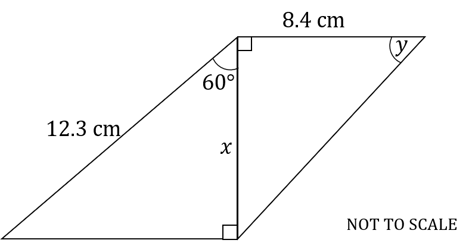
Find the values of and
in the following diagram. Give your answers to 3 significant figures.

Did this video help you?
3D Problems
How does Pythagoras work in 3D?
- 3D shapes can often be broken down into several 2D shapes
- With Pythagoras’ Theorem you will be specifically looking for right-angled triangles
- The right-angled triangles you need will have two known sides and one unknown side
- Look for perpendicular lines to help you spot right-angled triangles
- There is a 3D version of the Pythagorean theorem formula:
-
- However it is usually easier to see a problem by breaking it down into two or more 2D problems
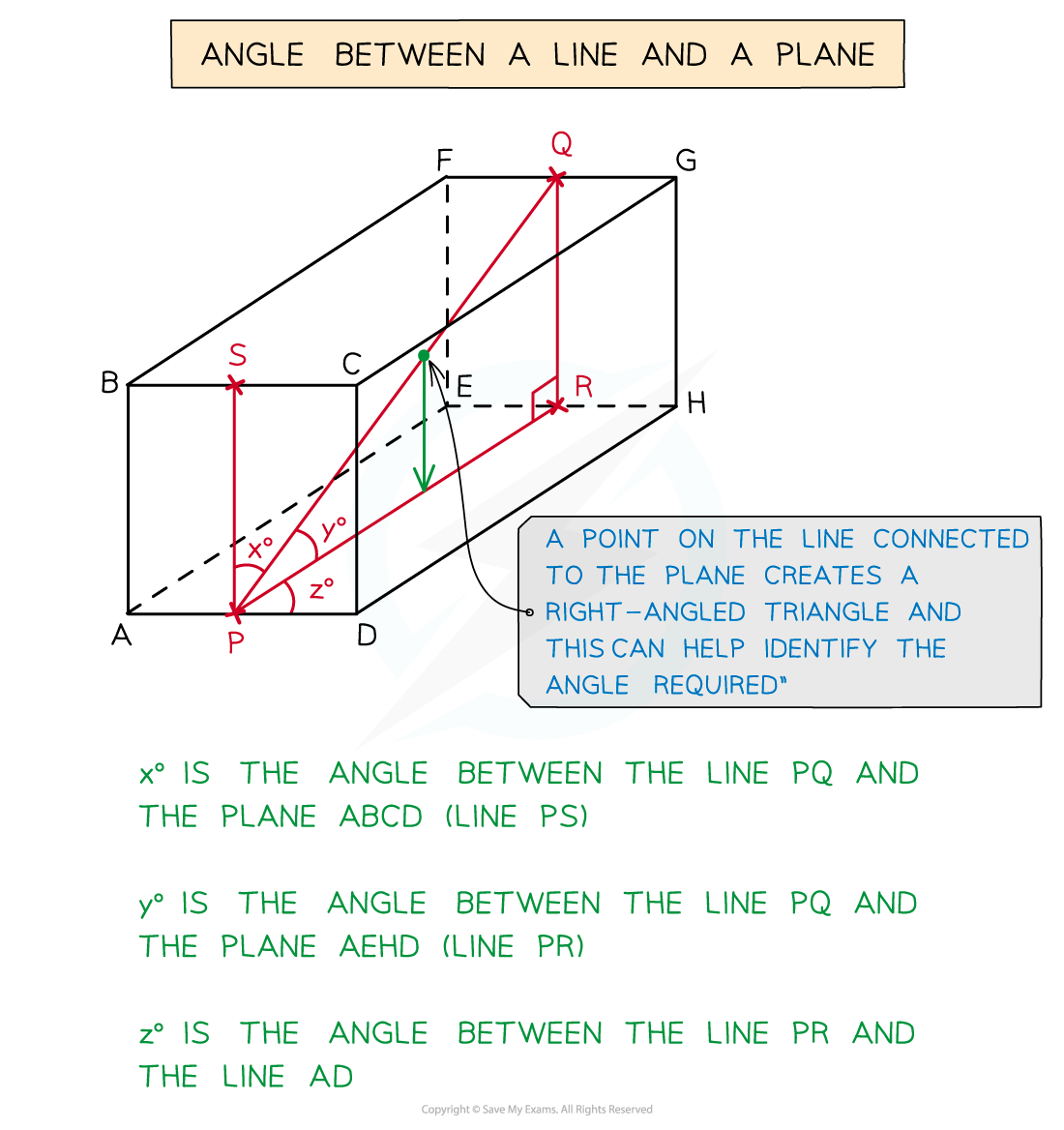
How does SOHCAHTOA work in 3D?
- Again look for a combination of right-angled triangles that would lead to the missing angle or side
- The angle you are working with can be awkward in 3D
- The angle between a line and a plane is not always obvious
- If unsure put a point on the line and draw a new line to the plane
- This should create a right-angled triangle
Examiner Tip
- Annotate diagrams that are given to you with values that you have calculated
- It can be useful to make additional sketches of parts of any diagrams that are given to you, especially if there are multiple lengths/angles that you are asked to find
- If you are not given a diagram, sketch a nice, big, clear one!
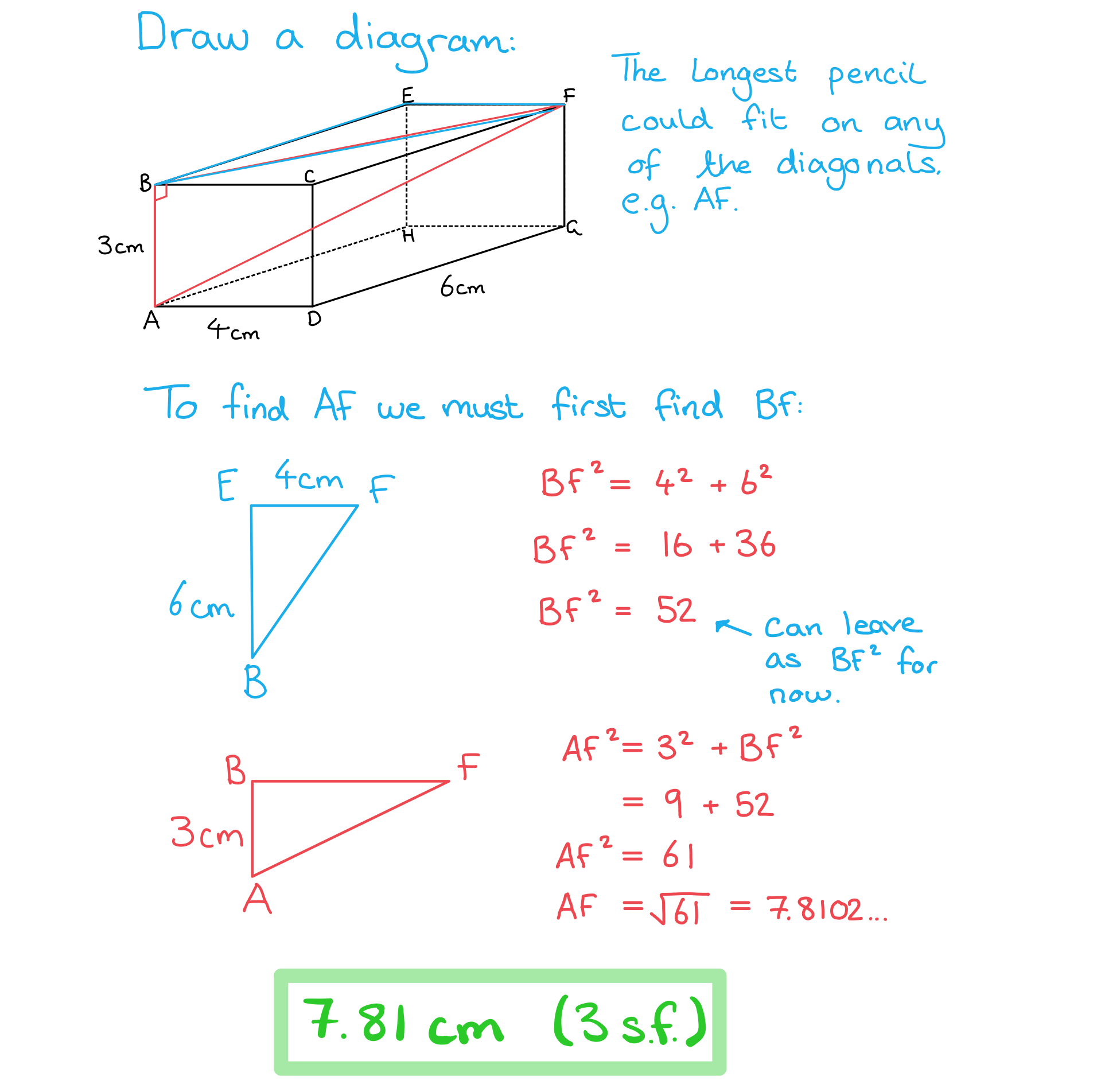
Worked example
A pencil is being put into a cuboid shaped box. The base of the box has a width of 4 cm and a length of 6 cm. The height of the box is 3 cm. Find:


You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
