Revision NotesExam QuestionsFlashcards
IBMaths: AA SLDPRevision Notes2. Functions2.4 Further Functions & Graphs2.4.2 Exponential & Logarithmic Functions

Exponential & Logarithmic Functions (DP IB Maths: AA SL)

Revision Note

Dan

Author

Dan

Last updated

Did this video help you?

Exponential Functions & Graphs

What is an exponential function?

  • An exponential function is defined by space f left parenthesis x right parenthesis equals a to the power of x comma space a greater than 0
  • Its domain is the set of all real values
  • Its range is the set of all positive real values
  • An important exponential function is space f left parenthesis x right parenthesis equals straight e to the power of x
    • Where e is the mathematical constant 2.718…
  • Any exponential function can be written using e
    • a to the power of x equals straight e to the power of x ln a end exponent
      • This is given in the formula booklet

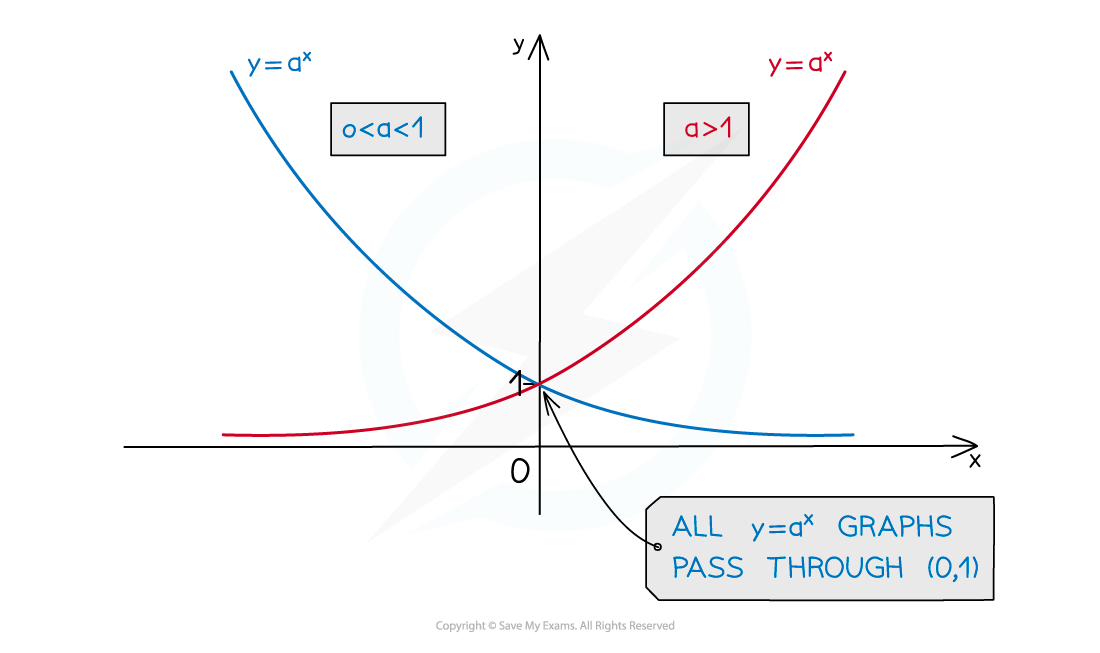
What are the key features of exponential graphs?

  • The graphs have a y-intercept at (0, 1)
  • The graph will always pass through the point (1, a)
  • The graphs do not have any roots
  • The graphs have a horizontal asymptote at the x-axis: space y equals 0
    • For a > 1 this is the limiting value when x tends to negative infinity
    • For 0 < a < 1 this is the limiting value when x tends to positive infinity
  • The graphs do not have any minimum or maximum points

Exponential Functions fig1

e Notes fig1

 

6-1-1-notes-fig4

Did this video help you?

Logarithmic Functions & Graphs

What is a logarithmic function?

  • A logarithmic function is of the form space f left parenthesis x right parenthesis equals log subscript a x comma space x greater than 0
  • Its domain is the set of all positive real values
    • You can't take a log of zero or a negative number
  • Its range is set of all real values
  • log subscript a x and a to the power of x are inverse functions
  • An important logarithmic function is space f left parenthesis x right parenthesis equals ln space x
    • This is the natural logarithmic function ln space x identical to log subscript straight e x
    • This is the inverse of straight e to the power of x
      • ln space straight e to the power of x equals xand straight e to the power of ln space x end exponent equals x
  • Any logarithmic function can be written using ln
    • log subscript a x equals fraction numerator ln space x over denominator ln space a end fractionusing the change of base formula

What are the key features of logarithmic graphs?

  • The graphs do not have a y-intercept
  • The graphs have one root at (1, 0)
  • The graphs will always pass through the point (a, 1)
  • The graphs have a vertical asymptote at the y-axis: x equals 0
  • The graphs do not have any minimum or maximum points

Worked example

The function space f is defined by space f left parenthesis x right parenthesis equals log subscript 5 x for x greater than 0.

a)
Write down the inverse of space f. Give your answer in the form straight e to the power of g left parenthesis x right parenthesis end exponent.

2-4-2-ib-aa-sl-log-function-a-we-solution

b)
Sketch the graphs of space f and its inverse on the same set of axes.

2-4-2-ib-aa-sl-log-function-b-we-solution

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards

    Did this page help you?

    Previous:2.4.1 Reciprocal & Rational FunctionsNext:2.4.3 Solving Equations
    Dan

    Author: Dan

    Expertise: Maths

    Dan graduated from the University of Oxford with a First class degree in mathematics. As well as teaching maths for over 8 years, Dan has marked a range of exams for Edexcel, tutored students and taught A Level Accounting. Dan has a keen interest in statistics and probability and their real-life applications.