Language of Functions (DP IB Maths: AA SL): Revision Note

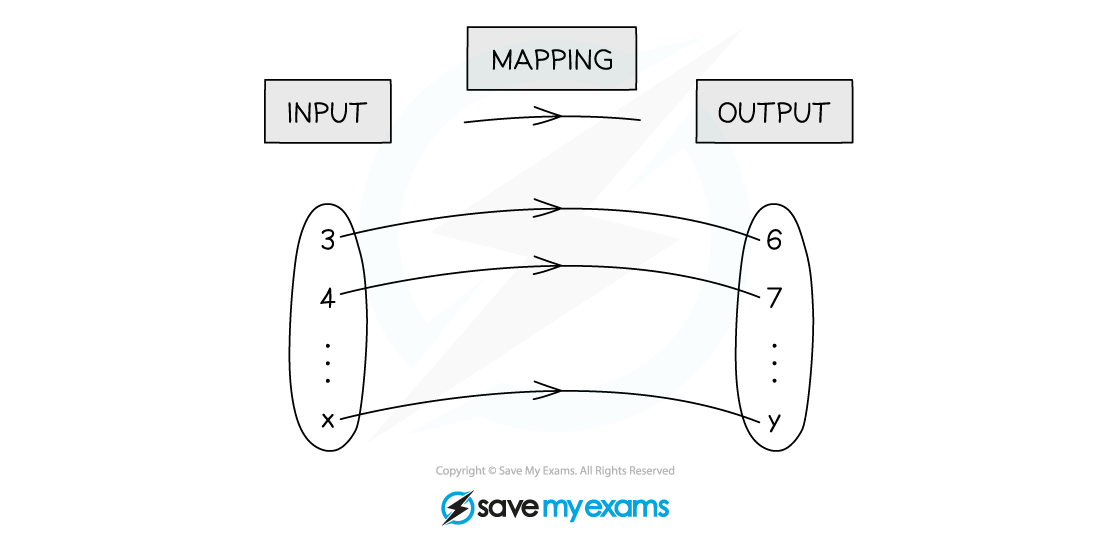
What is a mapping?

• A mapping transforms one set of values (inputs) into another set of values (outputs)
• Mappings can be:
  • One-to-one
    • Each input gets mapped to exactly one unique output
    • No two inputs are mapped to the same output
    • For example: A mapping that cubes the input
  • Many-to-one
    • Each input gets mapped to exactly one output
    • Multiple inputs can be mapped to the same output
    • For example: A mapping that squares the input
  • One-to-many
    • An input can be mapped to more than one output
    • No two inputs are mapped to the same output
    • For example: A mapping that gives the numbers which when squared equal the input
  • Many-to-many
    • An input can be mapped to more than one output
    • Multiple inputs can be mapped to the same output
    • For example: A mapping that gives the factors of the input

What is a function?

• A function is a mapping between two sets of numbers where each input gets mapped to exactly one output
  • The output does not need to be unique

• One-to-one and many-to-one mappings are functions
• A mapping is a function if its graph passes the vertical line test
  • Any vertical line will intersect with the graph at most once

What notation is used for functions?

• Functions are denoted using letters (such as  etc)
  • A function is followed by a variable in a bracket
  • This shows the input for the function
  • The letter is used most commonly for functions and will be used for the remainder of this revision note
• represents an expression for the value of the function when evaluated for the variable
• Function notation gets rid of the need for words which makes it universal
  • when can simply be written as 

What are the domain and range of a function?

• The domain of a function is the set of values that are used as inputs
• A domain should be stated with a function
  • If a domain is not stated then it is assumed the domain is all the real values which would work as inputs for the function
  • Domains are expressed in terms of the input
    • 
• The range of a function is the set of values that are given as outputs
  • The range depends on the domain
  • Ranges are expressed in terms of the output
    • 
• To graph a function we use the inputs as the x-coordinates and the outputs as the y-coordinates
  • corresponds to the coordinates (2, 5)
• Graphing the function can help you visualise the range
• Common sets of numbers have special symbols:
  • represents all the real numbers that can be placed on a number line
    • means is a real number
  • represents all the rational numbers where a and b are integers and b ≠ 0
  • represents all the integers (positive, negative and zero)
    • represents positive integers
  • represents the natural numbers (0,1,2,3...)

What are piecewise functions?

• Piecewise functions are defined by different functions depending on which interval the input is in
  • E.g. 
• The region for the individual functions cannot overlap
• To evaluate a piecewise function for a particular value
  • Find which interval includes 
  • Substitute into the corresponding function
• The function may or may not be continuous at the ends of the intervals
  • In the example above the function is
    • continuous at  as 
    • not continuous at  as