Factorising & Completing the Square (DP IB Analysis & Approaches (AA)) : Revision Note
Did this video help you?
Factorising Quadratics
Why is factorising quadratics useful?
Factorising gives roots (zeroes or solutions) of a quadratic
It gives the x-intercepts when drawing the graph
How do I factorise a monic quadratic of the form x2 + bx + c?
A monic quadratic is a quadratic where the coefficient of the x2 term is 1
You might be able to spot the factors by inspection
Especially if c is a prime number
Otherwise find two numbers m and n ..
A sum equal to b
A product equal to c
Rewrite bx as mx + nx
Use this to factorise x2 + mx + nx + c
A shortcut is to write:
How do I factorise a non-monic quadratic of the form ax2 + bx + c?
A non-monic quadratic is a quadratic where the coefficient of the x2 term is not equal to 1
If a, b & c have a common factor then first factorise that out to leave a quadratic with coefficients that have no common factors
You might be able to spot the factors by inspection
Especially if a and/or c are prime numbers
Otherwise find two numbers m and n ..
A sum equal to b
A product equal to ac
Rewrite bx as mx + nx
Use this to factorise ax2 + mx + nx + c
A shortcut is to write:
Then factorise common factors from numerator to cancel with the a on the denominator
How do I use the difference of two squares to factorise a quadratic of the form a2x2 - c2?
The difference of two squares can be used when...
There is no x term
The constant term is a negative
Square root the two terms
and
The two factors are the sum of square roots and the difference of the square roots
A shortcut is to write:
Examiner Tips and Tricks
You can deduce the factors of a quadratic function by using your GDC to find the solutions of a quadratic equation
Using your GDC, the quadratic equation
has solutions
and
Therefore the factors would be
and
i.e.
Worked Example
Factorise fully:
a) .

b) .
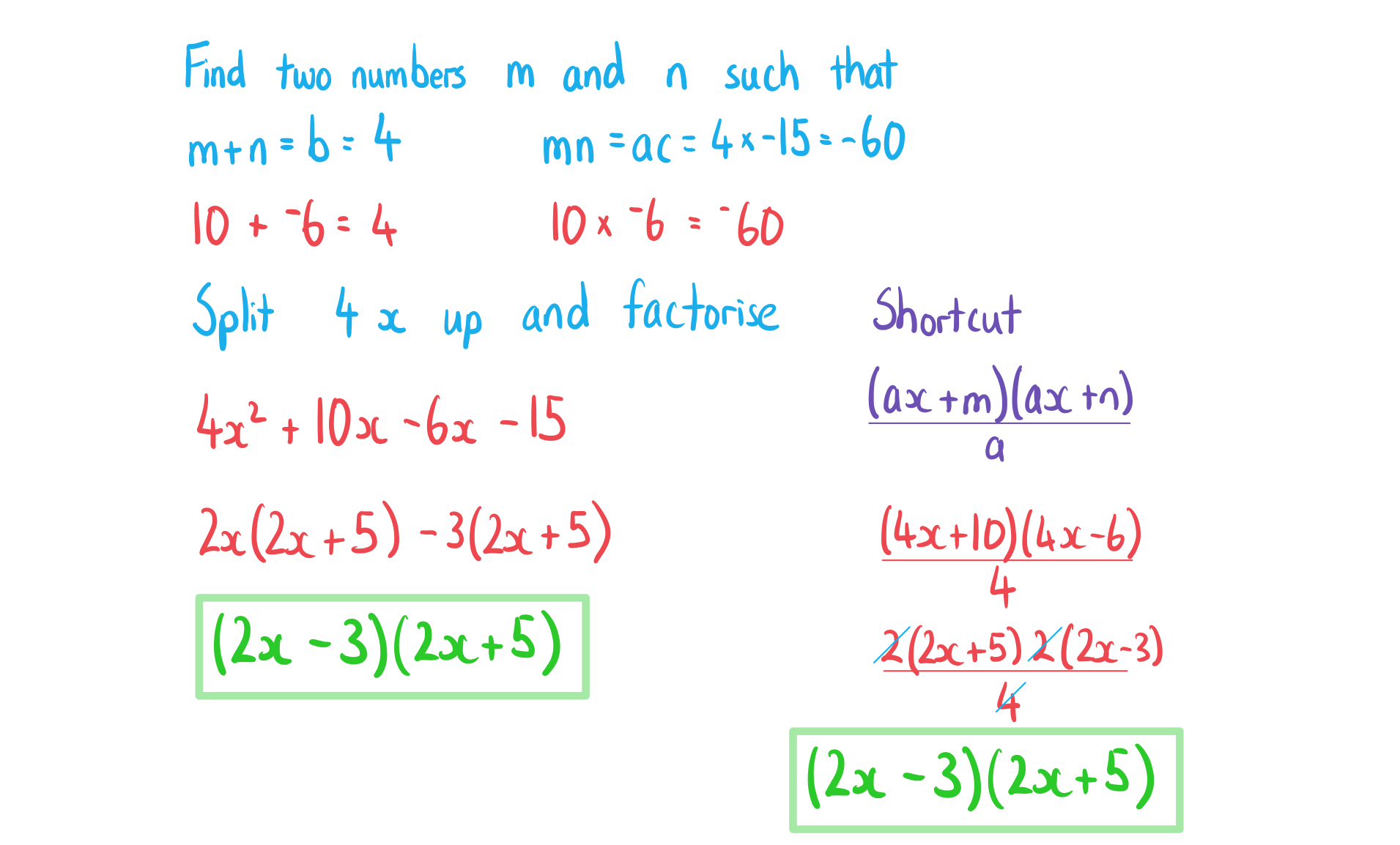
c) .

Did this video help you?
Completing the Square
Why is completing the square for quadratics useful?
Completing the square gives the maximum/minimum of a quadratic function
This can be used to define the range of the function
It gives the vertex when drawing the graph
It can be used to solve quadratic equations
It can be used to derive the quadratic formula
How do I complete the square for a monic quadratic of the form x2 + bx + c?
Half the value of b and write
This is because
Subtract the unwanted
term and add on the constant c
How do I complete the square for a non-monic quadratic of the form ax2 + bx + c?
Factorise out the a from the terms involving x
Leaving the c alone will avoid working with lots of fractions
Complete the square on the quadratic term
Half
and write
This is because
Subtract the unwanted
term
Multiply by a and add the constant c
Examiner Tips and Tricks
Some questions may not use the phrase "completing the square" so ensure you can recognise a quadratic expression or equation written in this form
Worked Example
Complete the square:
a) .
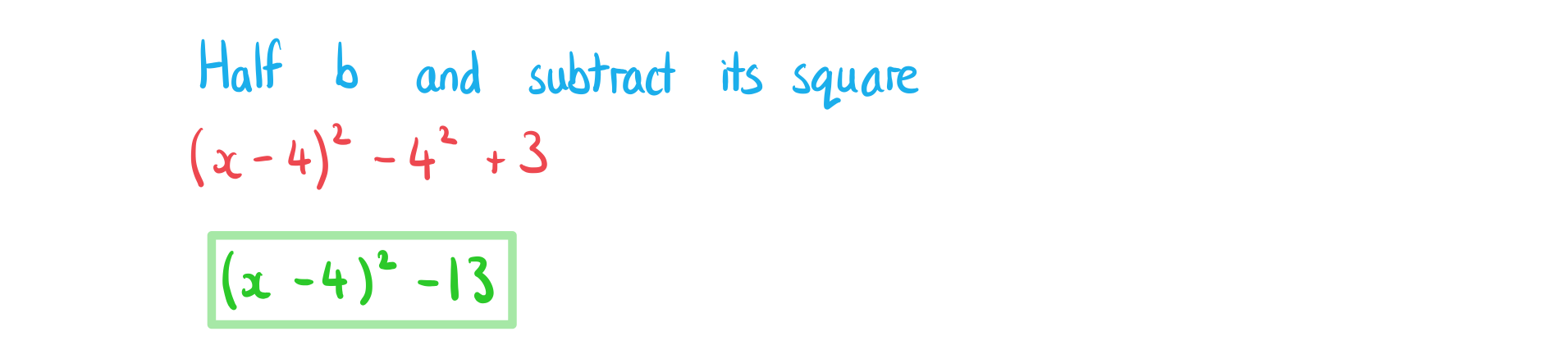
b) .
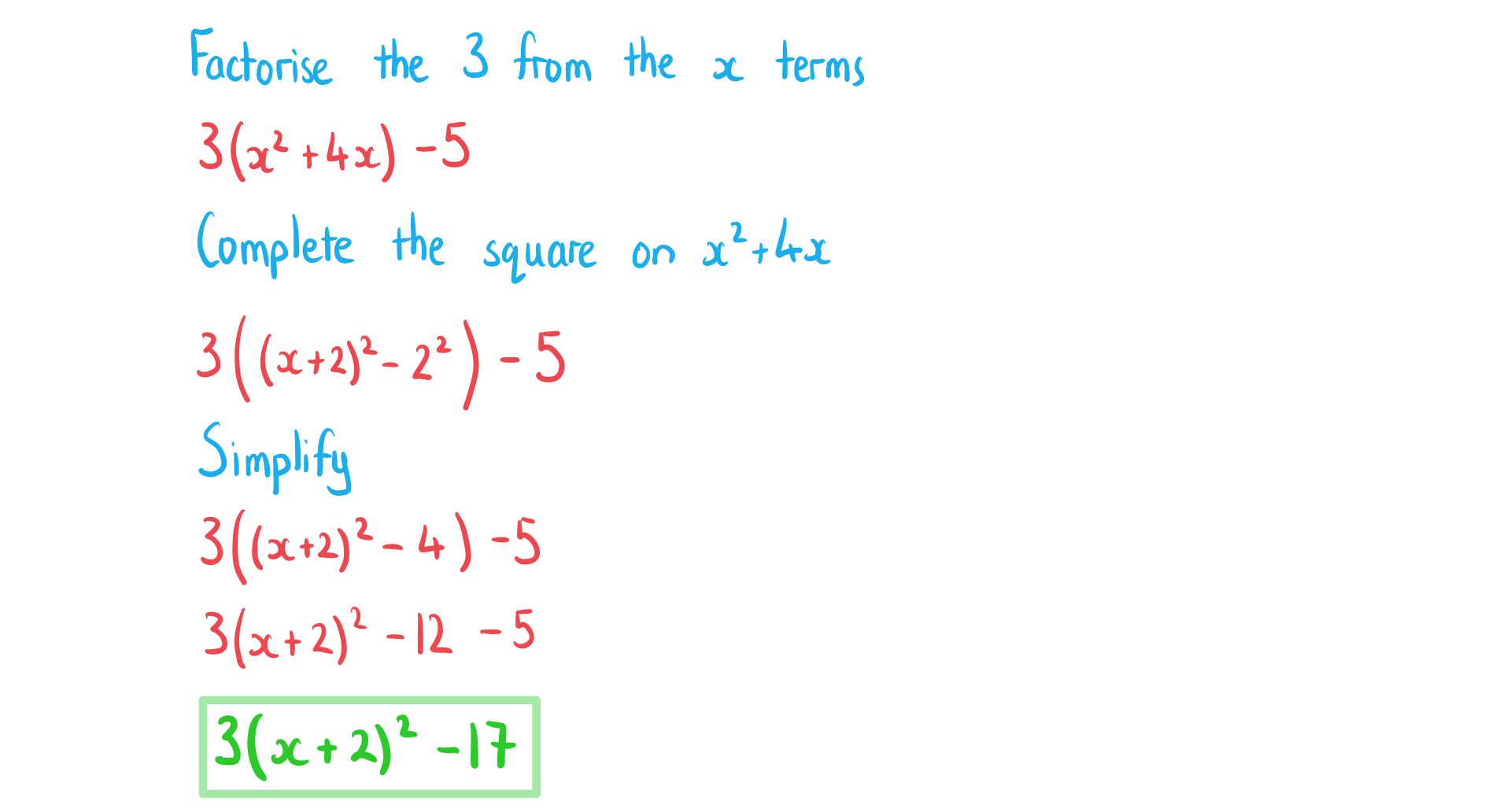

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?
