Below is the graph of a function , passing through the points P
, Q
, R
and S
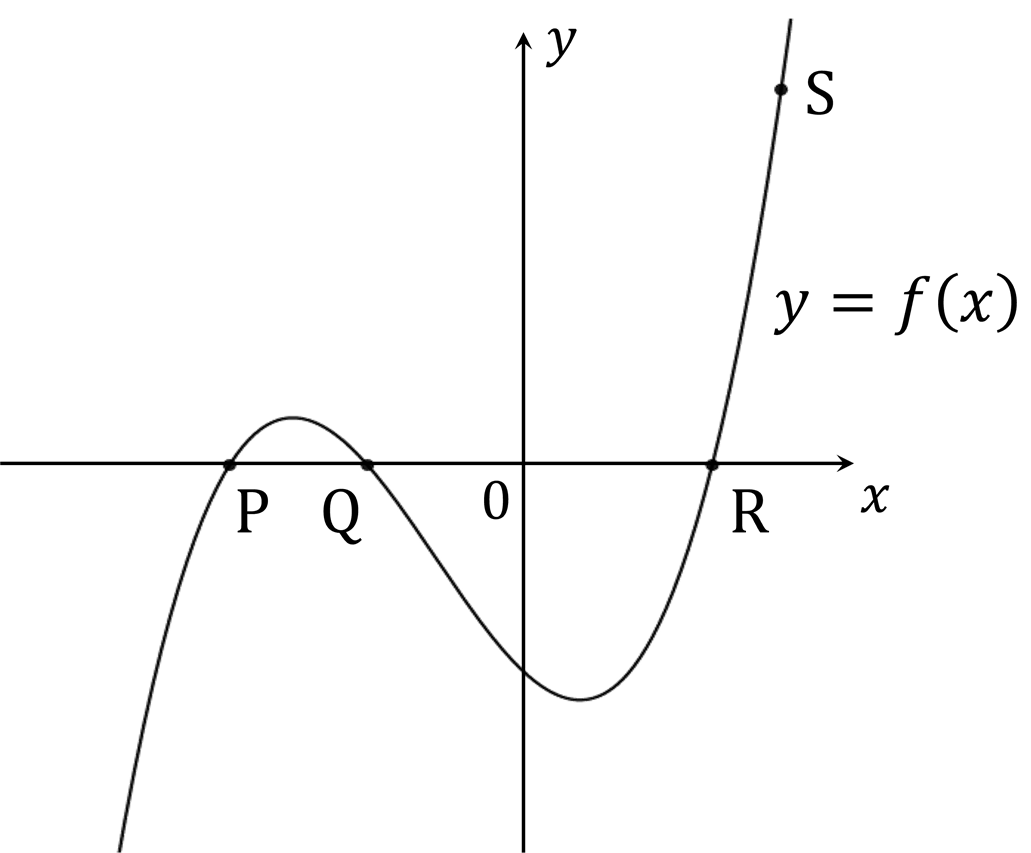
The function is translated vertically by the vector so that it passes through the point
.
Did this page help you?
Select a download format for 2.7 Polynomial Functions
Below is the graph of a function , passing through the points P
, Q
, R
and S

How did you do?
The function is translated vertically by the vector so that it passes through the point
.
How did you do?
Did this page help you?
How did you do?
How did you do?
How did you do?
Did this page help you?
Let a function be defined by
.
How did you do?
Did this page help you?
How did you do?
How did you do?
Did this page help you?
Consider the polynomial
How did you do?
How did you do?
Did this page help you?
Consider the function
How did you do?
Did this page help you?
The function has
as a factor, and when
is divided by
the remainder is 7.
How did you do?
How did you do?
Did this page help you?
Given that is one of the roots of the equation
find the other two roots.
How did you do?
Did this page help you?
How did you do?
How did you do?
Did this page help you?
For the function , the sum of the roots is
and the product of the roots is
. Find the values of
and
.
How did you do?
Did this page help you?
The function has three real and two complex roots.
How did you do?
It is given for that the sum of the roots is
and the product of the roots is
.
How did you do?
How did you do?
Did this page help you?
and
are non-real roots of the equation
, where
is a constant.
How did you do?
How did you do?
How did you do?
Did this page help you?
Consider the function , where
is a constant.
It is given that is a factor of
.
How did you do?
How did you do?
How did you do?
Did this page help you?
Consider the function , where
and
are constants. It is given that
is a factor of
.
How did you do?
How did you do?
Did this page help you?
is a zero of the function
where
is a constant.
How did you do?
How did you do?
The point is a turning point on the graph
.
How did you do?
Did this page help you?
The graph of is shown below, where
is a polynomial function. The graph passes through the points
and
.
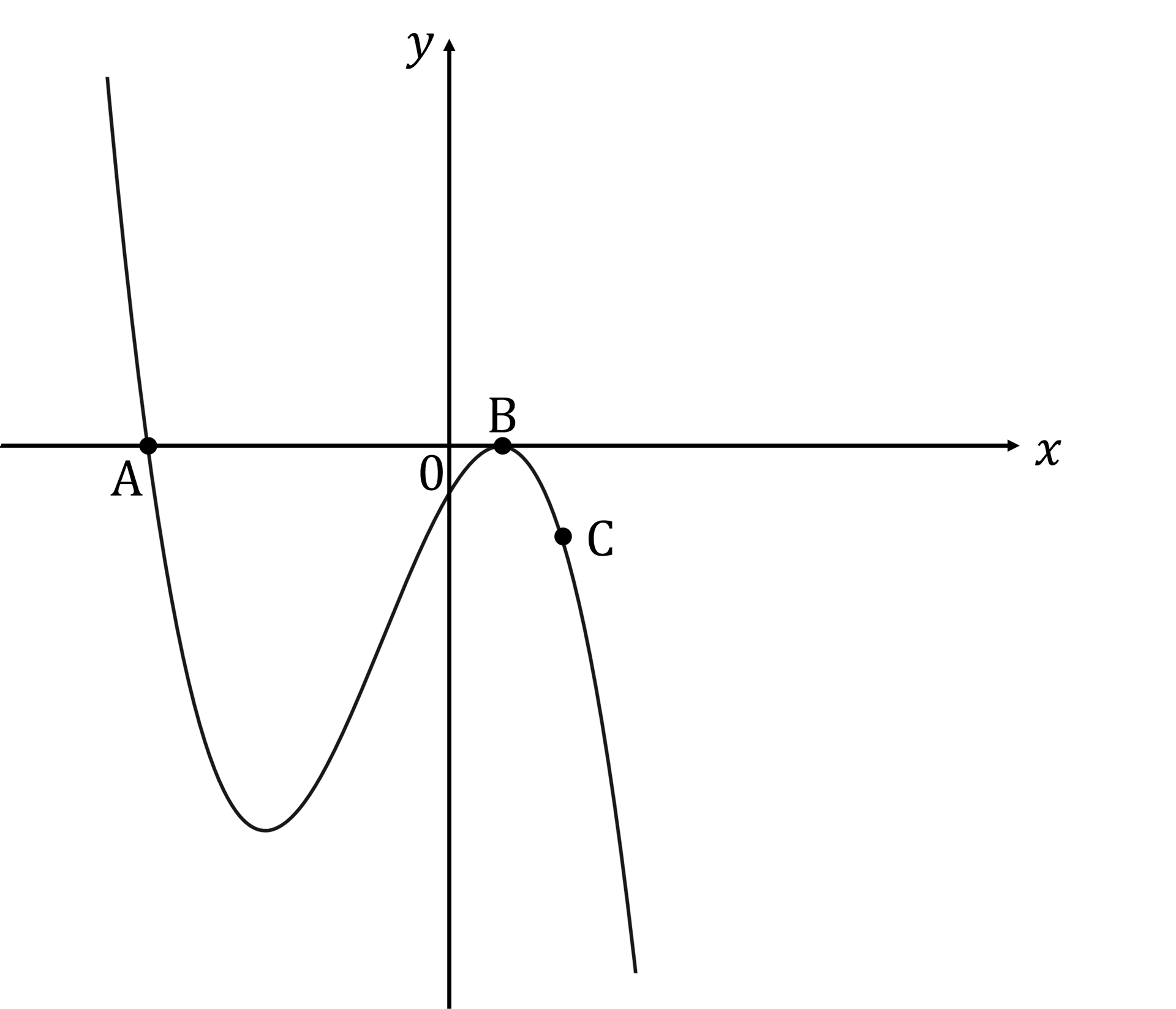
How did you do?
The graph is translated by the vector to form the graph
, where
is a constant and
is a polynomial.
How did you do?
Did this page help you?
Given that is a factor of the function
and that the remainder when
is divided by
is
, find the values of the constants p and q.
How did you do?
Did this page help you?
Show that can be written in the form
where
and
are constants to be found.
How did you do?
Did this page help you?
For the function , the sum of the roots is
and the product of the roots is
. Find all five roots of
.
How did you do?
Did this page help you?
and
are non-real solutions of the equation
.
Given that and
, find the value of
.
How did you do?
Did this page help you?
The function has two integer solutions, one of which is double the other one.
Find the value of .
How did you do?
Did this page help you?
Consider the function , where
and
are real constants.
How did you do?
How did you do?
Did this page help you?
Let be a polynomial defined by
How did you do?
Consider the function defined by
, where
is a real constant.
How did you do?
Did this page help you?
Consider the function , where
and
are constants. It is given that
is a factor of
.
How did you do?
How did you do?
Did this page help you?
Consider the function
where for
.
The graph of , shown below, passes through
. The roots of
are
and
.
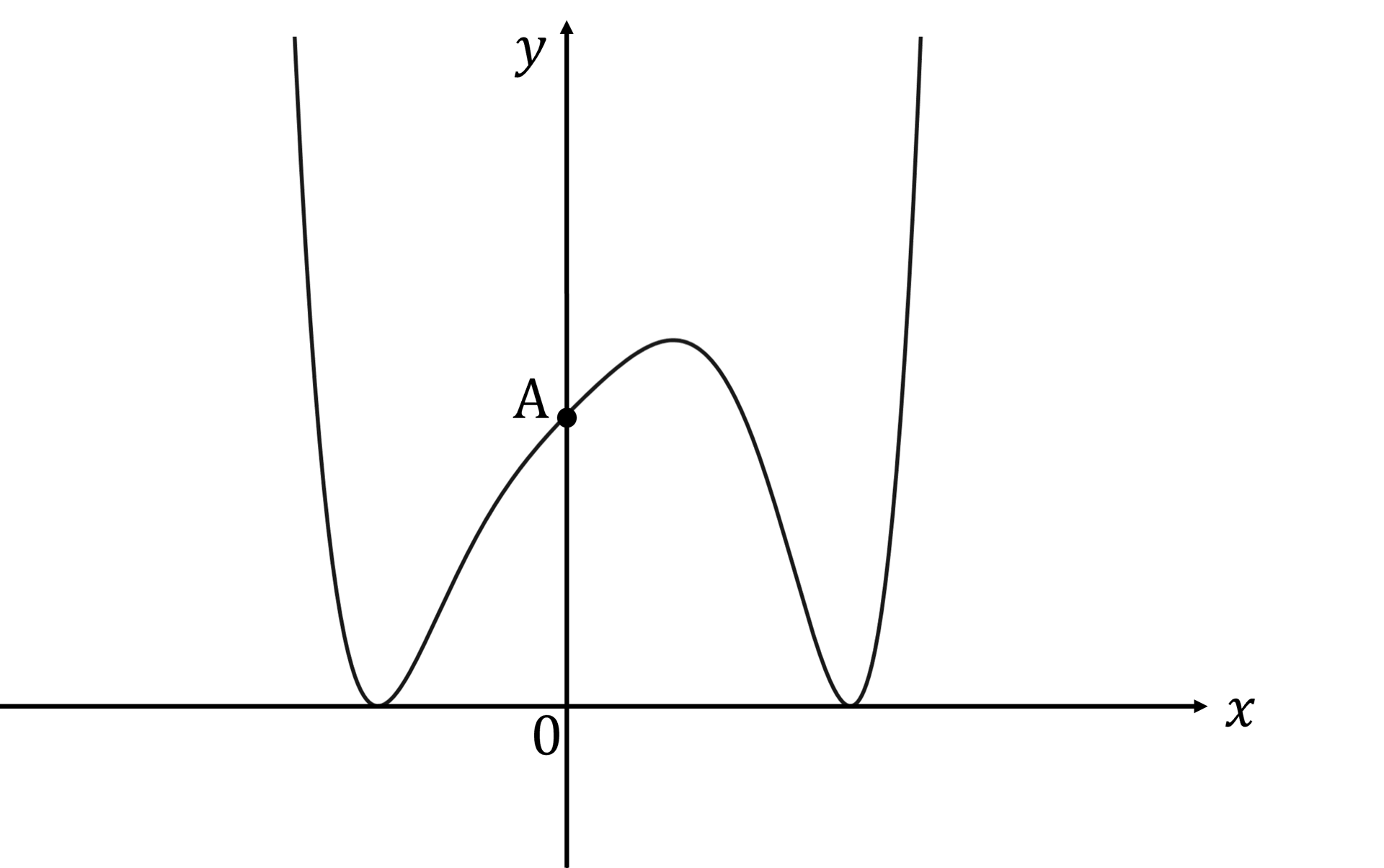
How did you do?
How did you do?
Did this page help you?
A polynomial function is defined by
where
and
are positive constants with
.
How did you do?
How did you do?
Consider the function , where
and
are positive constants. The points
and
lie on the graph
.
How did you do?
Did this page help you?
Consider the function defined by
, where
are constants.
Given that is a factor of
, and that the sum of the roots of the equation
is 5,
How did you do?
Did this page help you?
Consider the function defined by
, where
and
are real constants.
It is given that the sum of the roots of the equation is
, and that the product of the roots is
.
Find a set of values for and
that satisfies the above conditions, such that
. .
How did you do?
Did this page help you?
The equation has non-real roots
and
where
.
How did you do?
The equation has roots
and
.
How did you do?
Did this page help you?
Consider the polynomial function defined by
Where the are real constants. The function has the property that
for all values of
.
How did you do?
show that is also a root of
, and
hence find the values of and
in terms of
.
How did you do?
Did this page help you?
Consider the polynomial function , where
. Two distinct roots of
are given by
and
, where
is a real constant. The remainder when
is divided by
is 8100.
How did you do?
How did you do?
Did this page help you?
The polynomial function is defined by
where is a real constant.
The graph of only intersects the
-axis at the point
.
How did you do?
How did you do?
Did this page help you?