IBMaths: AA HLDPExam Questions1. Number & Algebra1.8 Complex Numbers

Complex Numbers (DP IB Maths: AA HL)

Exam Questions

4 hours33 questions
Medium
Hard
Very Hard
1a
Sme Calculator2 marks

Consider the complex numbers z subscript 1 equals 2 plus 2 straight i and z subscript 2 equals 2 plus 2 square root of 3 straight i.

Sketch z subscript 1 and z subscript 2 on the Argand diagram below, be sure to include an appropriate scale.

q1a_1-8_complex-numbers_medium_ib-maths-aa-hl

 

How did you do?

1b
Sme Calculator3 marks

Find the modulus of z subscript 1and z subscript 2.

How did you do?

1c
Sme Calculator3 marks

Find the argument of z subscript 1and z subscript 2.

How did you do?

Did this page help you?

2
Sme Calculator7 marks

Solve the following equations for x

(i)
x squared plus 4 x plus 5 equals 0

(ii)
x squared equals negative 625

(iii)
x to the power of 4 equals 24 space minus space 2 x squared.

How did you do?

Did this page help you?

3a
Sme Calculator2 marks

Let w subscript 1 equals z subscript 1 z subscript 2, where z subscript 1 equals 5 plus straight i and z subscript 2 equals 1 plus 2 straight i.

Express w in the form w equals a plus b straight i.

How did you do?

3b
Sme Calculator4 marks

Find the modulus and argument for w

How did you do?

Did this page help you?

4a
Sme Calculator3 marks

Let z equals w subscript 1 over w subscript 2, where w subscript 1 equals 4 minus straight i and w subscript 2 equals 1 minus 2 straight i.

Express z in the form z equals a plus b straight i.

How did you do?

4b
Sme Calculator4 marks

Find the modulus and argument for z.

How did you do?

Did this page help you?

5a
Sme Calculator2 marks

Consider the complex numbers z equals 3 minus 4 straight i and w equals 7 minus 2 straight i.

Find 

(i)
z plus w

(ii)
w minus z.

How did you do?

5b
Sme Calculator2 marks

Let z to the power of asterisk timesand w to the power of asterisk timesrepresent the complex conjugates of z and w, respectively.

Write down z to the power of asterisk timesand w to the power of asterisk times, giving your answers in the form a plus b straight i.

How did you do?

5c
Sme Calculator4 marks

Find

(i)
z to the power of asterisk times w

(ii)
w to the power of asterisk times over z.

How did you do?

Did this page help you?

6
Sme Calculator7 marks

Find all possible real values for a and b such that 

(i)
a plus b straight i equals 8 straight i

(ii)
open parentheses 2 plus 3 straight i close parentheses open parentheses a plus b straight i close parentheses equals 13

(iii)
open parentheses a plus straight i close parentheses open parentheses 2 plus b straight i close parentheses equals negative 6 plus 22 straight i.

How did you do?

Did this page help you?

7
Sme Calculator7 marks

Consider the complex numbers w equals straight i z and w plus 2 z equals 7 plus 6 straight i.

Find

(i)
Re left parenthesis w right parenthesis

(ii)
Im left parenthesis w right parenthesis

(iii)
Re left parenthesis z right parenthesis

(iv)
Im left parenthesis z right parenthesis.

How did you do?

Did this page help you?

8
Sme Calculator7 marks

It is given that z subscript 1 equals 3 plus 4 straight i and z subscript 2 equals negative 2 plus 2 straight i.

Find

(i)
straight i z subscript 1 plus z subscript 2

(ii)
fraction numerator z subscript 1 over denominator straight i z subscript 2 end fraction

(iii)
straight i left parenthesis z subscript 1 z subscript 2 right parenthesis.

How did you do?

Did this page help you?

9
Sme Calculator8 marks

Find the complex numbers z and w such that 

2 z minus straight i w to the power of asterisk times equals 5 plus 7 straight i 

w plus straight i z to the power of asterisk times equals 5 plus 16 straight i

How did you do?

Did this page help you?

10a
Sme Calculator5 marks

Let z equals 3 plus 8 straight i and w equals 4 minus 4 straight i.

Find theta, the angle shown on the diagram below.

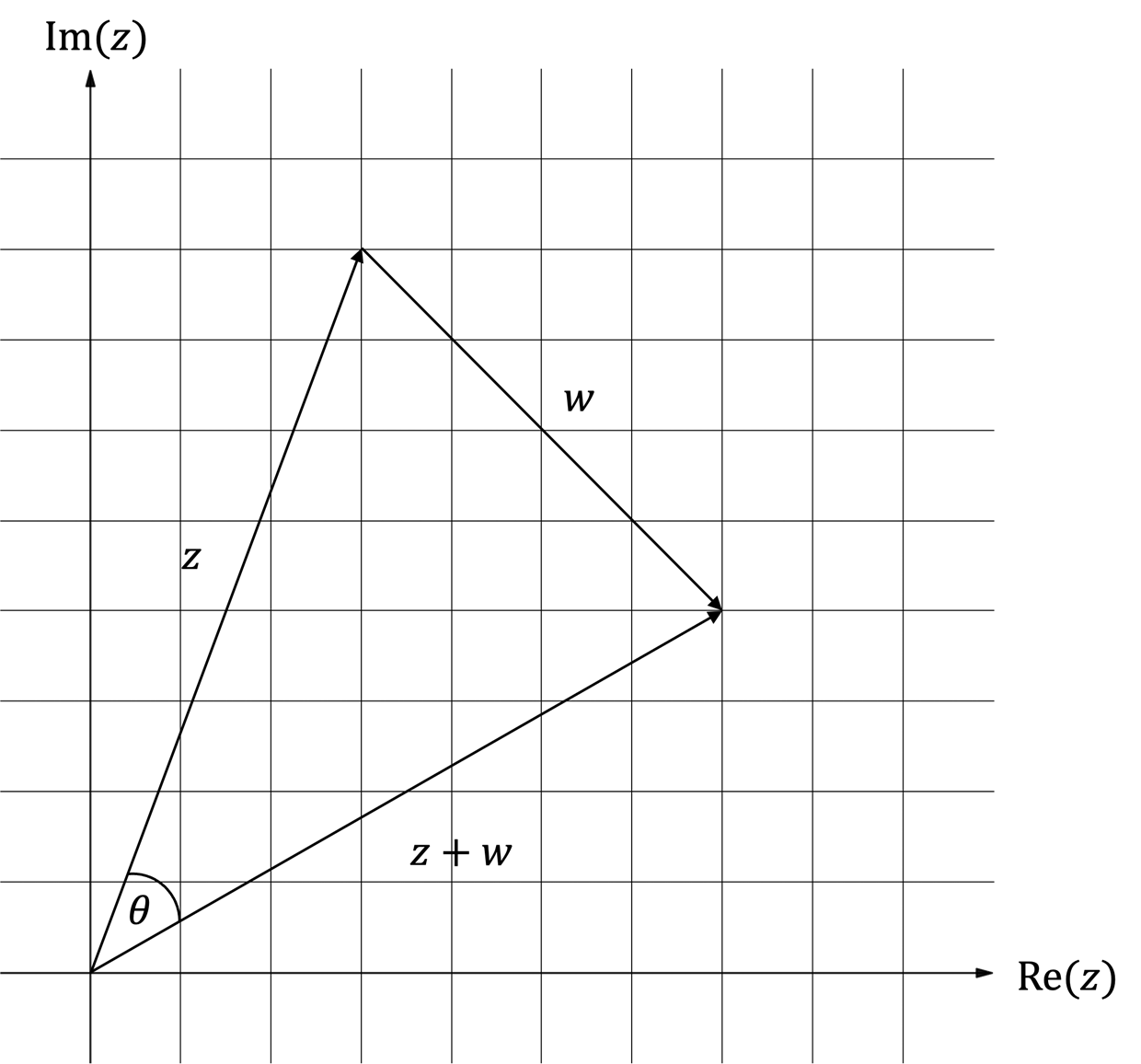
q10a_1-8_complex-numbers_medium_ib-maths-aa-hl

How did you do?

10b
Sme Calculator3 marks

Find the area of the triangle formed in the diagram above.

How did you do?

Did this page help you?

11a
Sme Calculator2 marks

Let z equals negative 1 minus 3 straight i and w equals 1 plus straight i.

Find z w.

How did you do?

11b
Sme Calculator3 marks

Sketch z comma w space and space space z w spaceon the Argand diagram below.

q11b_1-8_complex-numbers_medium_ib-maths-aa-hl

How did you do?

11c
Sme Calculator4 marks

Let theta be the angle between z and z w and ϕ be the angle between w and z w.

Find the angles theta and ϕ, giving your answers in degrees.

How did you do?

Did this page help you?

12a
Sme Calculator4 marks

Let w equals fraction numerator z plus 1 over denominator z to the power of asterisk times plus 1 end fraction, where z equals a plus b straight i comma space a comma space b element of straight real numbers.

Write w in the form x plus y straight i comma space x comma space y element of straight real numbers. space

How did you do?

12b
Sme Calculator3 marks

Determine the conditions under which w is purely imaginary.

How did you do?

Did this page help you?

1a
Sme Calculator3 marks

Consider the quadratic equation z squared minus 8 z plus 25 equals 0 comma space z element of straight complex numbers. 

The roots of the equation are  z subscript 1 equals a plus b straight i  and  z subscript 2 equals a minus b straight i where a comma b element of straight integer numbers. 

Find the value of a and b.

How did you do?

1b
Sme Calculator4 marks

Sketch z subscript 1 comma space z subscript 2 comma space z subscript 1 plus z subscript 2and z subscript 1 minus z subscript 2 on the Argand diagram below, be sure to include an appropriate scale.

q1b-1-8-ib-aa-hl-complex-numbers-hard-maths_dig

How did you do?

Did this page help you?

2
Sme Calculator7 marks

Consider the complex numbers  z subscript 1 equals negative 3 plus 2 straight i and z subscript 2 equals 1 minus 3 straight i.

Find

(i)
z subscript 1 plus z subscript 2
(ii)
z subscript 1 minus z subscript 2
(iii)
z subscript 1 z subscript 2
(iv)
z subscript 1 over z subscript 2

How did you do?

Did this page help you?

3
Sme Calculator7 marks

Consider the complex numbers z subscript 1 equals 3 minus straight i and  z subscript 2 equals negative 2 minus 3 straight i. 

Find the modulus and argument of z subscript 1 z subscript 2 to the power of asterisk times.

How did you do?

Did this page help you?

4a
Sme Calculator6 marks

Consider the complex numbers z subscript 1 equals 1 minus 2 straight i and z subscript 2 equals negative 3 plus 5 straight i.   

Work out the following:

(i)
Re open parentheses straight z subscript 2 minus straight z subscript 1 close parentheses
(ii)
Im open parentheses z subscript 1 z subscript 2 close parentheses
(iii)
open parentheses z subscript 1 over z subscript 2 close parentheses to the power of asterisk times

For part (iii) give your answer in the form a plus b straight i,  where a and b are real numbers.

How did you do?

4b
Sme Calculator2 marks

Write down the complex conjugate of z subscript 2 and describe the geometrical relationship between z subscript 2 and z subscript 2 to the power of asterisk times.

How did you do?

Did this page help you?

5
Sme Calculator7 marks

Find all possible real values for a and b such that

(i)
open parentheses a plus b straight i close parentheses open parentheses 2 minus 3 straight i close parentheses equals 8 plus straight i
(ii)
a open parentheses 2 plus b straight i close parentheses equals b open parentheses negative 6 plus straight i close parentheses
(iii)
open parentheses 2 a plus 3 straight i close parentheses open parentheses 3 plus b straight i close parentheses equals 12 plus 21 straight i

How did you do?

Did this page help you?

6a
Sme Calculator3 marks

For a general complex number z equals x plus straight i y,  where x comma y element of straight real numbers,  show that

(i)
Re open parentheses z close parentheses equals fraction numerator z plus z italic asterisk times over denominator 2 end fraction
(ii)
Im open parentheses z close parentheses equals fraction numerator z minus z to the power of asterisk times over denominator 2 straight i end fraction

 

How did you do?

6b
Sme Calculator6 marks

For the complex numbers z subscript 1 equals a subscript 1 plus b subscript 1 straight i and z subscript 2 equals a subscript 2 plus b subscript 2 straight i,  where  a subscript 1 comma space a subscript 2 comma space b subscript 1 comma space b subscript 2 element of straight real numbers, show that

open vertical bar z subscript 1 z subscript 2 close vertical bar equals open vertical bar z subscript 1 close vertical bar open vertical bar z subscript 2 close vertical bar

How did you do?

Did this page help you?

7
Sme Calculator8 marks

Consider the complex numbers w equals 2 straight i z and w minus z equals 5 minus 5 straight i.

Find

(i)
open vertical bar z close vertical bar
(ii)
arg space w
(iii)
Re open parentheses z plus w close parentheses
(iv)
Im open parentheses z minus w close parentheses

How did you do?

Did this page help you?

8a
Sme Calculator4 marks

Consider the complex numbers z subscript 1 equals a minus 6 straight i comma space straight z subscript 2 equals 1 plus b straight i and z subscript 1 z subscript 2 equals negative 17 minus 9 straight i where a comma space b element of straight real numbers. 

Find the possible values of a and b.

How did you do?

8b
Sme Calculator2 marks

Using the answers gained in part (a), write down values for c and d that will satisfy the equation

negative open parentheses 3 plus straight i close parentheses open parentheses c plus d straight i close parentheses equals 17 minus 9 straight i

How did you do?

Did this page help you?

9a
Sme Calculator2 marks

Consider the complex numbers z equals 3 plus 5 straight i space and space w equals negative 2 plus 3 straight i. 

Represent the complex numbers z and w on an Argand diagram.

How did you do?

9b
Sme Calculator5 marks

The points z plus w and z minus w are represented by the points straight A and straight B on the Argand diagram respectively.

Find the angle straight A straight O with hat on top straight B.

How did you do?

Did this page help you?

10a
Sme Calculator4 marks

Consider the complex numbers z equals negative 4 minus 3 straight i comma space w equals a i and  z over w equals b plus 2 a straight i, where a comma space b element of straight real numbers.

Find the possible values of a and b.

How did you do?

10b
Sme Calculator3 marks

Find the modulus of w over z.

How did you do?

Did this page help you?

11a
Sme Calculator4 marks

Let omega subscript 1 equals 3 minus straight i space and space omega subscript 2 equals 1 plus 2 straight i.

Given that 1 over omega subscript 1 plus 1 over omega subscript 2 equals 1 over z, express z in the form a plus b straight i, where a comma b element of straight real numbers.

How did you do?

11b
Sme Calculator2 marks

Find omega subscript 1 omega subscript 2 z to the power of asterisk times, giving your answer in the form a plus b straight i, where a comma space b element of straight real numbers.

How did you do?

Did this page help you?

1a
Sme Calculator4 marks

Consider the complex numbers z subscript 1 equals square root of 3 plus 2 straight i and z subscript 2 equals straight i minus 3 square root of 3.

Find

(i)
u equals z subscript 1 z subscript 2
(ii)
v equals z subscript 1 over z subscript 2

How did you do?

1b
Sme Calculator3 marks

The complex numbers u and v are represented by the points straight A and straight B respectively on an Argand diagram with origin straight O. 

Determine whether the angle made by OA with the positive horizontal axis is greater than or less than the angle made by OB with the positive horizontal axis. Give a reason for your answer.

How did you do?

Did this page help you?

2a
Sme Calculator4 marks

Consider the complex number z equals negative a plus 3 over 4 straight i.

Write down, in terms of a,

(i)
Re open parentheses z to the power of italic 2 close parentheses
(ii)
Im open parentheses z to the power of italic 3 close parentheses

How did you do?

2b
Sme Calculator4 marks

In the case where a equals 2, find the modulus and argument of z cubed.

How did you do?

Did this page help you?

3a
Sme Calculator3 marks

Consider the complex numbers  z subscript 1 equals straight i minus 1 half and z subscript 2 equals 1 half minus 3 over straight i.

Express z subscript 2 in the form a plus b straight i, where a comma b element of straight real numbers.

How did you do?

3b
Sme Calculator6 marks

Find

(i)
z subscript 1 to the power of asterisk times z subscript 2
(ii)
z subscript 2 over z subscript 1
(iii)
open vertical bar z subscript 2 over z subscript 1 close vertical bar, giving your answer as an exact value.

How did you do?

Did this page help you?

4
Sme Calculator6 marks

Consider a general complex number z equals x plus straight i y,  where  x comma space y element of straight real numbers , z element of straight complex numbers and  z not equal to 0. 

Show that

(i)
Re open parentheses 1 over straight z plus 1 over straight z to the power of asterisk times close parentheses equals fraction numerator 2 x over denominator x to the power of italic 2 plus y to the power of italic 2 end fraction
(ii)
Im open parentheses 1 over z plus 1 over z to the power of italic asterisk times close parentheses equals 0
(iii)
z z to the power of asterisk times equals open vertical bar z close vertical bar squared

How did you do?

Did this page help you?

5a
Sme Calculator4 marks

Consider the equation z w minus w plus straight i z plus 1 equals 0, where w comma space z element of straight complex numbers, w equals x plus straight i y.

Find an expression in terms of x and y for Re open parentheses z close parentheses.

How did you do?

5b
Sme Calculator4 marks

Find in terms of x given that z is purely real.

How did you do?

Did this page help you?

6a
Sme Calculator5 marks

Consider the complex numbers z subscript 1 equals fraction numerator 3 minus straight i over denominator 1 minus 2 straight i end fraction and z subscript 2 equals negative 3 straight i plus 1. 

Find the modulus of z subscript 1 over z subscript 2 to the power of asterisk times   giving your answer as an exact value.

How did you do?

6b
Sme Calculator2 marks

The argument of z subscript 1 over z subscript 2 to the power of asterisk times is given as theta equals tan to the power of negative 1 end exponent x, where 0 less than theta less than 2 straight pi.  Find the value of x.

How did you do?

Did this page help you?

7a
Sme Calculator3 marks

Consider the complex numbers z equals v over w comma v equals 1 minus p i space and space straight w equals 3 straight i minus 2 

Express z in the form a plus b straight i, where a comma space b comma space p element of straight real numbers..

How did you do?

7b
Sme Calculator4 marks

In the case where z is purely imaginary, represent v comma space w and z on an Argand diagram.

How did you do?

Did this page help you?

8a
Sme Calculator4 marks

Consider the complex numbers z equals fraction numerator a minus 3 straight i over denominator 2 plus straight i end fraction comma space w equals a plus b text i end text and z over w equals 1 plus 2 straight i  where a comma space b element of straight real numbers.

Find the values of a  and b.

How did you do?

8b
Sme Calculator2 marks

Find the modulus of w over z, giving your answer as an exact value.

How did you do?

8c
Sme Calculator2 marks

Find the argument of w over z , giving your answer in the range negative straight pi less or equal than arg w over z less or equal than pi  .

How did you do?

Did this page help you?

9
Sme Calculator7 marks

Consider the complex numbers a minus w equals 2 z minus straight i and w minus 2 z equals b straight i minus 1. 

Find the values of a and b such that Re open parentheses w close parentheses equals Im open parentheses z close parentheses and Re open parentheses w close parentheses equals Re open parentheses z close parentheses plus 1.

How did you do?

Did this page help you?

10a
Sme Calculator3 marks

Consider the complex numbers z subscript 1 equals 5 plus p straight i, z subscript 2 equals a plus b straight i and z subscript 1 over z subscript 2 equals negative 1 plus straight i , where z element of straight complex numbers
and a comma space b element of straight real numbers.

Find the values of a and b in terms of p. 

How did you do?

10b
Sme Calculator3 marks

Given that open vertical bar z subscript 2 close vertical bar equals square root of 73 , find the possible values of p.

How did you do?

10c
Sme Calculator2 marks

Given additionally that arg open parentheses z subscript 2 close parentheses equals 2.78  radians correct to 2 decimal places, determine the exact value of Im open parentheses z subscript 2 close parentheses .

How did you do?

Did this page help you?