Permutations & Combinations (DP IB Maths: AA HL)

A scientist is randomly writing out permutations of the 5 letters and the 2 numbers in the acronym COVID 19.

Find the number of different arrangements of the seven characters that could be created if

If only the five letters are used, find the number of possible arrangements if (reading from left to right) the letter D must be in a position after the letter C.

The scientist arranges the five letters and two numbers so that they make up the seven vertices of a regular heptagon, and then uses straight lines to join each vertex of the heptagon to each other vertex. Use counting principles to explain why there are exactly 21 lines.

Consider two parallel lines A and B.  Line A has 7 distinct points marked on it and line B has 4 distinct points marked on it.  The diagram below shows one possible example of this:

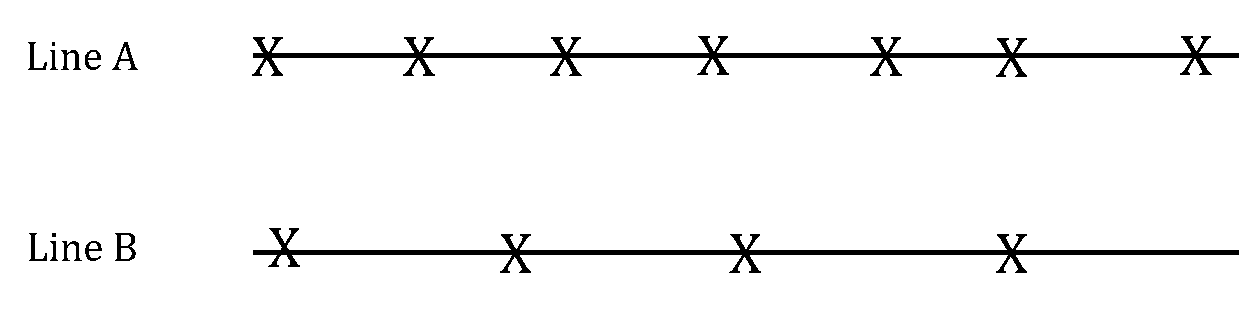
New lines are now drawn between the two parallel lines, so that each marked point on line A is joined to each marked point on line B by exactly one new line. 

Determine the maximum number of points of intersection between the newly constructed lines.

Explain why the answer to part (a) is a maximum.

Consider the letters of the word ALGORITHM. Find the number of permutations of three letters that can be chosen if

Consider the nine letters in the word MAGNITUDE.

Find the number of ways that the nine letters may be arranged if

Find the probability that if the nine letters in the word MAGNITUDE are arranged randomly, none of the vowels will be next to each other.

A mixed relay team must consist of four competitors, two of whom must be male and two of whom must be female.  There are nine men and six women trying out for a place on a new team. 

During the try-outs the fifteen candidates are split into three groups of four and one group of three. Find the number of ways this could be done if the candidates are divided randomly.

Two of the candidates are brother and sister and have agreed that they will only be in the final relay team if they are both successful. Find how many ways the final relay team can be chosen if the brother and sister are either both in or both out.

An examination paper consists of four questions in section A and eight questions in section B.  Candidates must answer five questions from the paper in any order. 

Find the number of ways a candidate can choose their questions if

Candidates are now told that if they choose question 1 from section A they cannot choose any other question from section A. However if they do not choose question 1 from section A then they must choose at least two questions from section A and answer question 1 from section B.  Find the number of ways a candidate could choose their questions under these restrictions.

Dylan is preparing a playlist for his friend’s birthday party.  Dylan chooses 5 different afrobeats songs, 3 different blues song, 3 different country songs and 8 different drum and bass songs.  

Find the number of different orders Dylan can play the songs in if

Whilst at the party a friend likes Dylan’s music and decides to use it to make a playlist of her own.  The friend only has space for twelve songs on her computer.  Find the number of ways Dylan’s friend can choose and arrange twelve out of the nineteen songs if she decide to have two blues songs first, followed by alternating afrobeats and drum and bass songs

In his classroom Mr Roland has seven different books about GeoGebra, five different books about football, and three different Mathematics textbooks. 

Find how many ways Mr Roland could organise the books on his bookshelf if

   Give your answers in the form .where  and .

Mr Roland’s young son selects three of the books at random to sit on whilst doing his homework. Find the number of possible different selections from the fifteen books that there are if

Consider ten cards numbered 1, 2, 3, 4, 5, 6, 7, 8, 9 and 0. 

The ten cards are placed randomly in a line. Find how many ways this can be done if

(iii)

the number formed by the ten cards is greater than .

Four of the ten cards are chosen at random and placed in a line to make a 4-digit code. Find the number of possible codes that can be made if the code is required to be an even number.

Helen is researching three different types of tree as part of her IB Biology Internal Assessment.  She has collected samples from four different acacia trees, two different banyan trees and three different cedar trees.  She needs to choose six of the tree samples to include in her final write up.

Find the number of different selections of the tree samples that could be made if she must have at least one cedar tree sample but cannot include more than three samples of any single type.

Helen chooses three acacia samples, two banyan samples and one cedar sample to include in her final write up. 

Find the number of different orders in which she can arrange these samples in a row if the two banyan samples must not be next to each other.

Consider a circular clock with the numbers 1 through 12 spaced evenly around the outside of the clock face. 

Lines are drawn connecting each of the 12 numbers with each of the other numbers.

Find the number of lines that

Consider the triangles formed on the face of the clock by groups of three of the of the above lines, where the vertices of each triangle lie at three distinct numbers on the clock face.  For example, the lines from 12 to 4, and 4 to 7, and 7 to 12 will form one of these triangles. 

Find the number of triangles that

A horse-riding club uses 8 small fields arranged in two rows of four to allow its horses to graze.

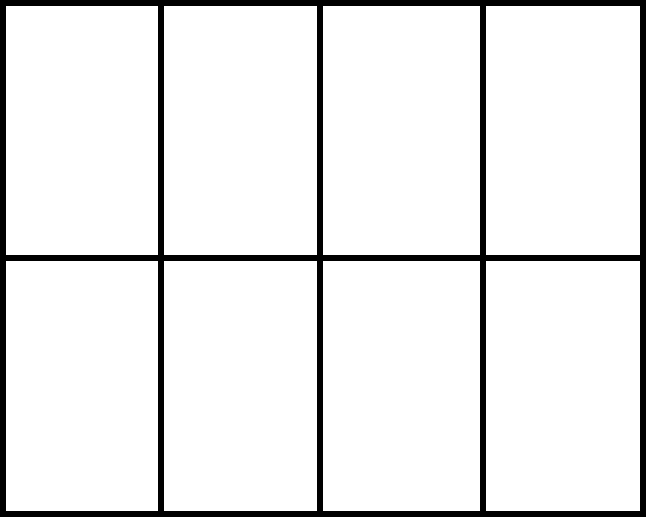
The riding club has 8 horses in total, but three of the horses – named Angel, Blue and Chance – get agitated if they are placed too close to each other for too long. 

For each of the following sets of conditions, find the number of possible ways of placing the 8 horses in the 8 fields. 

Each field may contain up to 6 horses. Angel, Blue and Chance, however, must each be in a separate field.

Each field may contain at most one horse. Additionally Angel must be in one of the corner fields, and Angel, Blue and Chance must not be placed in fields which share any boundaries (it is okay if the fields meet at a corner, but they may not share a side).

Consider the ten letters in the word QUARANTINE. 

Find the number of ways that four letters can be chosen at random from the word QUARANTINE if the selection may contain

Find the number of distinct ways four out of the ten letters of the word QUARANTINE can be arranged if in each case all four letters are different from each other.

Consider the eight letters in the word CAMPFIRE. 

Find the number of ways in which the eight letters may be arranged if

Find the number of ways in which the eight letters in the word CAMPFIRE may be arranged, given that at least two of the vowels must be next to each other

Ahmed is playing a game with the following nine cards:

Ahmed arranges the cards to form a 9-digit number. Find how many different 9-digit numbers can be made such that the number is a multiple of five and the circular cards are not all together.

Ahmed chooses one triangular card, one circular card and one rectangular card at random and arranges them to make a 3-digit code. Find the number of different 3-digit codes Ahmed could make.

Jonni always struggles to decide which combination of fillings, sides and sauces he wants to put in his sandwich at his favourite sandwich shop. The available options are listed below: 

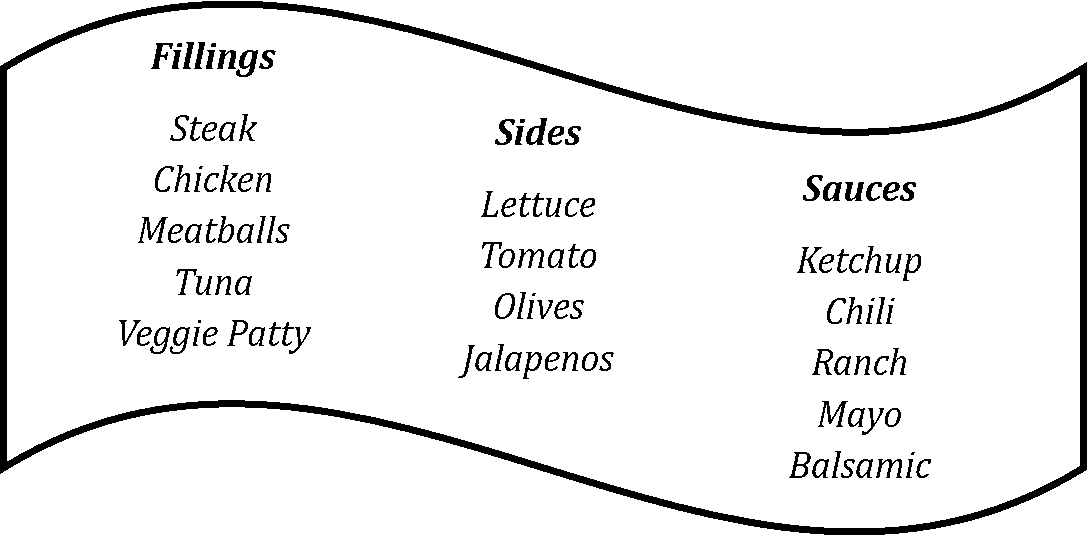
To avoid having to make up his mind, each day Jonni instead sets himself a rule for how many of each option he will put in his sandwich, and then uses an app he has designed to choose one sandwich at random from among those that his rule allows.  Note that choosing the same filling, side or sauce more than once is never allowed.

If Jonni’s rule on a given day is that he will have one filling, three sides and one type of sauce in his sandwich, find the probability that Jonni has either steak or chicken in his sandwich.

If Jonni’s rule on a given day is that he will have two fillings, one side and three types of sauce in his sandwich, find the probability that he gets either tuna with tomato, or jalapenos with ketchup and mayo, as a part of his sandwich choice.

Twenty-six people are travelling on an airplane. Seven of them are businesspeople on their way to a facilities management conference. Three of them are spies on their way to take up positions as ‘consular officials’ in an unnamed embassy. The other sixteen are cryptozoologists on their way to follow up some clues regarding a recent unicorn sighting. These passengers have been randomly allocated the seats from 26A to 29E inclusive, as depicted in the diagram below. 

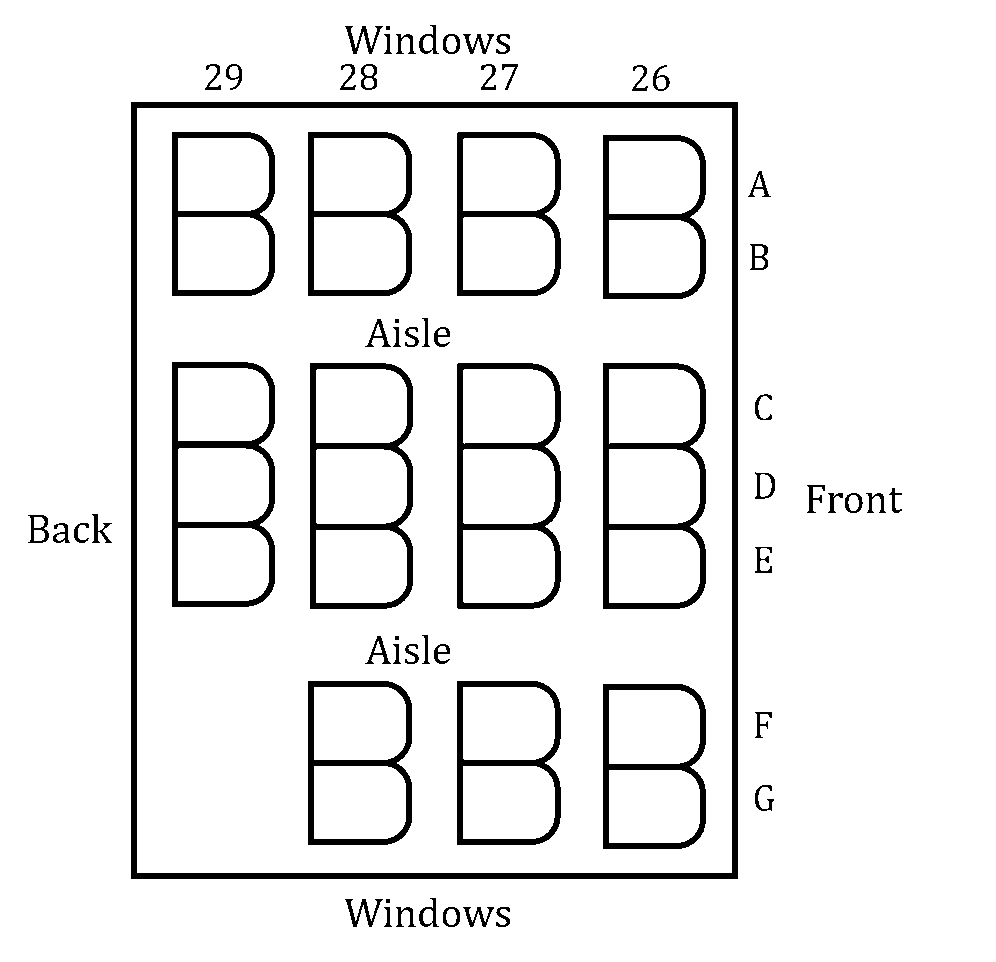
Find the number of ways that all twenty-six people could be seated on the plane if the three spies are all sat in the back row and the seven businesspeople are all in seats by a window.

Given that each of the seven window seats has a cryptozoologist in it, find the probability that the three spies are not all sat together in one of the groups of three seats in between the two aisles.

The following four family groups, consisting of 6 adults and 12 children in total, are all going to the cinema together: 

• Mr and Mrs Mitchell and their two children 

• Mrs and Mrs Lee and their four children 

• Mr Kim and his three children 

• Ms Miller and her three children 

Find the number of different ways that all 18 people can sit in a row of 18 seats if

If instead the 18 people are sat randomly in three rows of six, what is the probability that all of the adults will be sat in the back row?

The diagram below shows part of a train carriage. There are twenty-eight seats consisting of twenty normal seats, S, and eight table seats, T. In this part of the train carriage there is a group of twelve schoolchildren and two teachers, along with a married couple, four businessmen, and three backpackers.

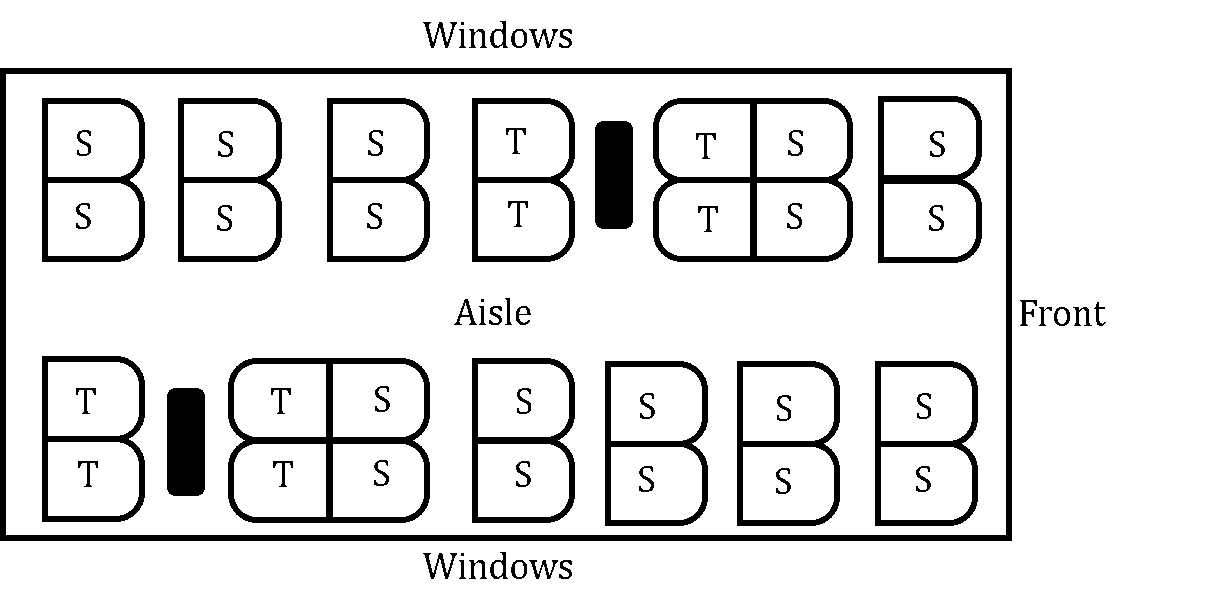
Find the number of ways that the passengers could be arranged in this part of the train carriage if

Given that everybody is arranged completely at random within this part of the train carriage, find the probability that

A total of n tasks are to be shared among m people, where each of the people is uniquely identified by a number between 1 and .  Person 1 is to receive  tasks, Person 2 is to receive  tasks, and so on, with the integers  being such that        and . 

Show that the number of different ways in which the tasks can be assigned according to the above rules is