Consider the letters of the word SUNDAY. Find the number of permutations of four letters that can be chosen if
Did this page help you?
Select a download format for 1.7 Permutations & Combinations
Consider the letters of the word SUNDAY. Find the number of permutations of four letters that can be chosen if
How did you do?
Did this page help you?
Three letters are chosen at random from the letters in the word AIRFIELD.
Find the number of ways that the selection may contain
How did you do?
Write down the number of arrangements of three letters chosen at random from the word AIRFIELD that have exactly one letter I.
How did you do?
Did this page help you?
In a maths test students are required to answer four out of seven questions.
Find the number of ways in which the questions can be chosen if there are no restrictions.
How did you do?
Find the number of ways in which the questions can be chosen if the last question is compulsory.
How did you do?
Find the number of ways in which the questions can be chosen if the students must do at least 1 of the last two questions.
How did you do?
Did this page help you?
A farm has a new litter of kittens. Two of the kittens are classed as mostly white, four are mostly black, and five are classed as black and white mixed.
Five of the kittens are selected at random.
Find the number of ways in which the selection might contain:
How did you do?
Find the number of ways in which the selection might contain at least two kittens that are classed as mostly black.
How did you do?
Did this page help you?
A pool table has fifteen different balls including the black ball.
Given that the black ball is the last to be potted and the rest of the balls are potted one at a time in a random order, in how many ways can the fifteen balls be potted?
How did you do?
The other fourteen balls consist of seven pairs of different coloured balls. One of each pair has a stripe across it and the other has a spot on it.
Given that the black ball is still the last to be potted, in how many ways can the fifteen balls be potted one at a time if
How did you do?
Did this page help you?
Ms Aiba has twelve different maths textbooks on her classroom bookshelf. Five of them are Statistics textbooks and the other seven are Pure Mathematics textbooks. Determine the number of different ways that the books can be arranged on the shelf if
How did you do?
Did this page help you?
Nine shirts for a baseball team are numbered from 1 to 9. Five players are allowed to take one shirt each.
Find the number of ways this can be done if
How did you do?
Did this page help you?
Riley is going on holiday and is allowed to bring along four of his toys. At home he has nine different plastic dinosaurs, six different toy cars, and five different wooden reptiles.
How many different selections of his toys can he make if he chooses at least one of each type of toy?
How did you do?
Riley can’t decide so he persuades his parents to allow him to bring along five toys instead.
Given that he brings more plastic dinosaurs than any other type of toy, how many different selections can he make now?
How did you do?
Did this page help you?
Two parents, Julie and Malcolm, have 15 household chores to be given to their five children, Biddy, Gus, Mandy, Charlie and Claire.
Find the number of ways in which the 15 household chores can be distributed if Biddy is to do 5 of them, Gus is to do 4 of them, Mandy is to do 3 of them, Charlie is to do 2 of them and Claire is to 1 of them.
How did you do?
Did this page help you?
A team of 16 is to be split up in order to complete a number of tasks.
Find the number of ways the team can be divided into
How did you do?
A quarter of the team are unable to help with the tasks due to COVID-19 infections.
Find the number of ways that the remaining team members can be divided into
How did you do?
Did this page help you?
You have a set of four different coloured flashlights that you use to send messages to your friend who lives across from you on the same street.
(For purposes of this question, a ‘message’ is considered to be a single sequence of one or more coloured lights, displayed one after the other.)
Find the number of different messages you can send using two different coloured flashlights displayed one after the other.
How did you do?
Find the number of different messages you can send using three different coloured flashlights displayed one after the other.
How did you do?
Find the total number of different messages you could send using your four flashlights, under the condition that all the colours in a given message must be different from each other.
How did you do?
Did this page help you?
In this question give your answers in the form , where
and
John is a builder who has divided his day’s work into 15 separate tasks. Two of these tasks John considers ‘physically demanding’ because one includes moving bricks and the other includes concrete mixing.
Find the number of ways John can complete the tasks given that one ‘physically demanding’ task is done at the start of the day and the other ‘physically demanding’ task is done at the end of the day.
How did you do?
Find the number of ways John can complete the tasks given that the two physically demanding tasks are not done consecutively.
How did you do?
Did this page help you?
A scientist is randomly writing out permutations of the 5 letters and the 2 numbers in the acronym COVID 19.
Find the number of different arrangements of the seven characters that could be created if
How did you do?
If only the five letters are used, find the number of possible arrangements if (reading from left to right) the letter D must be in a position after the letter C.
How did you do?
The scientist arranges the five letters and two numbers so that they make up the seven vertices of a regular heptagon, and then uses straight lines to join each vertex of the heptagon to each other vertex. Use counting principles to explain why there are exactly 21 lines.
How did you do?
Did this page help you?
Consider two parallel lines A and B. Line A has 7 distinct points marked on it and line B has 4 distinct points marked on it. The diagram below shows one possible example of this:
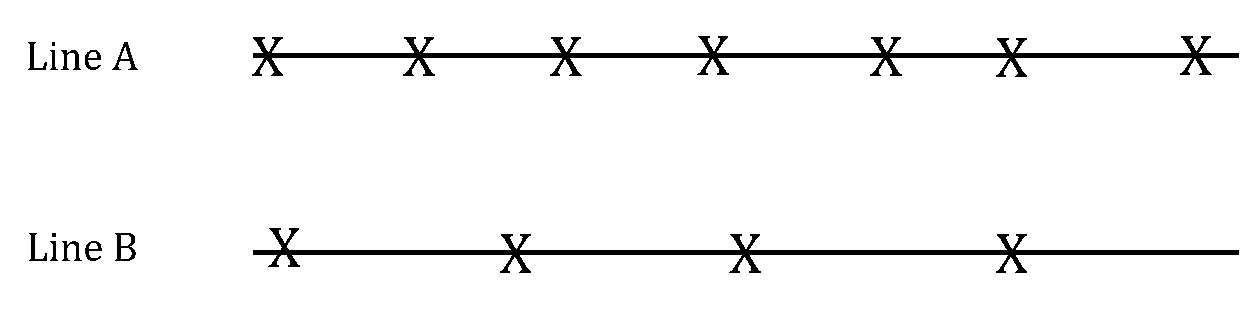
New lines are now drawn between the two parallel lines, so that each marked point on line A is joined to each marked point on line B by exactly one new line.
Determine the maximum number of points of intersection between the newly constructed lines.
How did you do?
Explain why the answer to part (a) is a maximum.
How did you do?
Did this page help you?
Consider the letters of the word ALGORITHM. Find the number of permutations of three letters that can be chosen if
How did you do?
Did this page help you?
Consider the nine letters in the word MAGNITUDE.
Find the number of ways that the nine letters may be arranged if
How did you do?
Find the probability that if the nine letters in the word MAGNITUDE are arranged randomly, none of the vowels will be next to each other.
How did you do?
Did this page help you?
A mixed relay team must consist of four competitors, two of whom must be male and two of whom must be female. There are nine men and six women trying out for a place on a new team.
During the try-outs the fifteen candidates are split into three groups of four and one group of three. Find the number of ways this could be done if the candidates are divided randomly.
How did you do?
Two of the candidates are brother and sister and have agreed that they will only be in the final relay team if they are both successful. Find how many ways the final relay team can be chosen if the brother and sister are either both in or both out.
How did you do?
Did this page help you?
An examination paper consists of four questions in section A and eight questions in section B. Candidates must answer five questions from the paper in any order.
Find the number of ways a candidate can choose their questions if
How did you do?
Candidates are now told that if they choose question 1 from section A they cannot choose any other question from section A. However if they do not choose question 1 from section A then they must choose at least two questions from section A and answer question 1 from section B. Find the number of ways a candidate could choose their questions under these restrictions.
How did you do?
Did this page help you?
Dylan is preparing a playlist for his friend’s birthday party. Dylan chooses 5 different afrobeats songs, 3 different blues song, 3 different country songs and 8 different drum and bass songs.
Find the number of different orders Dylan can play the songs in if
How did you do?
Whilst at the party a friend likes Dylan’s music and decides to use it to make a playlist of her own. The friend only has space for twelve songs on her computer. Find the number of ways Dylan’s friend can choose and arrange twelve out of the nineteen songs if she decide to have two blues songs first, followed by alternating afrobeats and drum and bass songs
How did you do?
Did this page help you?
In his classroom Mr Roland has seven different books about GeoGebra, five different books about football, and three different Mathematics textbooks.
Find how many ways Mr Roland could organise the books on his bookshelf if
Give your answers in the form .where
and
.
How did you do?
Mr Roland’s young son selects three of the books at random to sit on whilst doing his homework. Find the number of possible different selections from the fifteen books that there are if
How did you do?
Did this page help you?
Consider ten cards numbered 1, 2, 3, 4, 5, 6, 7, 8, 9 and 0.
The ten cards are placed randomly in a line. Find how many ways this can be done if
How did you do?
Four of the ten cards are chosen at random and placed in a line to make a 4-digit code. Find the number of possible codes that can be made if the code is required to be an even number.
How did you do?
Did this page help you?
Helen is researching three different types of tree as part of her IB Biology Internal Assessment. She has collected samples from four different acacia trees, two different banyan trees and three different cedar trees. She needs to choose six of the tree samples to include in her final write up.
Find the number of different selections of the tree samples that could be made if she must have at least one cedar tree sample but cannot include more than three samples of any single type.
How did you do?
Helen chooses three acacia samples, two banyan samples and one cedar sample to include in her final write up.
Find the number of different orders in which she can arrange these samples in a row if the two banyan samples must not be next to each other.
How did you do?
Did this page help you?
Consider a circular clock with the numbers 1 through 12 spaced evenly around the outside of the clock face.
Lines are drawn connecting each of the 12 numbers with each of the other numbers.
Find the number of lines that
How did you do?
Consider the triangles formed on the face of the clock by groups of three of the of the above lines, where the vertices of each triangle lie at three distinct numbers on the clock face. For example, the lines from 12 to 4, and 4 to 7, and 7 to 12 will form one of these triangles.
Find the number of triangles that
How did you do?
Did this page help you?
A horse-riding club uses 8 small fields arranged in two rows of four to allow its horses to graze.
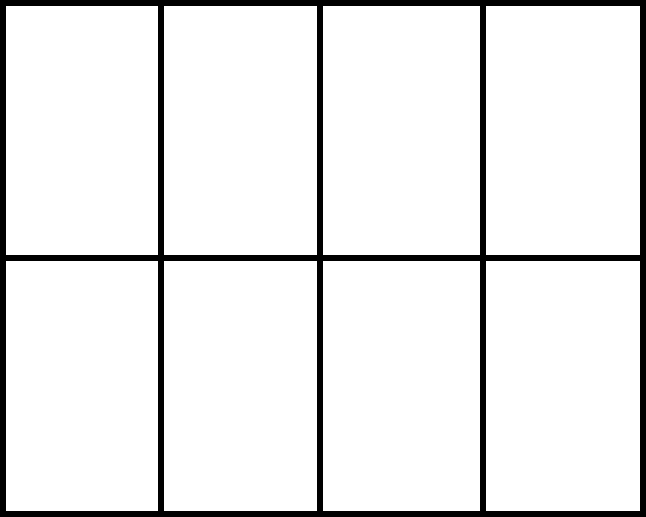
The riding club has 8 horses in total, but three of the horses – named Angel, Blue and Chance – get agitated if they are placed too close to each other for too long.
For each of the following sets of conditions, find the number of possible ways of placing the 8 horses in the 8 fields.
Each field may contain up to 6 horses. Angel, Blue and Chance, however, must each be in a separate field.
How did you do?
Each field may contain at most one horse. Additionally Angel must be in one of the corner fields, and Angel, Blue and Chance must not be placed in fields which share any boundaries (it is okay if the fields meet at a corner, but they may not share a side).
How did you do?
Did this page help you?
Consider the ten letters in the word QUARANTINE.
Find the number of ways that four letters can be chosen at random from the word QUARANTINE if the selection may contain
How did you do?
Find the number of distinct ways four out of the ten letters of the word QUARANTINE can be arranged if in each case all four letters are different from each other.
How did you do?
Did this page help you?
Consider the eight letters in the word CAMPFIRE.
Find the number of ways in which the eight letters may be arranged if
How did you do?
Find the number of ways in which the eight letters in the word CAMPFIRE may be arranged, given that at least two of the vowels must be next to each other
How did you do?
Did this page help you?
Ahmed is playing a game with the following nine cards:

Ahmed arranges the cards to form a 9-digit number. Find how many different 9-digit numbers can be made such that the number is a multiple of five and the circular cards are not all together.
How did you do?
Ahmed chooses one triangular card, one circular card and one rectangular card at random and arranges them to make a 3-digit code. Find the number of different 3-digit codes Ahmed could make.
How did you do?
Did this page help you?
Jonni always struggles to decide which combination of fillings, sides and sauces he wants to put in his sandwich at his favourite sandwich shop. The available options are listed below:
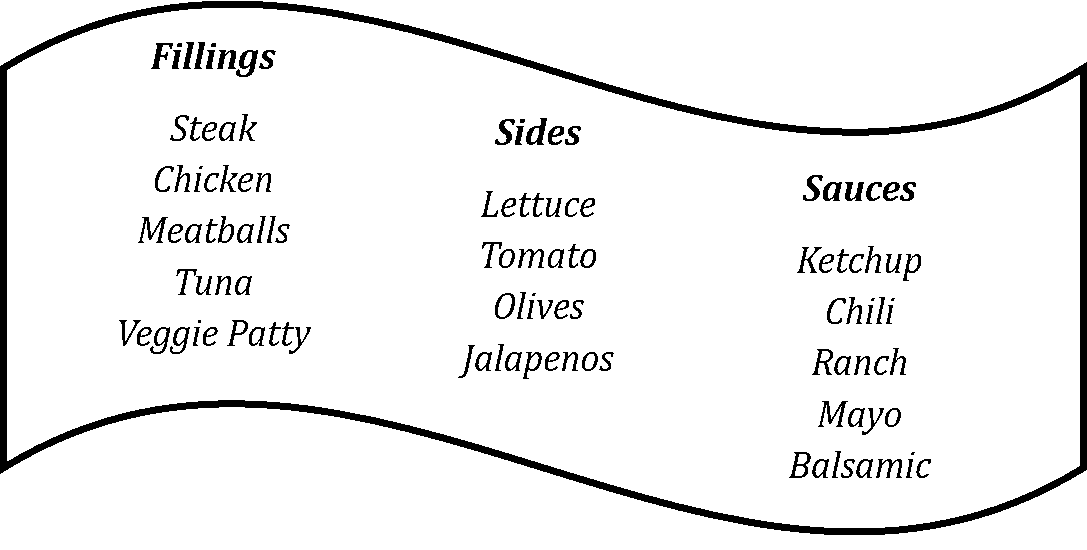
To avoid having to make up his mind, each day Jonni instead sets himself a rule for how many of each option he will put in his sandwich, and then uses an app he has designed to choose one sandwich at random from among those that his rule allows. Note that choosing the same filling, side or sauce more than once is never allowed.
If Jonni’s rule on a given day is that he will have one filling, three sides and one type of sauce in his sandwich, find the probability that Jonni has either steak or chicken in his sandwich.
How did you do?
If Jonni’s rule on a given day is that he will have two fillings, one side and three types of sauce in his sandwich, find the probability that he gets either tuna with tomato, or jalapenos with ketchup and mayo, as a part of his sandwich choice.
How did you do?
Did this page help you?
Twenty-six people are travelling on an airplane. Seven of them are businesspeople on their way to a facilities management conference. Three of them are spies on their way to take up positions as ‘consular officials’ in an unnamed embassy. The other sixteen are cryptozoologists on their way to follow up some clues regarding a recent unicorn sighting. These passengers have been randomly allocated the seats from 26A to 29E inclusive, as depicted in the diagram below.
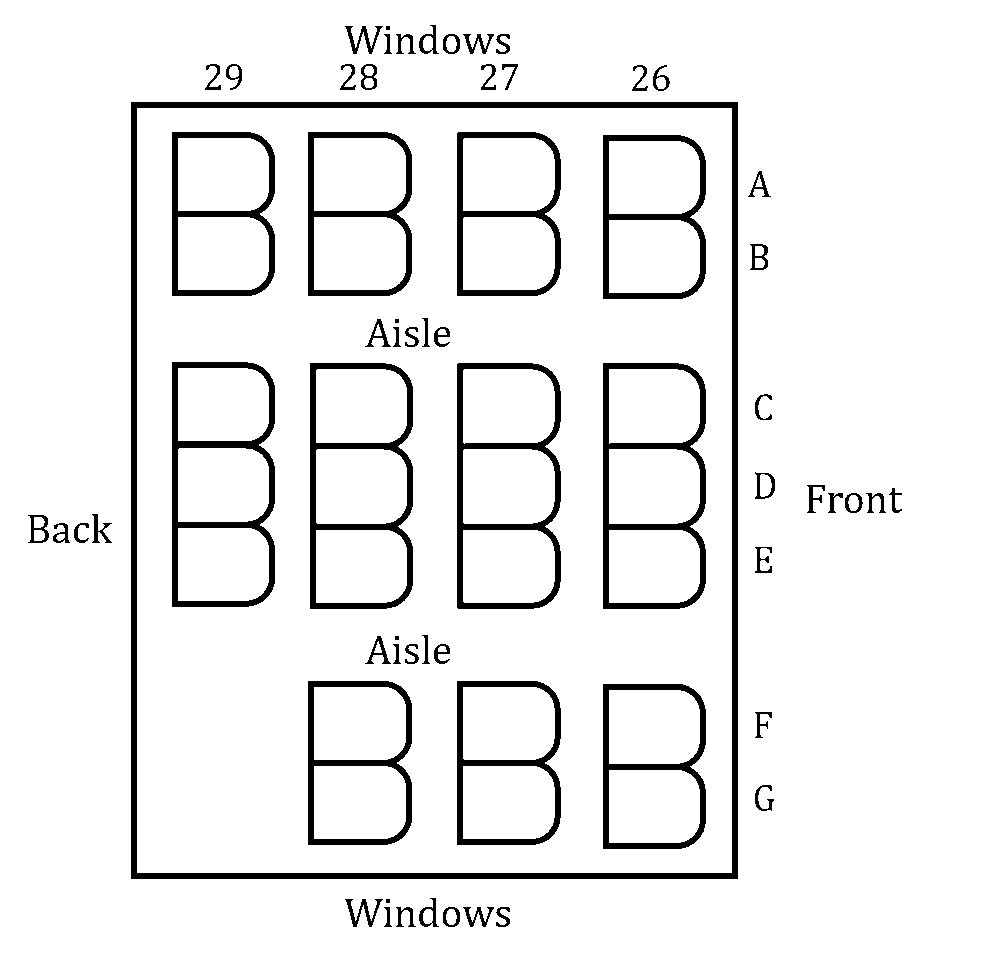
Find the number of ways that all twenty-six people could be seated on the plane if the three spies are all sat in the back row and the seven businesspeople are all in seats by a window.
How did you do?
Given that each of the seven window seats has a cryptozoologist in it, find the probability that the three spies are not all sat together in one of the groups of three seats in between the two aisles.
How did you do?
Did this page help you?
The following four family groups, consisting of 6 adults and 12 children in total, are all going to the cinema together:
Find the number of different ways that all 18 people can sit in a row of 18 seats if
How did you do?
If instead the 18 people are sat randomly in three rows of six, what is the probability that all of the adults will be sat in the back row?
How did you do?
Did this page help you?
The diagram below shows part of a train carriage. There are twenty-eight seats consisting of twenty normal seats, S, and eight table seats, T. In this part of the train carriage there is a group of twelve schoolchildren and two teachers, along with a married couple, four businessmen, and three backpackers.
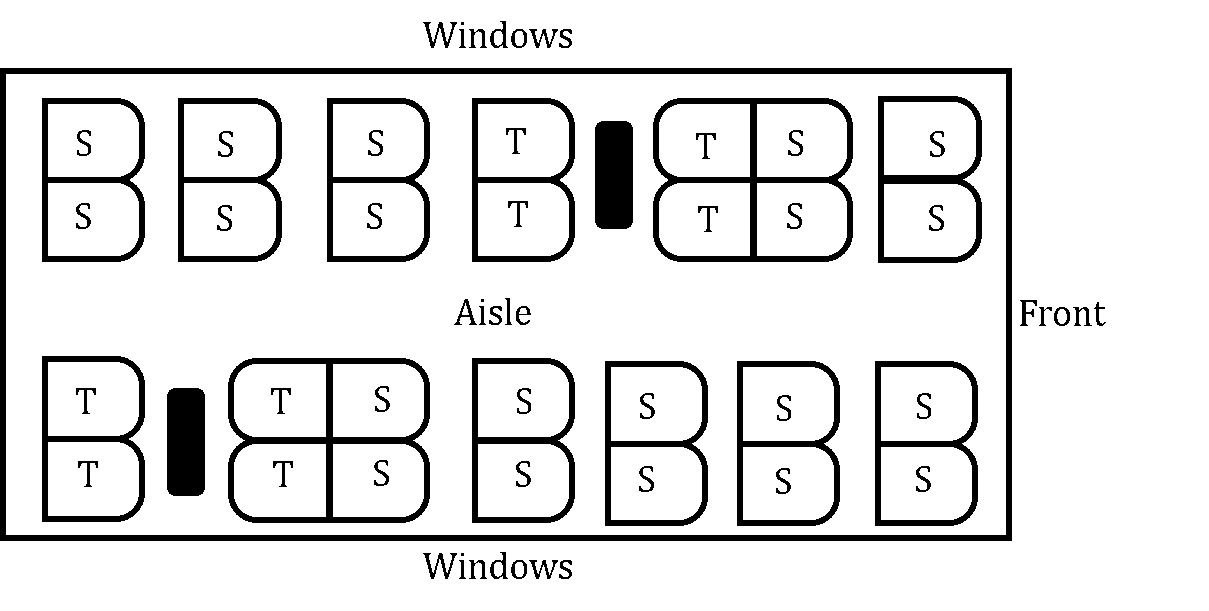
Find the number of ways that the passengers could be arranged in this part of the train carriage if
How did you do?
Given that everybody is arranged completely at random within this part of the train carriage, find the probability that
How did you do?
Did this page help you?
A total of n tasks are to be shared among m people, where each of the people is uniquely identified by a number between 1 and . Person 1 is to receive
tasks, Person 2 is to receive
tasks, and so on, with the integers
being such that
and
.
Show that the number of different ways in which the tasks can be assigned according to the above rules is
How did you do?
Did this page help you?