Implicit Differentiation (DP IB Analysis & Approaches (AA)): Revision Note
Did this video help you?
Implicit differentiation
What is implicit differentiation?
It is not always easy or possible to write an equation connecting x and y explicitly in the form
or
In such cases the equation is written implicitly
as a function of
and
e.g. in the form
The parts of such equations involving
can be differentiated implicitly using the chain rule
A shortcut way of thinking about this is that ‘
is (implicitly) a function of
’
And when differentiating a function of
chain rule says “differentiate with respect to
, then multiply by the derivative of
” (which is
)
How do I find a derivative using implicit differentiation?
In order to find
for an implicit relation between
and
, follow these steps
STEP 1
Differentiate both sides of the equation implicitly with respect to
Usefor terms containing
E.g.
STEP 2
Rearrange the new equation to makethe subject
Examiner Tips and Tricks
In more complicated implicit differentiation questions, you may need to combine other differentiation techniques (e.g. chain rule, product rule, quotient rule) with the implicit differentiation chain rule formula.
Applications of implicit differentiation
What type of problems could involve implicit differentiation?
Broadly speaking there are three types of problem that could involve implicit differentiation
Algebraic problems involving graphs, derivatives, tangents, normals, etc.,
where it is not practical to write
explicitly in terms of
Usually in such cases,
will be in terms of
and
Optimisation problems that involve time derivatives
More than one variable may be involved too
e.g. Volume of a cylinder,
e.g. The side length and (therefore) area of a square increase over time
Any problem that involves differentiating with respect to an extraneous variable
e.g.
but the derivative
is required (rather than
)
How do I apply implicit differentiation to algebraic problems?
Algebraic problems revolve around values of the derivative (gradient)
Particular problems focus on special case tangent values
Horizontal tangents
Also referred to as tangents parallel to the
-axis
This is when
Vertical tangents
Also referred to as tangents parallel to the
-axis
This is when
Recall the relation
Other problems may involve finding equations of (other) tangents and/or normals
For problems that involve finding the coordinates of points on a curve with a specified gradient the method below can be used
STEP 1
Differentiate the equation of the curve implicitly
STEP 2
Substitute the given or implied value ofto create an equation linking
and
STEP 3
There are now two equationsthe original equation
the linking equation
Solve them simultaneously to find the
and
coordinates as required
Examiner Tips and Tricks
After rearranging following implicit differentiation, will often be in terms of both
and
. Unless specifically asked for in the question, there is usually no need to try to write
in terms of
(or
) only.
If evaluating derivatives, you'll need both and
coordinates, so one may have to be found from the other using the original equation.
Worked Example
The curve C has equation .
a) Find the exact coordinates of the points where the normal to curve C has gradient 2.
Answer:

b) Find the equations of the tangents to the curve that are
(i) parallel to the x-axis
(ii) parallel to the y-axis.
Answer:

How do I apply implicit differentiation to optimisation problems?
For a single variable use chain rule to differentiate implicitly
e.g. A square with side length changing over time,
Differentiating both sides with respect to
gives
For more than one variable use product rule (and chain rule) to differentiate implicitly
e.g. A square-based pyramid with base length
and height
changing over time,
Differentiating both sides with respect to
gives
After differentiating implicitly the rest of the question should be similar to any other optimisation problem
Be aware of phrasing
“the rate of change of the height of the pyramid” (over time) is
When finding the location of minimum and maximum problems
The solution is not necessarily at a turning point
The minimum or maximum could be at the start or end of a given or appropriate interval
Examiner Tips and Tricks
If you are struggling to tell which derivative is needed for a question, writing all possibilities down may help you. You don't need to work them out at this stage but if you consider them it may nudge you to the next stage of the solution.
For example, for , possible derivatives are
and
.
Worked Example
The radius, cm, and height,
cm, of a cylinder are increasing with time. The volume,
cm3, of the cylinder at time
seconds is given by
.
a) Find an expression for .
Answer:
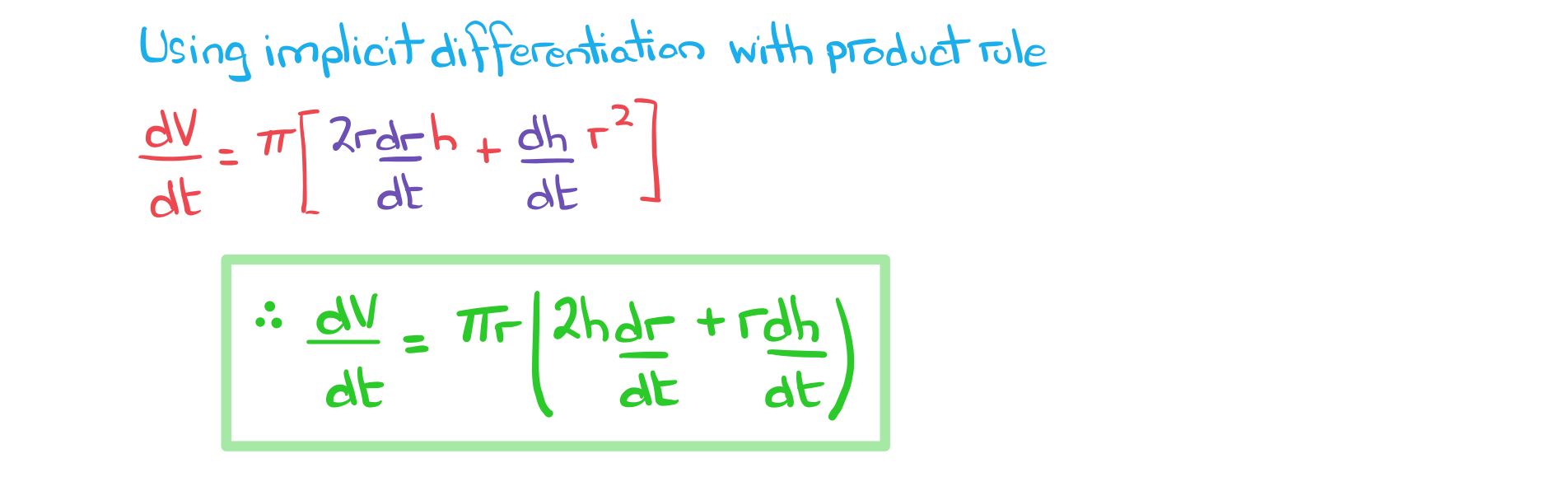
b) At time seconds, the radius of the cylinder is 4 cm, expanding at a rate of 2 cm s-1. At the same time, the height of the cylinder is 10 cm, expanding at a rate of 3 cm s-1.
Find the rate at which the volume is expanding at time seconds.
Answer:


Unlock more, it's free!
Did this page help you?