Introduction to Integration

Did this video help you?

Integration is the opposite to differentiation
- Integration is referred to as antidifferentiation
- The result of integration is referred to as the antiderivative
Integration is the process of finding the expression of a function (antiderivative) from an expression of the derivative (gradient function)

$\int f (x) d x$

- the large operator $\int$ means “integrate”
- “ $d x$ ” indicates which variable to integrate with respect to
- $f (x)$ is the function to be integrated (sometimes called the integrand)
The antiderivative is sometimes denoted by $F (x)$
- there’s then no need to keep writing the whole integral; refer to it as $F (x)$
$F (x)$ may also be called the indefinite integral of $f (x)$

Recall one of the special cases from Differentiating Powers of x
- If $f (x) = a$ then $f' (x) = 0$
This means that integrating 0 will produce a constant term in the antiderivative
- a zero term wouldn’t be written as part of a function
- every function, when integrated, potentially has a constant term
This is called the constant of integration and is usually denoted by the letter $c$
- it is often referred to as “plus $c$ ”
Without more information it is impossible to deduce the value of this constant
- there are endless antiderivatives, $F (x)$ , for a function $f (x)$

Did this video help you?

Integrating Powers of x

Powers of $x$ are integrated according to the following formulae:
- If $f (x) = x^{n}$ then $\int f (x) d x = \frac{x^{n + 1}}{n + 1} + c$ where $n \in ℚ, n \neq - 1$ and $c$ is the constant of integration

If the power of $x$ is multiplied by a constant then the integral is also multiplied by that constant
- If $f (x) = a x^{n}$ then $\int f (x) d x = \frac{a x^{n + 1}}{n + 1} + c$ where $n \in ℚ, n \neq - 1$ and $a$ is a constant and $c$ is the constant of integration
$\frac{d y}{d x}$ notation can still be used with integration
Note that the formulae above do not apply when $n = - 1$ as this would lead to division by zero
Remember the special case:
- $\int a d x = a x + c$
  - e.g. $\int 4 d x = 4 x + c$
- This allows constant terms to be integrated
Functions involving roots will need to be rewritten as fractional powers of $x$ first
- eg. If $f (x) = 5 \sqrt[3]{x}$ then rewrite as $f (x) = 5 x^{\frac{1}{3}}$ and integrate
Functions involving fractions with denominators in terms of $x$ will need to be rewritten as negative powers of $x$ first
- e.g. If $f (x) = \frac{4}{x^{2}} + x^{2}$ then rewrite as $f (x) = 4 x^{- 2} + x^{2}$ and integrate

The formulae for integrating powers of $x$ apply to all rational numbers so it is possible to integrate any expression that is a sum or difference of powers of $x$
- e.g. If $f (x) = 8 x^{3} - 2 x + 4$ then $\int f (x) d x = \frac{8 x^{3 + 1}}{3 + 1} - \frac{2 x^{1 + 1}}{1 + 1} + 4 x + c = 2 x^{4} - x^{2} + 4 x + c$
Products and quotients cannot be integrated this way so would need expanding/simplifying first
- e.g. If $f (x) = 8 x^{2} (2 x - 3)$ then $\int f (x) d x = \int (16 x^{3} - 24 x^{2}) d x = \frac{16 x^{4}}{4} - \frac{24 x^{3}}{3} + c = 4 x^{4} - 8 x^{3} + c$

You can speed up the process of integration in the exam by committing the pattern of basic integration to memory
- In general you can think of it as 'raising the power by one and dividing by the new power'
- Practice this lots before your exam so that it comes quickly and naturally when doing more complicated integration questions

Given that

$\frac{d y}{d x} = 3 x^{4} - 2 x^{2} + 3 - \frac{1}{\sqrt{x}}$

find an expression for $y$ in terms of $x$ .

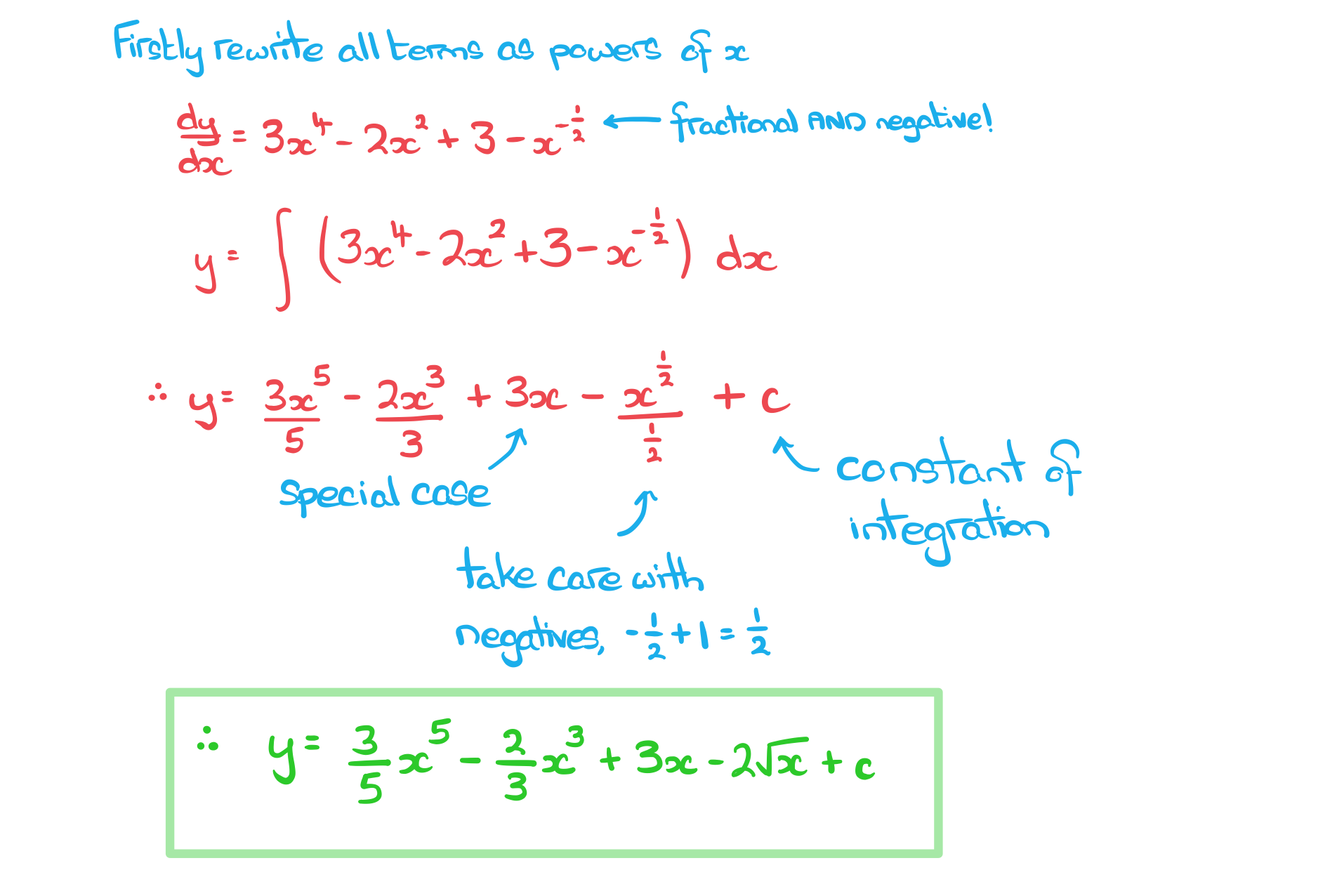
5-3-1-ib-sl-aa-version-we1-soltn