Bayes' Theorem

What is Bayes’ Theorem

Bayes’ Theorem allows you switch the order of conditional probabilities
- If you know $P (B)$ , $P (B')$ and $P (A | B)$ then Bayes’ Theorem allows you to find $P (B | A)$
Essentially if you have a tree diagram you will already know the conditional probabilities of the second branches
- Bayes’ Theorem allows you to find the conditional probabilities if you switch the order of the events
For any two events A and B Bayes’ Theorem states:

$P (B| A) = \frac{P (B) P (A | B)}{P (B) P (A | B) + P (B') P (A | B')}$

- This is given in the formula booklet
- This formula is derived using the formulae:
  - $P (B| A) = \frac{P (B \cap A)}{P (A)}$
  - $P (A) = P (B \cap A) + P (B' \cap A)$
  - $P (B \cap A) = P (B) P (A| B)$ and $P (B' \cap A) = P (B') P (A| B')$
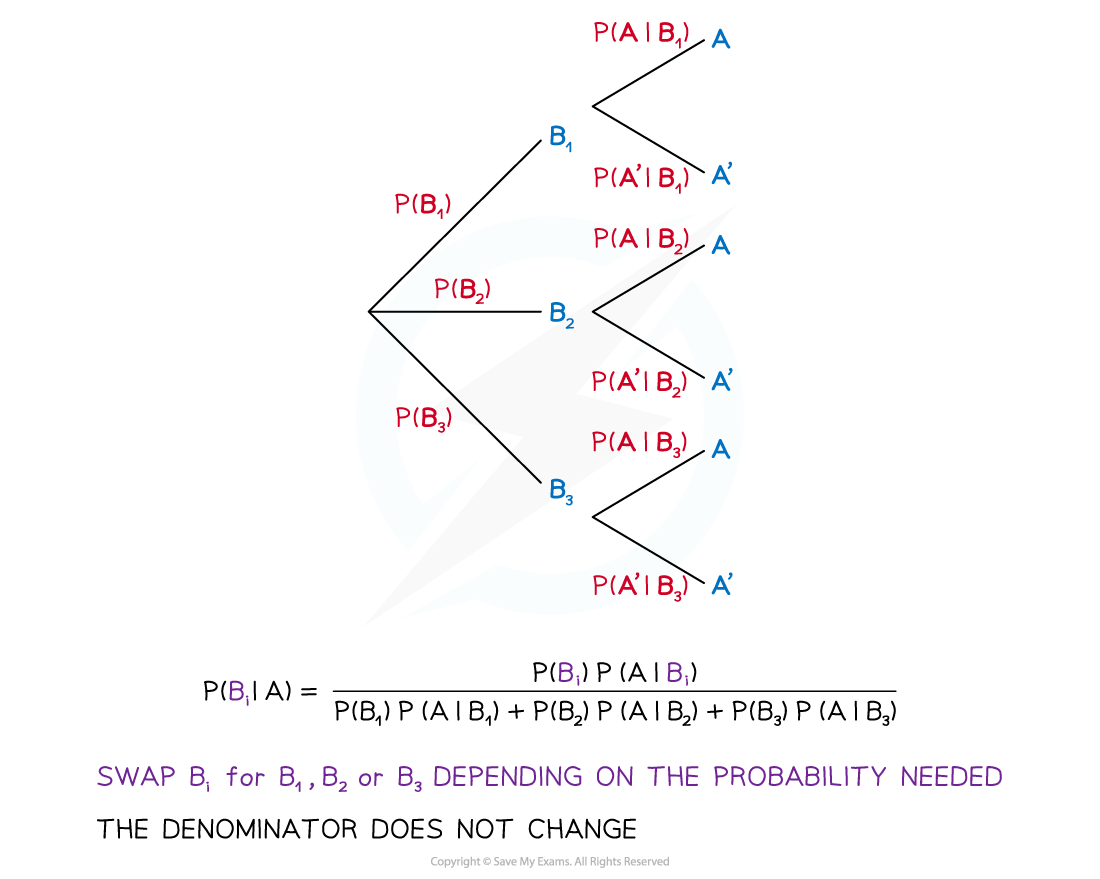
Bayes’ Theorem can be extended to mutually exclusive events B₁, B₂, ..., B_n and any other event A
- In your exam you will have a maximum of three mutually exclusive events

$P (B_{i}| A) = \frac{P (B_{i}) P (A | B_{i})}{P (B_{1}) P (A | B_{1}) + P (B_{2}) P (A | B_{2}) + P (B_{3}) P (A | B_{3})}$

This is given in the formula booklet

How do I calculate conditional probabilities using Bayes’ Theorem?

Start by drawing a tree diagram

Label B₁& B₂ (& B₃ if necessary) on the first set of branches
Label A & A’ on the second set of branches

The questions will give you enough information to label the probabilities on this tree
Identify the probabilities needed to use Bayes’ Theorem

The probabilities will come in pairs: $P (B_{i})$ and $P (A | B_{i})$

4-3-3-ib-aa-hl-bayes-theorem

Examiner Tip

In an exam you are less likely to make a mistake when using the formula if you draw a tree diagram first

Worked example

Lucy is doing a quiz. For each question there’s a 45% chance that it is about music, 30% chance that it is about TV and 25% chance that it is about literature. The probability that Lucy answers a question correctly is 0.6 for music, 0.95 for TV and 0.4 for literature.

Draw a tree diagram to represent this information.

4-3-3-ib-aa-hl-bayes-theorem-a-we-solution

Given that Lucy answered a question correctly, find the probability that it was about TV.

4-3-3-ib-aa-hl-bayes-theorem-b-we-solution

Bayes' Theorem (DP IB Maths: AA HL)

Revision Note

Bayes' Theorem

What is Bayes’ Theorem

How do I calculate conditional probabilities using Bayes’ Theorem?

Examiner Tip

Worked example

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Dan