Geometric Proof with Vectors (DP IB Maths: AA HL)

How can vectors be used to prove geometrical properties?

• If two vectors can be shown to be parallel then this can be used to prove parallel lines
• If two vectors are scalar multiples of each other then they are parallel
• To prove that two vectors are parallel simply show that one is a scalar multiple of the other
• If two vectors can be shown to be perpendicular then this can be used to prove perpendicular lines
• If the scalar product is zero then the two vectors are perpendicular
• If two vectors can be shown to have equal magnitude then this can be used to prove two lines are the same length 
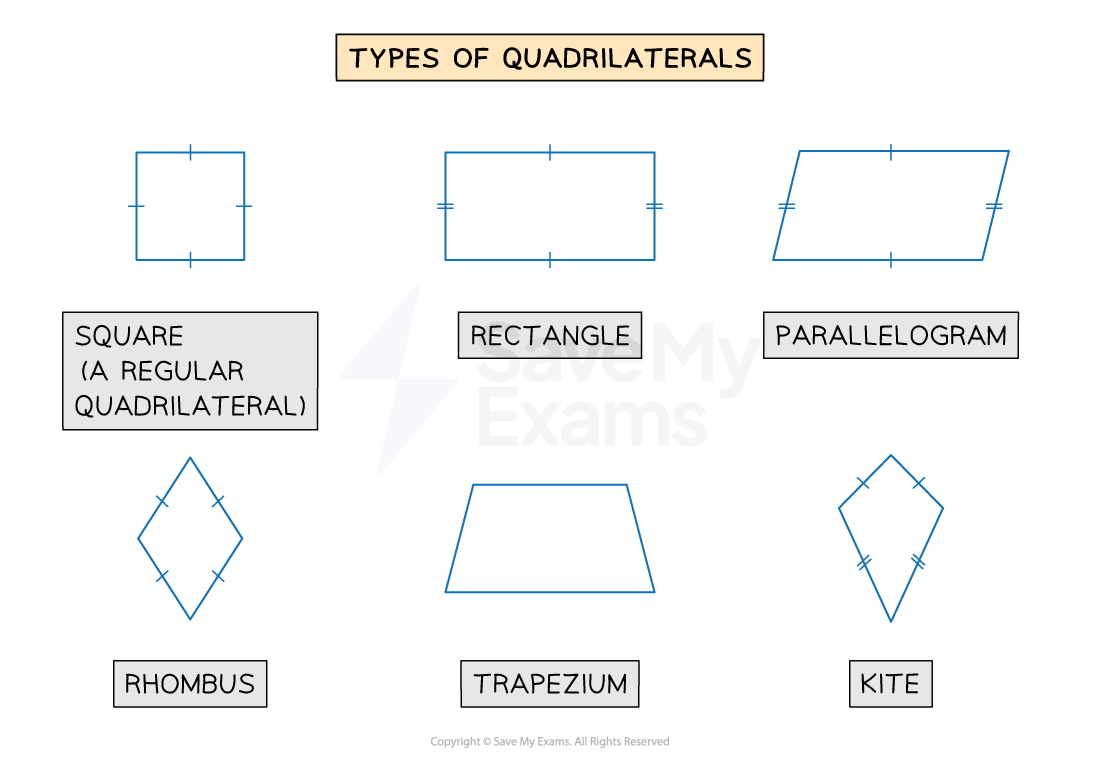
• To prove a 2D shape is a parallelogram vectors can be used to
• Show that there are two pairs of parallel sides
• Show that the opposite sides are of equal length
• The vectors opposite each other will be equal
• If the angle between two of the vectors is shown to be 90° then the parallelogram is a rectangle
• To prove a 2D shape is a rhombus vectors can be used to
• Show that there are two pairs of parallel sides
• The vectors opposite each other with be equal
• Show that all four sides are of equal length
• If the angle between two of the vectors is shown to be 90° then the rhombus is a square

How are vectors used to follow paths through a diagram?

• In a geometric diagram the vector  forms a path from the point A to the point B
• This is specific to the path AB
• If the vector  is labelled a then any other vector with the same magnitude and direction as a could also be labelled a
• The vector  would be labelled -a
• It is parallel to a but pointing in the opposite direction
• If the point M is exactly halfway between A and B it is called the midpoint of A and the vector could be labelled 
• If there is a point X on the line AB such that then X is two-thirds of the way along the line 
• Other ratios can be found in similar ways
• A diagram often helps to visualise this
• If a point X divides a line segment AB into the ratio p : q then
•  
•  

How can vectors be used to find the midpoint of two vectors?

• If the point A has position vector a and the point B has position vector b then the position vector of the midpoint of  is 
• The displacement vector 
• Let M be the midpoint of then 
• The position vector 

How can vectors be used to prove that three points are collinear?

• Three points are collinear if they all lie on the same line
• The vectors between the three points will be scalar multiples of each other
• The points A, B and C are collinear if 
• If the points A, B and M are collinear and  then M is the midpoint of