Position & Displacement Vectors (DP IB Maths: AA HL)

Revision Note

Author

Amber

Last updated

31 October 2023

Did this video help you?

Adding & Subtracting Vectors

How are vectors added and subtracted numerically?

To add or subtract vectors numerically simply add or subtract each of the corresponding components
In column vector notation just add the top, middle and bottom parts together

For example: $(\binom{2}{\begin{matrix} 1 \\ - 5 \end{matrix}}) - (\binom{1}{\begin{matrix} 4 \\ 3 \end{matrix}}) = (\binom{1}{\begin{matrix} - 3 \\ - 8 \end{matrix}})$

In base vector notation add each of the i, j, and k components together separately

For example: (2i + j – 5k) – (i + 4j + 3k) = (i – 3j – 8k)

Vector Addition Diagram 1b

How are vectors added and subtracted geometrically?

Vectors can be added geometrically by joining the end of one vector to the start of the next one
The resultant vector will be the shortest route from the start of the first vector to the end of the second

A resultant vector is a vector that results from adding or subtracting two or more vectors

If the two vectors have the same starting position, the second vector can be translated to the end of the first vector to find the resultant vector

This results in a parallelogram with the resultant vector as the diagonal

To subtract vectors, consider this as adding on the negative vector

For example: a – b = a + (-b)
The end of the resultant vector a – b will not be anywhere near the end of the vector b

Instead, it will be at the point where the end of the vector -b would be

Examiner Tip

Working in column vectors tends to be easiest when adding and subtracting
- in your exam, it can help to convert any vectors into column vectors before carrying out calculations with them
If there is no diagram, drawing one can be helpful to help you visualise the problem

Worked example

Find the resultant of the vectors a = 5i – 2j and b = $(\binom{- 3}{\begin{matrix} 1 \\ 2 \end{matrix}})$ .

3-9-2-ib-aa-hl-add--sub-vectors-we-solution-a-

Did this video help you?

Position Vectors

What is a position vector?

A position vector describes the position of a point in relation to the origin

It describes the direction and the distance from the point O: 0i + 0j + 0k or $(\binom{0}{\begin{matrix} 0 \\ 0 \end{matrix}})$
It is different to a displacement vector which describes the direction and distance between any two points

The position vector of point A is written with the notation a = $\vec{OA}$

The origin is always denoted O

The individual components of a position vector are the coordinates of its end point

For example the point with coordinates (3, -2, -1) has position vector 3i – 2j – k

Worked example

Determine the position vector of the point with coordinates (4, -1, 8).

3-9-2-ib-aa-hl-position-vector-we-solution

Did this video help you?

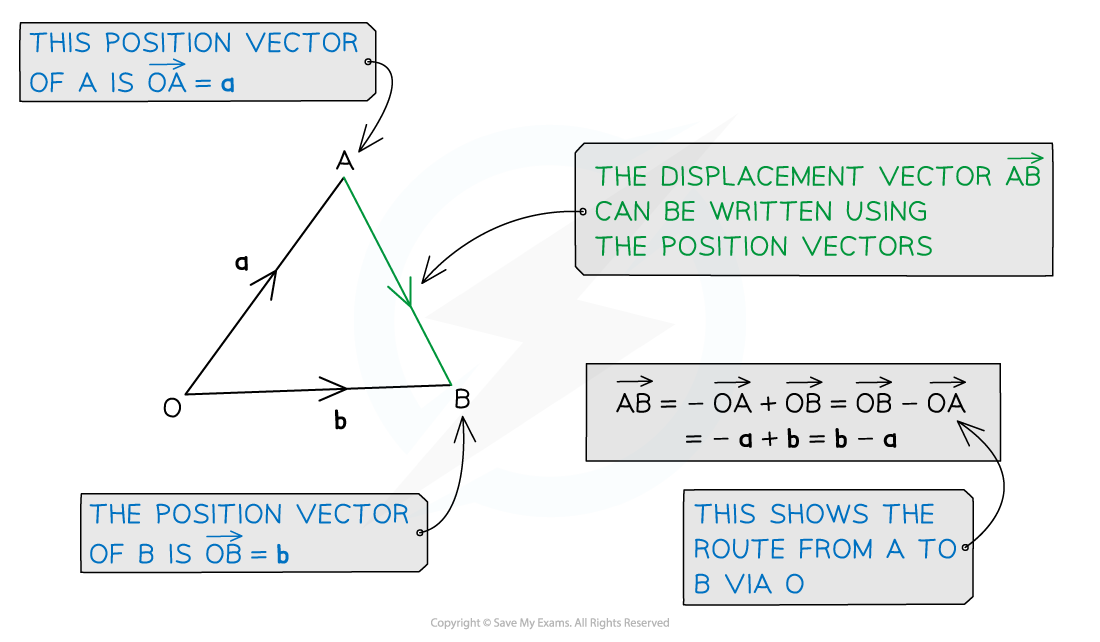
Displacement Vectors

What is a displacement vector?

A displacement vector describes the shortest route between any two points
- It describes the direction and the distance between any two points
- It is different to a position vector which describes the direction and distance from the point O: 0i + 0j or $(\binom{0}{0})$
The displacement vector of point B from the point A is written with the notation $\vec{AB}$
A displacement vector between two points can be written in terms of the displacement vectors of a third point
- $\vec{AB} = \vec{AC} + \vec{CB}$
A displacement vector can be written in terms of its position vectors
- For example the displacement vector $\vec{AB}$ can be written in terms of $\vec{OA}$ and $\vec{OB}$
- $\vec{AB} = \vec{AO} + \vec{OB} = - \vec{OA} + \vec{OB} = \vec{OB} - \vec{OA}$
- For position vector a = $\vec{OA}$ and b = $\vec{OB}$ the displacement vector $\vec{AB}$ can be written b – a

Examiner Tip

In an exam, sketching a quick diagram can help to make working out a displacement vector easier

Worked example

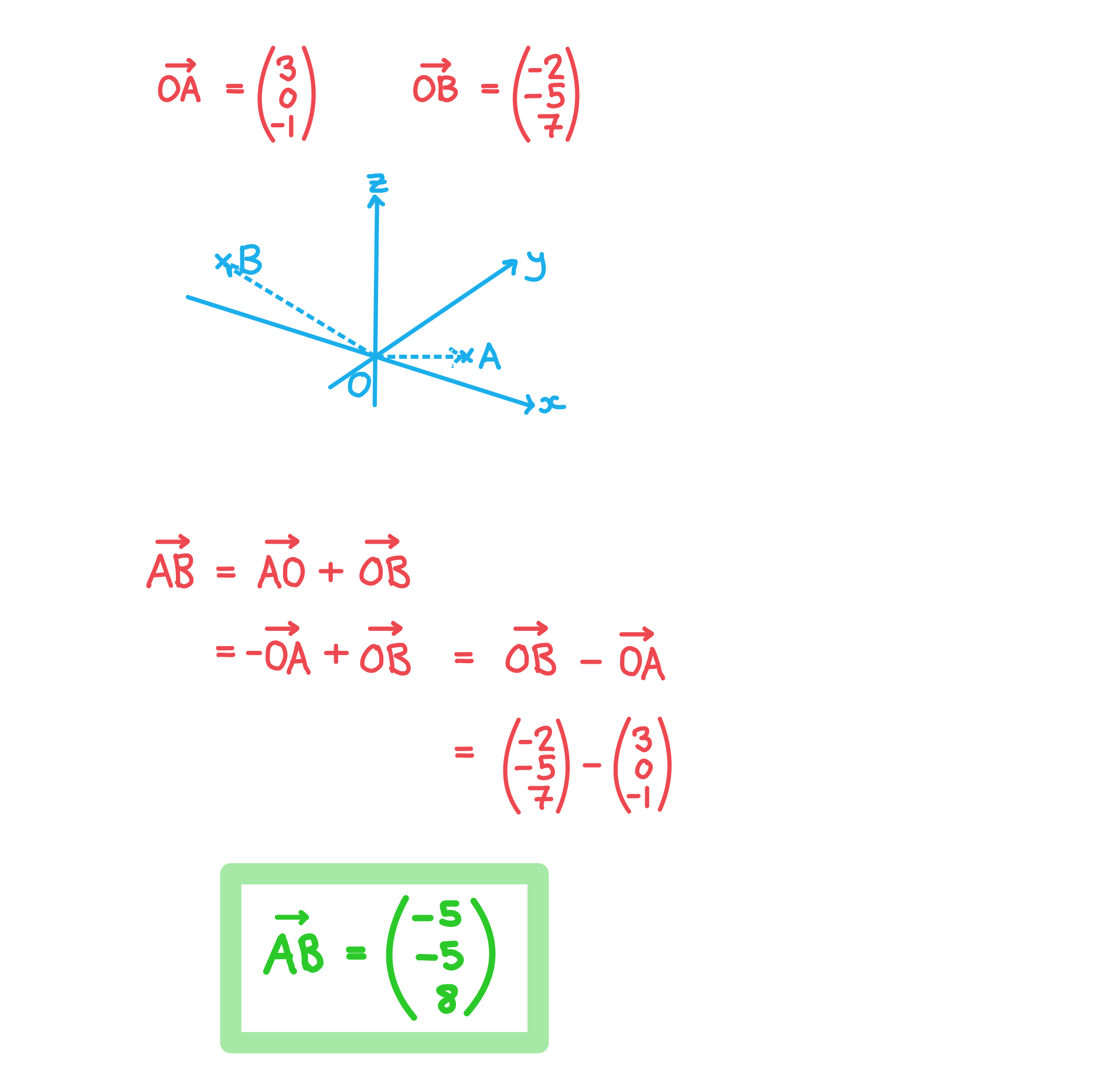
The point A has coordinates (3, 0, -1) and the point B has coordinates (-2, -5, 7). Find the displacement vector $\vec{AB}$ .

3-9-2-vectors-we-solution-position-and-displacement-wqe-solution

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself Flashcards

Did this page help you?

Previous:3.9.1 Introduction to VectorsNext:3.9.3 Magnitude of a Vector

Position & Displacement Vectors (DP IB Maths: AA HL)

Revision Note

How are vectors added and subtracted numerically?

How are vectors added and subtracted geometrically?

What is a position vector?

What is a displacement vector?

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

1. Number & Algebra

1.1 Number & Algebra Toolkit

1.1.1 Standard Form

1.1.2 Laws of Indices

1.1.3 Partial Fractions

1.2 Exponentials & Logs

1.2.1 Introduction to Logarithms

1.2.2 Laws of Logarithms

1.2.3 Solving Exponential Equations

1.3 Sequences & Series

1.3.1 Language of Sequences & Series

1.3.2 Arithmetic Sequences & Series

1.3.3 Geometric Sequences & Series

1.3.4 Applications of Sequences & Series

1.3.5 Compound Interest & Depreciation

1.4 Simple Proof & Reasoning

1.4.1 Proof

1.5 Further Proof & Reasoning

1.5.1 Proof by Induction

1.5.2 Proof by Contradiction

1.6 Binomial Theorem

1.6.1 Binomial Theorem

1.6.2 Extension of The Binomial Theorem

1.7 Permutations & Combinations

1.7.1 Counting Principles

1.7.2 Permutations & Combinations

1.8 Complex Numbers

1.8.1 Intro to Complex Numbers

1.8.2 Modulus & Argument

1.8.3 Introduction to Argand Diagrams

1.9 Further Complex Numbers

1.9.1 Geometry of Complex Numbers

1.9.2 Forms of Complex Numbers

1.9.3 Complex Roots of Polynomials

1.9.4 De Moivre's Theorem

1.9.5 Roots of Complex Numbers

1.10 Systems of Linear Equations

1.10.1 Systems of Linear Equations

1.10.2 Algebraic Solutions

2. Functions

2.1 Linear Functions & Graphs

2.1.1 Equations of a Straight Line

2.2 Quadratic Functions & Graphs

2.2.1 Quadratic Functions

2.2.2 Factorising & Completing the Square

2.2.3 Solving Quadratics

2.2.4 Quadratic Inequalities

2.2.5 Discriminants

2.3 Functions Toolkit

2.3.1 Language of Functions

2.3.2 Composite & Inverse Functions

2.3.3 Symmetry of Functions

2.3.4 Graphing Functions

2.4 Other Functions & Graphs

2.4.1 Exponential & Logarithmic Functions

2.4.2 Solving Equations

2.4.3 Modelling with Functions

2.5 Reciprocal & Rational Functions

2.5.1 Reciprocal & Rational Functions

2.6 Transformations of Graphs

2.6.1 Translations of Graphs

2.6.2 Reflections of Graphs

2.6.3 Stretches Graphs

2.6.4 Composite Transformations of Graphs

2.7 Polynomial Functions

2.7.1 Factor & Remainder Theorem

2.7.2 Polynomial Division

2.7.3 Polynomial Functions

2.7.4 Roots of Polynomials

2.8 Inequalities

2.8.1 Solving Inequalities Graphically