Reciprocal & Rational Functions (DP IB Analysis & Approaches (AA)): Revision Note
Did this video help you?
Reciprocal functions & graphs
What is the reciprocal function?
The reciprocal function is defined by
Its domain is the set of all real values except 0
Its range is the set of all real values except 0
The reciprocal function has a self-inverse nature
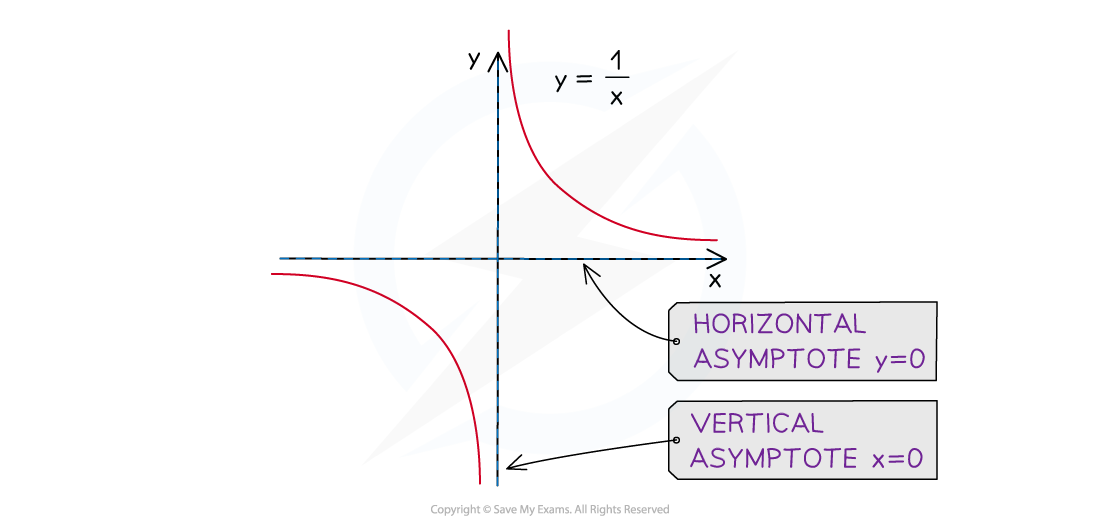
What are the key features of the reciprocal graph?
The graph does not have a y-intercept
The graph does not have any roots
The graph has two asymptotes
A horizontal asymptote at the x-axis:
This is the limiting value when the absolute value of x gets very large
A vertical asymptote at the y-axis:
This is the value that causes the denominator to be zero
The graph has two axes of symmetry
The graph does not have any minimum or maximum points
Did this video help you?
Linear rational functions & graphs
What is a rational function with linear expressions?
A (linear) rational function is of the form
e.g.
The reciprocal function is a special case of a rational function
The inverse is also a rational function
You do not need to remember this formula
You can derive the inverse easily in your exam
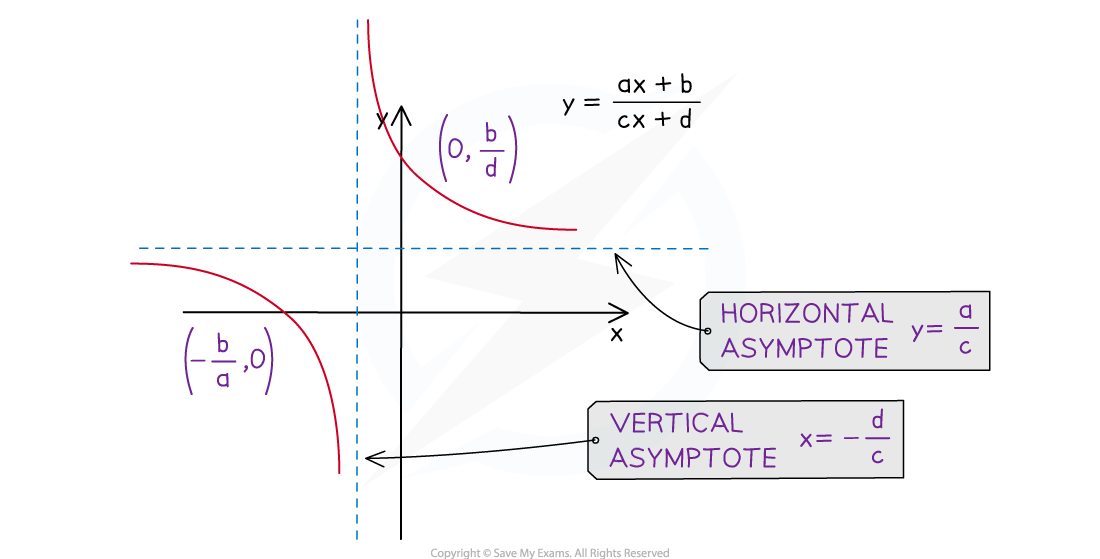
What are the key features of linear rational graphs?
Intersections with coordinate axes
The graph has a y-intercept at
provided
Substitute
to find the y-coordinate
e.g. the y-intercept of
is
e.g.
does not have a y-intercept
The graph has one root at
provided
Set the numerator equal to zero and solve
e.g. the root of
is
e.g.
does not have any roots
Asymptotes
The graph has two asymptotes
A horizontal asymptote:
This is the limiting value when the absolute value of x gets very large
e.g. the horizontal asymptote of
is
A vertical asymptote:
This is the value that causes the denominator to be zero
e.g. the horizontal asymptote of
is
Domain and range
Its domain is the set of all real values except
It is undefined for the value of
which causes the denominator to equal zero
e.g. the domain of
is
Its range is the set of all real values except
e.g. the range of
is
Turning points
The graph does not have any minimum or maximum points
Examiner Tips and Tricks
If you are asked to sketch or draw a rational graph:
Give the coordinates of any intercepts with the axes
Give the equations of the asymptotes
Worked Example
The function is defined by
for
.
a) Write down the equation of
(i) the vertical asymptote of the graph of ,
(ii) the horizontal asymptote of the graph of .
Answer:

b) Find the coordinates of the intercepts of the graph of with the axes.
Answer:
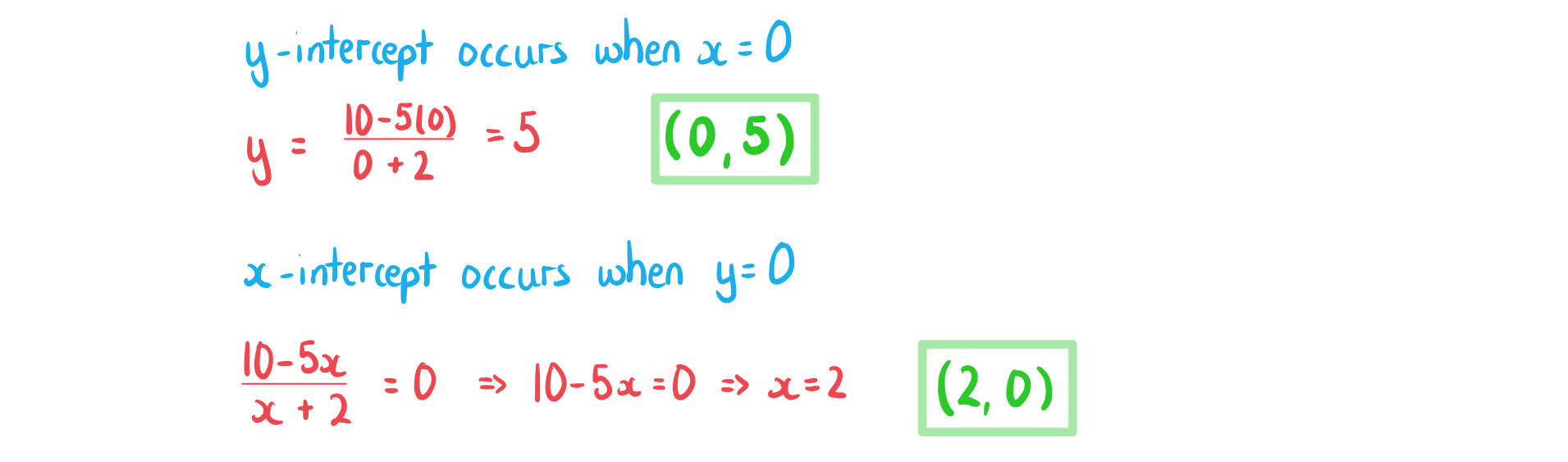
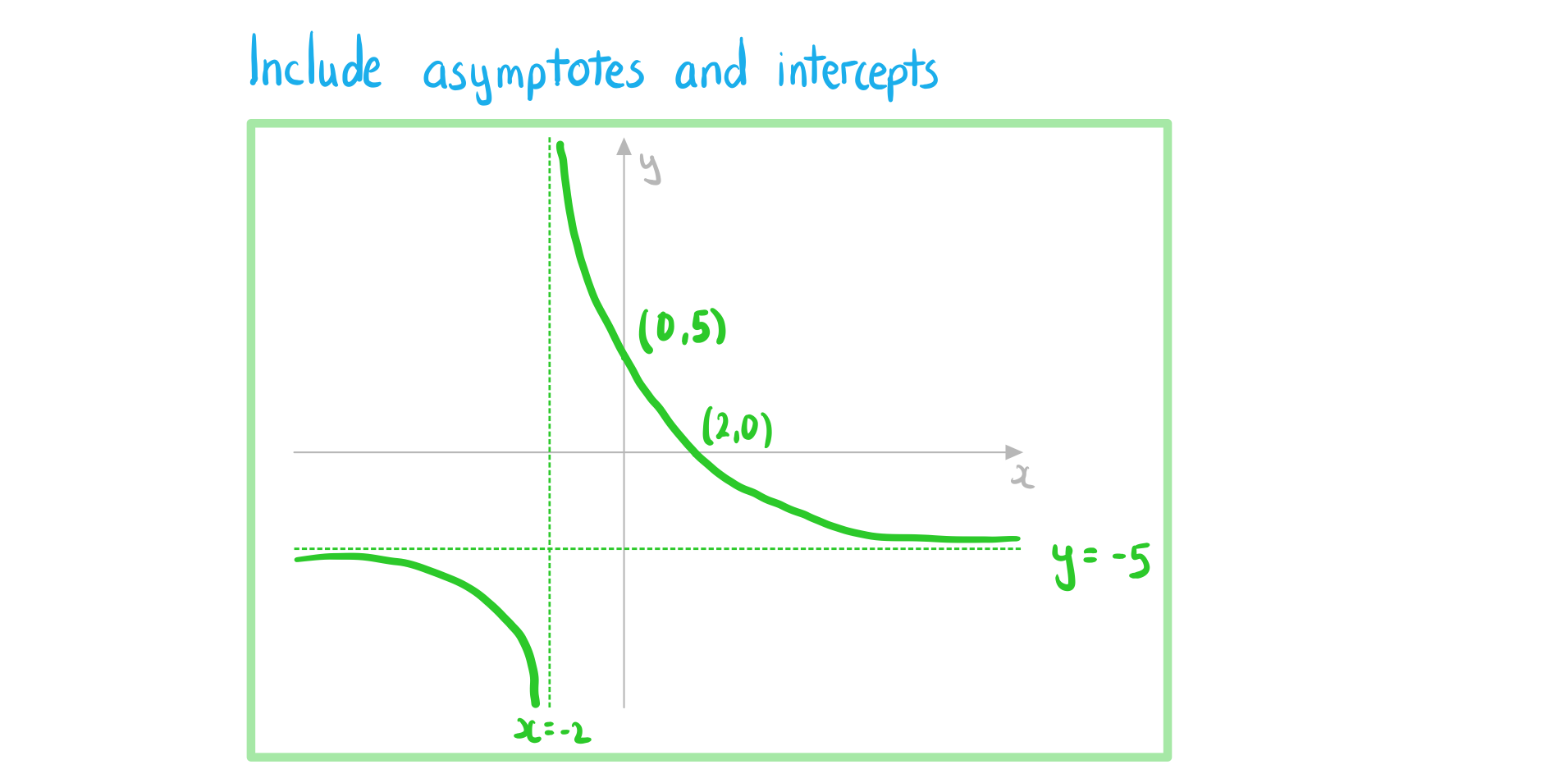
c) Sketch the graph of .
Answer:

Unlock more, it's free!
Did this page help you?