Exact Values (DP IB Analysis & Approaches (AA)): Revision Note

Trigonometry exact values

What are exact values in trigonometry?

• For certain angles the values of sin θ, cos θ and tan θ can be written exactly

  • This means using fractions and surds

  • You should be familiar with these values and be able to derive the values using geometry

• You are expected to know the exact values of sin, cos and tan for angles of 0°, 30°, 45°, 60°, 90°, 180° and their multiples

  • In radians this is and their multiples

• The exact values you are expected to know are:

How do I find the exact values of other angles?

• Use the symmetries of the unit circle

• You can use this to find the exact trig values for any multiple of 30° or 45°

  • For example:

    • 

    • 

    • 

How do I derive the exact values in trigonometry?

• There are two special right-triangles that can be used to derive the exact values

30° - 60° - 90°

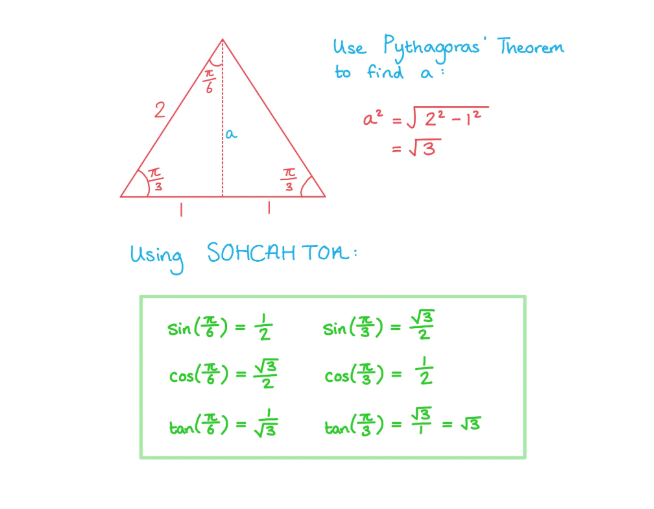
• Draw an equilateral triangle where each side has length 2

• Split the triangle into two identical triangles

• Looking at one triangle:

  • One side has length 1

  • The hypotenuse has length 2

  • The other side has length √3

45° - 45° - 90°

• Draw a right-angled isosceles triangle where two sides have length 1

• The third side has length √2