Revision NotesExam QuestionsFlashcards
IBMaths: AA HLDPRevision Notes3. Geometry & Trigonometry3.2 Geometry of 3D Shapes3.2.2 Volume & Surface Area

Volume & Surface Area (DP IB Maths: AA HL)

Revision Note

Amber

Author

Amber

Last updated

Did this video help you?

Volume of 3D Shapes

What is volume?

  • The volume of a 3D shape is a measure of how much 3D space it takes up
    • A 3D shape is also called a solid
  • You need to be able to calculate the volume of a number of common shapes

 

How do I find the volume of cuboids, prisms and cylinders?

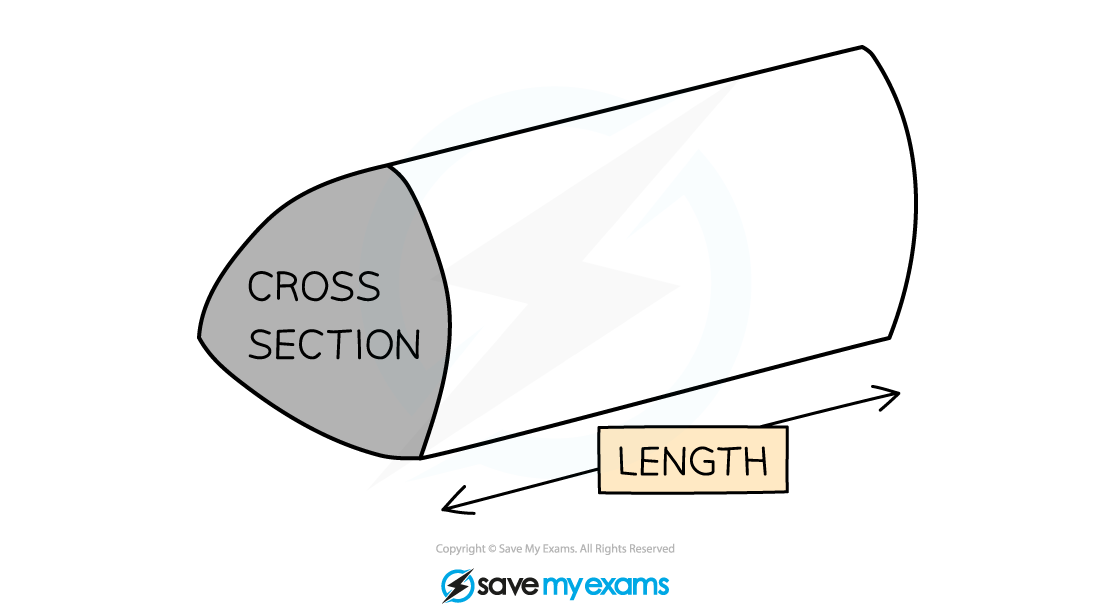
  • A prism is a 3-D shape that has two identical base shapes connected by parallel edges
    • A prism has the same base shape all the way through
    • A prism takes its name from its base
  • To find the volume of any prism use the formula:

Volume of a prism = Ah

    • Where A is the area of the cross section and h is the base height
      • h could also be the length of the prism, depending on how it is oriented
    • This is in the formula booklet in the prior learning section at the beginning
    • The base could be any shape so as long as you know its area and length you can calculate the volume of any prism

Prism volume

  • Note two special cases:
    • To find the volume of a cuboid use the formula:

begin mathsize 22px style table attributes columnalign right center left columnspacing 0px end attributes row cell Volume space of space straight a space cuboid space end cell equals cell space length space cross times space width space cross times space height end cell row cell V space end cell equals cell space l w h end cell end table end style

    • The volume of a cylinder can be found in the same way as a prism using the formula:

begin mathsize 22px style Volume space of space straight a space cylinder space equals space pi italic space r to the power of italic 2 italic space h end style

    • where r is the radius, h is the height (or length, depending on the orientation
    • Note that a cylinder is technically not a prism as its base is not a polygon, however the method for finding its volume is the same
  • Both of these are in the formula booklet in the prior learning section

How do I find the volume of pyramids and cones?

  • In a right-pyramid the apex (the joining point of the triangular faces) is vertically above the centre of the base
    • The base can be any shape but is usually a square, rectangle or triangle
  • To calculate the volume of a right-pyramid use the formula

V equals 1 third A h

    • Where A is the area of the base, h is the height
    • Note that the height must be vertical to the base
  • A right cone is a circular-based pyramid with the vertical height joining the apex to the centre of the circular base
  • To calculate the volume of a right-cone use the formula

V equals 1 third pi space r to the power of 2 space end exponent h

    • Where r is the radius, h is the height
  • These formulae are both given in the formula booklet

 

How do I find the volume of a sphere?

  • To calculate the volume of a sphere use the formula

V equals 4 over 3 pi space r cubed

    • Where r is the radius
      • the line segment from the centre of the sphere to the surface
    • This formula is given in the formula booklet

Examiner Tip

  • Remember to make use of the formula booklet in the exam as all the volume formulae you need will be here
    • Formulae for basic 3D objects (cuboid, cylinder and prism) are in the prior learning section
    • Formulae for other 3D objects (pyramid, cone and sphere) are in the Topic 3: Geometry section

Worked example

A dessert can be modelled as a right-cone of radius 3 cm and height 12 cm and a scoop of ice-cream in the shape of a sphere of radius 3 cm.  Find the total volume of the ice-cream and cone.

diagram-for-we-3-2-2

3-2-2-ai-sl-volume-we-solution

Did this video help you?

Surface Area of 3D Shapes

What is surface area?

  • The surface area of a 3D shape is the sum of the areas of all the faces that make up a shape
    • A face is one of the flat or curved surfaces that make up a 3D shape
    • It often helps to consider a 3D shape in the form of its 2D net

 

How do I find the surface area of cuboids, pyramids and prisms?

  • Any prisms and pyramids that have polygons as their bases have only flat faces
    • The surface area is simply found by adding up the areas of these flat faces
    • Drawing a 2D net will help to see which faces the 3D shape is made up of

How do I find the surface area of cylinders, cones and spheres?

  • Cones, cylinders and spheres all have curved faces so it is not always as easy to see their shape
    • The net of a cylinder is made up of two identical circles and a rectangle
    • The rectangle is the curved surface area and is harder to identify
    • The length of the rectangle is the same as the circumference of the circle
    • The area of the curved surface area is

begin mathsize 22px style A equals 2 pi r h end style

      • where r is the radius, h is the height
    • This is given in the formula book in the prior learning section
    • The area of the total surface area of a cylinder is

begin mathsize 22px style A equals 2 pi r h plus 2 pi r squared blank end style

    • This is not given in the formula book, however it is easy to put together as both the area of a circle and the area of the curved surface area are given
  • The net of a cone consists of the circular base along with the curved surface area
    • The area of the curved surface area is

begin mathsize 22px style A blank equals pi r l end style

      • Where r is the radius and l is the slant height
    • This is given in the formula book
      • Be careful not to confuse the slant height, l, with the vertical height, h
      • Note that r, h and l will create a right-triangle with l as the hypotenuse
    • The area of the total surface area of a cone is

begin mathsize 22px style A equals pi r l plus pi r squared blank end style

    • This is not given in the formula book, however it is easy to put together as both the area of a circle and the area of the curved surface area are given
  • To find the surface area of a sphere use the formula

A equals 4 pi r squared

      • where r is the radius (line segment from the centre to the surface)
    • This is given in the formula booklet, you do not have to remember it

Examiner Tip

  • Remember to make use of the formula booklet in the exam as all the area formulae you need will be here
    • Formulae for basic 2D shapes (parallelogram, triangle, trapezoid, circle, curved surface of a cylinder) are in the prior learning section
    • Formulae for other 2D shapes (curved surface area of a cone and surface area of a sphere ) are in the Topic 3: Geometry section

Worked example

In the diagram below ABCD  is the square base of a right pyramid with vertex V .  The centre of the base is M. The sides of the square base are 3.6 cm and the vertical height is 8.2 cm.

sa-diagram-for-we-3-2-2

i)
Use the Pythagorean Theorem to find the distance VN.

 3-2-2-ai-sl-surface-area-we-solution-i

ii)
Calculate the area of the triangle ABV.

 3-2-2-ai-sl-surface-area-we-solution-ii

iii)
Find the surface area of the right pyramid.

3-2-2-ai-sl-surface-area-we-solution-iii

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfFlashcards

    Did this page help you?

    Previous:3.2.1 3D Coordinate GeometryNext:3.3.1 Pythagoras & Right-Angled Trigonometry
    Amber

    Author: Amber

    Expertise: Maths

    Amber gained a first class degree in Mathematics & Meteorology from the University of Reading before training to become a teacher. She is passionate about teaching, having spent 8 years teaching GCSE and A Level Mathematics both in the UK and internationally. Amber loves creating bright and informative resources to help students reach their potential.