Modelling with Functions (DP IB Analysis & Approaches (AA)): Revision Note
Did this video help you?
Modelling with Functions
What is a mathematical model?
A mathematical model simplifies a real-world situation so it can be described using mathematics
The model can then be used to make predictions
Assumptions about the situation are made in order to simplify the mathematics
Models can be refined (improved) if further information is available or if the model is compared to real-world data
How do I set up the model?
The question could:
give you the equation of the model
tell you about the relationship
It might say the relationship is linear, quadratic, etc
ask you to suggest a suitable model
Use your knowledge of each model
E.g. if it is compound interest then an exponential model is the most appropriate
You may have to determine a reasonable domain
Consider real-life context
E.g. if dealing with hours in a day then
E.g. if dealing with physical quantities (such as length) then,
Consider the possible ranges
If the outcome cannot be negative then you want to choose a domain which corresponds to a range with no negative values
Sketching the graph is helpful to determine a suitable domain
Which models might I need to use?
You could be given any model and be expected to use it
Common models and examples include:
Linear
Arithmetic sequences
Linear regression
Quadratic
Projectile motion
The height of a cable supporting a bridge
Profit
Exponential
Geometric sequences
Exponential growth and decay
Compound interest
Logarithmic
Richter scale for the magnitude of earthquakes
Rational
Temperature of a cup of coffee
Trigonometric
The depth of a tide
How do I use a model?
You can use a model by substituting in values for the variable to estimate outputs
For example: Let
be the height of a football
seconds after being kicked
will be an estimate for the height of the ball 3 seconds after being kicked
Given an output you can form an equation with the model to estimate the input
For example: Let
be the profit made by selling
items
Solving
will give you an estimate for the number of items needing to be sold to make a profit of 100
If your variable is time then substituting
will give you the initial value according to the model
Fully understand the units for the variables
If the units of
are measured in thousand dollars then
represents $3000
Look out for key words such as:
Initially
This means
Minimum/maximum
Limiting value
This means
gets large
What do I do if some of the parameters are unknown?
A general method is to form equations by substituting in given values
You can form multiple equations and solve them simultaneously using your GDC
This method works for all models
For example, suppose
is the mass in kg after
hours
If you are told that the mass is 7 kg after 2 hours
Use
to find the value of
The initial value is the value of the function when the variable is 0
This is normally one of the parameters in the equation of the model
Worked Example
The temperature, °C, of a cup of coffee is monitored. Initially the temperature is 80°C and 5 minutes later it is 40°C . It is suggested that the temperature follows the model:
.
where is the time, in minutes, after the coffee has been made.
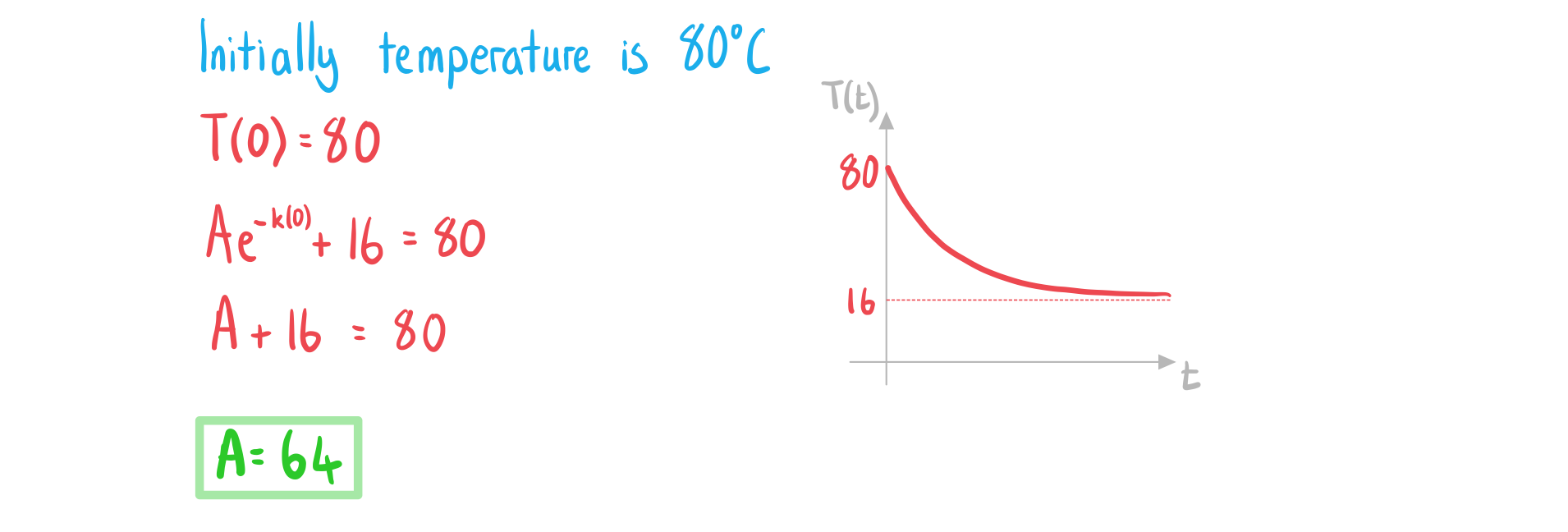
a) State the value of .
Answer:
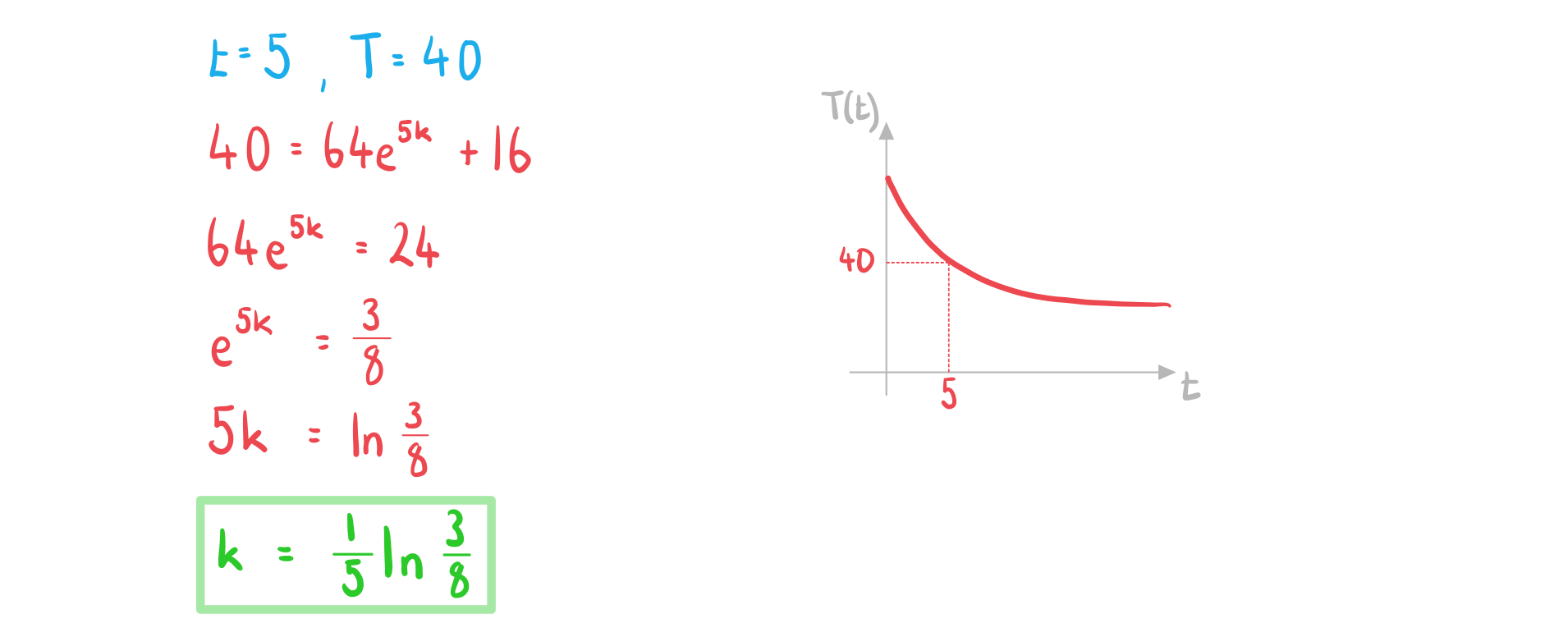
b) Find the exact value of .
Answer:
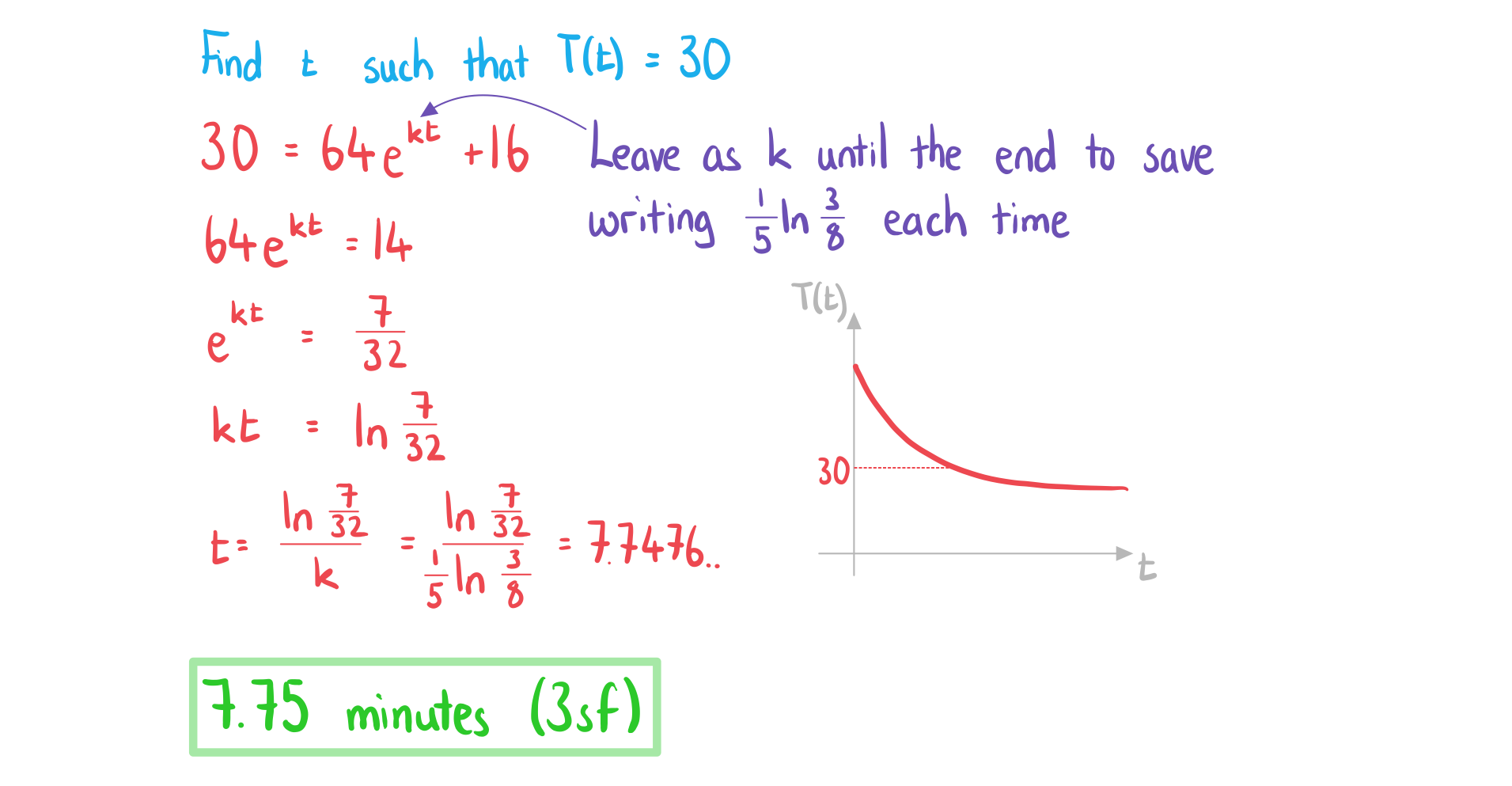
c) Find the time taken for the temperature of the coffee to reach 30°C.
Answer:

Unlock more, it's free!
Did this page help you?